Метод узловых напряжений для схем с двумя узлами

Для сложных электрических цепей с двумя узлами система уравнений (1.24) вырождается в одно уравнение, из которого можно напрямую определить величину узлового напряжения:

Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками^[1].

В Международной системе единиц (СИ) ёмкость измеряется в фарадах, в системе СГС — в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

{\displaystyle C={\frac {Q}{\varphi }},}

где {\displaystyle Q} — заряд, {\displaystyle \varphi } — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):

{\displaystyle C=4\pi \varepsilon _{0}\varepsilon _{r}R,}

где ε₀ — электрическая постоянная, равная 8,854·10⁻¹² Ф/м, ε_r — относительная диэлектрическая проницаемость.

Вывод формулы[показать]

Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектрикомили вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

{\displaystyle C=\varepsilon _{0}\varepsilon _{r}{\frac {S}{d}},}

где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε_r — относительная диэлектрическая проницаемость среды между обкладками.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические зарядыи на тела, обладающие магнитным моментом, независимо от состояния ихдвижения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции {\displaystyle \mathbf {B} } (вектор индукции магнитного поля)^[3]. С математической точки зрения {\displaystyle \mathbf {B} =\mathbf {B} (x,y,z)} — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

· Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции{\displaystyle \mathbf {B} ,} а вектор напряжённости магнитного поля {\displaystyle \mathbf {H} }, что формально можно сделать, так как в вакууме эти два вектора совпадают^[4]; однако в магнитной среде вектор {\displaystyle \mathbf {H} } не несет уже того же физического смысла^[5], являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно {\displaystyle \mathbf {B} .}

Магнитное поле можно назвать особым видом материи^[6], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности свет и все другие электромагнитные волны.

Электрический ток(I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника.

· С точки зрения квантовой теории поля магнитное взаимодействие — как частный случай электромагнитного взаимодействия переносится фундаментальным безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля), часто (например, во всех случаях статических полей) — виртуальным.

мммммм

· цилиндрическая катушка индуктивности — цилиндрическая катушка Катушка индуктивности без магнитного сердечника, обмотка которой имеет форму цилиндра. [ГОСТ 20718 75] Тематики катушки индуктивности аппаратуры связи Синонимы цилиндрическая катушка EN cylindrical inductance coil FR bobine … Справочник технического переводчика

· цилиндрическая катушка индуктивности с сердечником — Катушка индуктивности, сердечник которой имеет форму цилиндра. [ГОСТ 20718 75] Тематики катушки индуктивности аппаратуры связи EN cylindrical cored coil FR bobine cylindrique á noyau … Справочник технического переводчика

· Цилиндрическая катушка индуктивности — 11. Цилиндрическая катушка индуктивности Цилиндрическая катушка Е. Cylindrical inductance coil F. Bobine cylindrique Источник: ГОСТ 20718 75: Катушки индуктивности аппаратуры связи. Термины и определения … Словарь-справочник терминов нормативно-технической документации

· Цилиндрическая катушка индуктивности с сердечником — 9. Цилиндрическая катушка индуктивности с сердечником Е. Cylindrical cored coil F. Bobine cylindrique à noyau Источник: ГОСТ 20718 75: Катушки индуктивности аппаратуры связи. Термины и определения … Словарь-справочник терминов нормативно-технической документации

· КАТУШКА ИНДУКТИВНОСТИ — индуктивная катушка, катушка из провода с изолир. витками; обладает значит. индуктивностью при относительно малых ёмкости и активном сопротивлении. К. и. изготовляют обычно из изолир. провода, наматываемого на каркас, к рый для увеличения… … Большой энциклопедический политехнический словарь

· катушка индуктивности — катушка из провода с изолированными витками; обладает значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Применяется в качестве одного из основных элементов электрических фильтров и колебательных контуров,… … Энциклопедический словарь

· тороидальная катушка — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN toroidal coil … Справочник технического переводчика

· тороидальная катушка — toroidinė ritė statusas T sritis automatika atitikmenys: angl. toroidal coil vok. Ringspule, f; Toroidspule, f rus. тороидальная катушка, f pranc. bobine toroïdale, f … Automatikos terminų žodynas

· тороидальная катушка — toroidinė ritė statusas T sritis fizika atitikmenys: angl. doughnut coil; toroidal coil vok. Toroidspule, f rus. тороидальная катушка, f pranc. bobine torique, f; bobine toroïdale, f … Fizikos terminų žodynas

· КАТУШКА ИНДУКТИВНОСТИ — индуктивная катушка, катушка из провода с изолир. витками; обладает значит. индуктивностью при относительно малых ёмкости и активном сопротивлении. К. и. изготовляют обычно из изолир. провода, наматываемого на каркас, к рый для увеличения… … Большой энциклопедический

· Магнитное поле –одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорциональной заряду частицы и ее скорости.

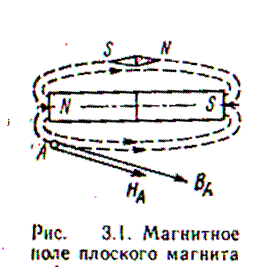· Магнитное поле изображается силовыми линиями, касательные к которым совпадают с ориентацией магнитных стрелок, внесенных в поле (рис. 3.1). Таким образом, магнитные стрелки как бы являются пробными элементами для магнитного поля.

· За положительное направление магнитного

· поля условно принимают направление

· северного полюса магнитной стрелки.

· Можно утверждать, что магнитное поле

· и электрический ток — взаимосвязанные явления.

· Магнитная индукция В —

· векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля. Эта характеристика является основной характеристикой магнитного поля, так как определяет электромагнитную силу, а также ЭДС индукции в проводнике, перемещающемся в магнитном поле.

· Единицей магнитной индукции является вебер, деленный на квадратный метр, или тесла (Тл):

· [В] =1Вб/1 м²= 1 Тл.

· Абсолютная магнитная проницаемость среды μ_a — величина, являющаяся коэффициентом, отражающим магнитные свойства среды:

·

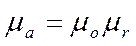
· где μ₀= 4π*10^-7(Ом*с)/м — магнитная постоянная, характеризующая магнитные свойства вакуума.

· Единицу Ом*секунда (Ом*с) называют генри (Гн) Таким образом, [μ₀]=Гн/м.

· Величину μ_r, называют относительной магнитной проницаемостью среды. Она показывает, во сколько раз индукция поля, созданного током в данной среде, больше или меньше, чем в вакууме, и является безразмерной величиной.

·

· Для большинства материалов проницаемость μ_r постоянна и близка к единице. Для ферромагнитных материалов μ_r является функцией тока, создающего магнитное поле, и достигает больших значений (10²-10⁵).

· Напряженность магнитного поля Н — векторная величина, которая не зависит от свойств среды и определяется только токами в проводниках, создающими магнитное поле.

· точке поля (точка А) к силовой линии. Напряженность связана с магнитной индукцией соотношением

·

·

· Единица напряженности магнитного поля — ампер на метр:

· [Н] =1А / 1 м

· Приведенные характеристики магнитного поля

· являются основными.

· Теперь рассмотрим производные характеристики.

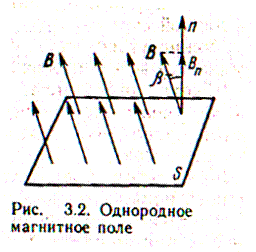
· Магнитный поток Ф — поток магнитной индукции.

· На рисунке 3.2 показано однородное магнитное

· поле, пересекающее площадку S. Магнитный поток Ф

· через площадку S в однородном магнитном поле

· равен произведению нормальной составляющей

· вектора индукции В_n на площадь S площадки:

· Ф=В_nS=BS cos β

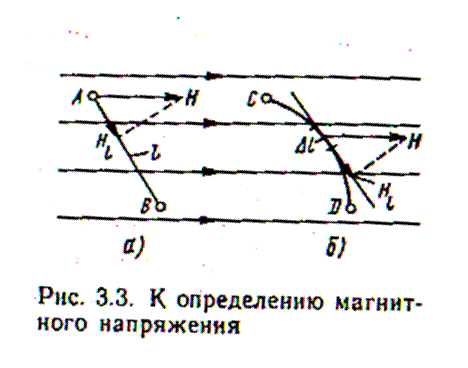· Магнитное напряжение (рисунок 3.3, а) в однородном магнитном поле определяется как произведение проекции H_ℓ вектора Н на отрезок АВ и длину этого отрезка ℓ:

·

·

·

·

·

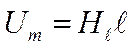
· В случае, когда поле неоднородно или участок, вдоль которого определяется U_m не прямолинейный, участок разбивается на элементарные участки Δℓ. Тогда в пределах малого участка Δℓ поле можно считать однородным, а участок прямолинейным.

·

·

·

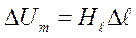
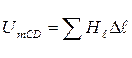
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы {\displaystyle d{\vec {F}}}, с которой магнитное поле действует на элемент объёма {\displaystyle dV} проводника с током плотности {\displaystyle {\vec {j}}}, находящегося в магнитном поле с индукцией {\displaystyle {\vec {B}}}, в Международной системе единиц (СИ) имеет вид:

{\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV}.

Если ток течёт по тонкому проводнику, то {\displaystyle {\vec {j}}dV=Id{\vec {l}}}, где {\displaystyle d{\vec {l}}} — «элемент длины» проводника — вектор, по модулю равный {\displaystyle dl} и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.

Здесь – сила Ампера, – сила тока в проводнике, – модуль вектора индукции магнитного поля, – длина участка проводника, на который воздействует магнитное поле, – угол между вектором индукции магнитного поля и направления тока.

Единица измерения силы – Н (ньютон).

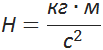
Сила Ампера — векторная величина. Сила Ампера принимает своё наибольшее значение когда векторы индукции и направления тока перпендикулярны ().

Направление силы ампера определяют по правилу лево

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамикедействует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью {\displaystyle \mathbf {v} } заряд {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического {\displaystyle \mathbf {E} } и магнитного {\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ)выражается как:

{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right)}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3