Интегрирование тригонометрических функций

Лекция 8. Интегрирование биноминальных дифференциалов. Разложение на простейшие дроби. Интегрирование тригонометрических функций.

Биноминальный дифференциал – это выражение вида , где

Теорема Чебышева

Интеграл

(1)

может быть выражен в элементарных функциях только в следующих трех случаях:

1) p – целое число. Тогда выражение 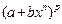развертывается по формуле бинома Ньютона и подынтегральная функция после раскрытия скобок будет суммой элементов вида , которые легко интегрируются.

2) целое число. Интеграл (1) приводится к интегралу от рациональной функции подстановкой 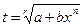, где r – знаменатель дроби p

3) целое число. Интеграл (1) приводится к интегралу от рациональной функции подстановкой , где r – знаменатель дроби p

Разложение на простейшие дроби. Общий случай.

Пусть , где P(x),Q(x) – многочлены.

Прежде всего заметим, что если степень m числителя P(x) больше или равна степени n знаменателя Q(x), то разделив многочлен P(x) на многочлен Q(x), получим в частном некоторый многочлен N(x) и в остатке многочлен не выше степени (n-1). Следовательно

Для N(x) – обычное интегрирование.

Дробь - правильная дробь.

Многочлен Q(x) может быть представлен в виде произведения линейных и квадратичных множителей с действительными коэффициентами:

, где

- к-кратный корень уравнения Q(x)=0, а квадратное уравнение имеет сопряженные комплексные корни , которые служат t-кратными сопряженными корнями уравнения Q(x)=0

Общая формула разложения дроби следующая:

(*)

Таким образом, интеграл от всякой рациональной дроби сводится к интегралам от простейших рациональных дробей, которые находятся достаточно легко.

Примеры

1. Получаем систему

Более простой метод:

При x=0, A=3. При x=1, B=-1. При x=-1, C=-2

Имеем тождество , тогда

2.

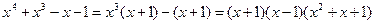
Разлагаем дробь на простейшие дроби:

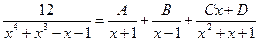Коэффициенты A,B,C,D находим из тождества

Подставляя последовательно x=0, x=1, x=-1, x=2 получим систему:

следовательно

=

3.

Получаем систему уравнений

Имеем =

Интеграл 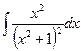вычислим применив правило интегрирования по частям

тогда

Окончательно исходный интеграл равен

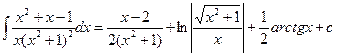
Интегрирование тригонометрических функций

Рассмотрим основные методы интегрирования тригонометрических функций

1. В приложениях математического анализа важное значение имеют интегралы вида Рассмотрим различные значения параметров m и n

a)Если хотя бы одно из m или n нечетное (m>0,n>0), то интеграл вычисляется непосредственно.

Пример

b)Если оба показателя четные числа (m>0,n>0), то используются формулы двойного аргумента, понижающие степень, а именно

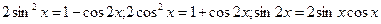
Пример

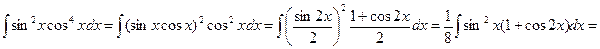
с) Если m<0 и n<0 и сумма их четна, то применяется подстановка t=tgx или t=ctgx. Исходный интеграл сводится к сумме интегралов от степенных функций.

Пример

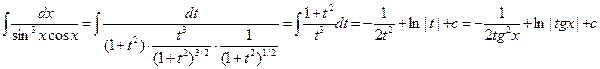
d) Если m<0 и n<0, то единица в числителе представляется как , где 2k=|m+n|-2

Пример

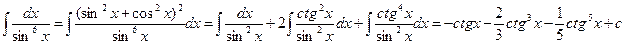e)Если m=0, n – нечетное отрицательное или n=0, m – нечетное отрицательное, то используется универсальная подстановка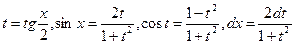

Так как и

Пример

2. Рассмотрим интеграл вида 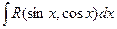. При вычислении такого интеграла возможны различные случаи представления подынтегральной функции:

a) Функции sinx, cosx – только в четных степенях. Тогда можно использовать подстановку . Интеграл упрощается.

Пример

Замечание Такой же подстановкой вычисляется интеграл вида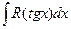

Пример

. Это после разложения на простейшие дроби, вычисления интегралов от них и возврата к старой переменной.

b) Функция R(sinx,cosx) имеет вид 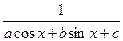. В этом случае применяется универсальная подстановка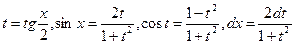

Замечание Использование универсальной подстановки всегда приводит к цели, но в силу своей общности она часто не является наилучшей в смысле краткости и простоты необходимых преобразований.

3.В теории рядов Фурье, важное значение имеют интегралы

. Они вычисляются на основании формул тригонометрии:

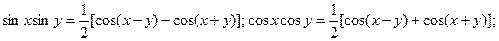
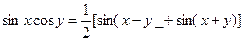
Пример