Магнитные цепи с постоянными магнитными потоками

Магнитной цепью (МЦ) называется совокупность различных ферромагнитных материалов и неферромагнитных частей ЭТУ для создания магнитных полей различной конфигурации и интенсивности.

В зависимости от принципа действия ЭТУ магнитное поле может возбуждаться или постоянным магнитом либо катушкой с током, расположенной в той или иной части магнитной цепи. ЭТУ использующие магнитные цепи очень разнообразны: роторы и статоры электрических машин, магнитопроводы трансформаторов, электромагнитные реле (в них имеется неподвижный и подвижные части магнитопровода); магнитопроводы измерительных устройств и другие.

Алгебраическая сумма токов катушек создающих магнитное поле называется магнитодвижущей силой F (МДС).

,

где число витков в катушке К.

Магнитодвижущую силу можно трактовать как меру сторонних сил создающих магнитное напряжение на концах источника магнитной энергии.

Закон полного тока для магнитных цепей.

Установлено, что алгебраическая сумма произведений напряженности магнитного поля возбуждаемых токами на длину соответствующих однородных участков магнитной цепи постоянной напряженности равна алгебраической сумме всех магнитодвижущих сил.

.

Знак тока в сумме определяется согласно правилу буравчика. Если ток 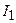создает магнитное направленное в плюс, а ток в минус, то знаки токов их в формуле противоположны.

В интегральной форме запись имеет вид:

.

Схема замещения магнитных цепей и их электрическая аналогия

Из закона полного тока следует аналогия между анализом магнитных и электрических цепей (Табл. 4.1)

Табл. 4.1 Соответвствие электрических и магнитных величин

Электрические величины	Формула	Магнитные величины	Формула
Ток	I	Магнитный поток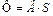
Напряжение		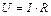Магнитное напряжение
ЭДС		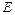МДС
Сопротивление		Магнитное сопротивление

Закон Ома для магнитной цепи :

,

где суммарное сопротивление линейного и нелинейного участков магнитной цепи.

Магнитное напряжение равно произведению магнитного потока на магнитное сопротивление участка цепи.

Аналоги уравнений Кирхгофа для магнитных цепей:

I закон. Алгебраическая сумма магнитных потоков в магнитном узле равна нулю: .

II закон. Алгебраическая сумма магнитных напряжений в замкнутом магнитном контуре равна алгебраической сумме МДС действующих в этом контуре.

.

Из этих законов следует что:

.

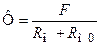Магнитный поток в замкнутой магнитной цепи равен отношению МДС к полному магнитному сопротивлению цепи.

Схему замещения можно представить (как и в электрических цепях) в виде источника магнитной энергии с МДС F и последовательно соединенных с ним магнитных сопротивлений.

Рис. 4.4 – Схема замещения

Основные задачи анализа магнитных цепей

При анализе магнитных цепей решают две задачи:

1) По заданному магнитному потоку и геометрии и магнитным свойствам магнитопровода найти МДС .

2) По заданной МДС и геометрии и магнитным свойствам магнитопровода найти магнитный поток Ф.

Магнитные цепи, как правило, нелинейные!

Пример:На магнитопровод с заданными размерами (рис. 4.5) надета катушка с числом витков 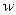. По катушке протекает ток . Запишите закон полного тока.

Рис. 4.5 – Магнитопровод с заданными размерами катушки

Закон полного тока:

.

Запишем закон Ома:

.

Из формулы видно, что если увеличить зазор (и не изменять другие размеры), то так как магнитное сопротивление зазора равно 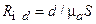, то общее магнитное сопротивление увеличиться. Из закона «Ома»: следует, что магнитный поток Ф в магнитопроводе уменьшиться.