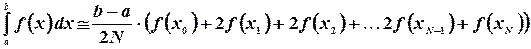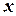Вычисление площадей плоских фигур

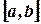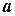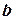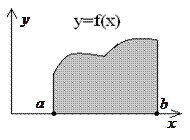
Площадь криволинейной трапеции (явное задание функции). Зададим на отрезке ( и - конечные числа) неотрицательную, непрерывную функцию 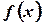, график которой изображен на рисунке.

Произведем разбиение отрезк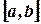а на 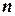- частей точками

Выберем на каждом из полученных частичных отрезков 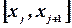( ) по произвольной точке 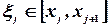. Определим значения функции 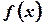в этих точках и составим сумму

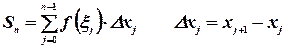
которую называют интегральной суммой и которая, очевидно, равна сумме площадей заштрихованных прямоугольников, как показано на рисунке.

Предел, к которому стремится интегральная сумма, когда называется определенным интегралом от функции 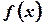на отрезке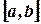

Если функция 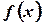отрицательна внутри отрезка 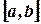, то интеграл по абсолютному значению равен площади, покрываемой графиком, но имеет отрицательное значение (см. рис.).

Пусть теперь 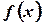меняет знак на интервале 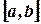, как показано на рисунке.

В этом случае определенный интеграл будет подсчитываться как

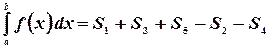
Пример. Найти площадь фигуры, ограниченной линией в пределах интервала 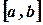, где 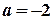, (см. рисунок). Имеем.

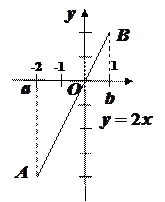
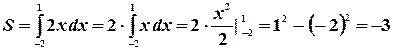
Это число 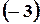равно разности площадей

и

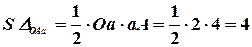
Параметрическое задание функции.

Пусть кривая 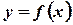, ограничивающая исследуемую фигуру, задана параметрически: 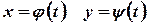. В этом случае дифференциал 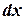будет равен: . И, следовательно, площадь фигуры будет определяться следующим выражением:

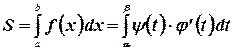
где .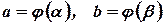

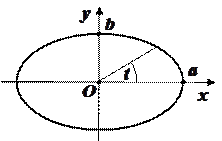Например, надо найти площадь эллипса. Уравнение эллипса в параметрическом виде записывается как

Действительно: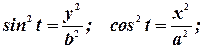

Отсюда

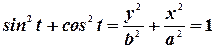
Тогда четвертая часть площади эллипса (в первом квадранте) будет рассчитываться как

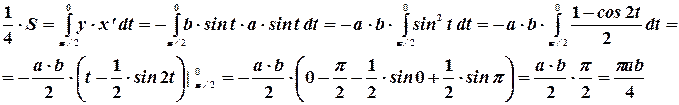
Отсюда площадь эллипса равна .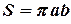

Площадь криволинейного сектора (кривая в полярных координатах) дается формулой

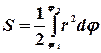
Действительно, согласно рисунку, площадь элементарного сектора представляет собой площадь треугольника, равную половине произведения основания на высоту

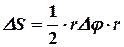
Отсюда вытекает основная формула.

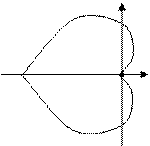
Например. Найти площадь фигуры, ограниченной кривой - Кардиоида

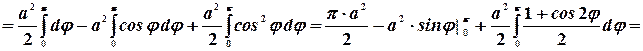
Отсюда площадь кардиоиды равна .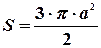

8. Вычисление длины дуги плоской кривой.

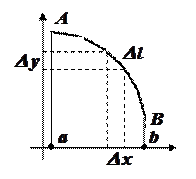Длинна кривой – это предел длины вписанной ломанной, когда длина наибольшего звена стремится к нулю. Если этот предел существует, то кривая называется спрямляемой.

Теорема. Пусть дана непрерывная, дифференцируемая на 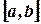функция 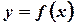. Следовательно, ее производная тоже непрерывна, причем 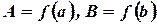. Тогда длина дуги графика функции определяется выражением

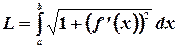
Доказательство. Согласно рисунку, . Отсюда длина элементарной дуги будет равна . Длина всей дуги будет равна

Пример. Найти длину окружности.

Имеем 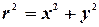, отсюда следует, что . Найдем производную . Следовательно, длина окружности будет равна

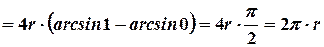
Кривая задана параметрически.

В этом случае . Тогда 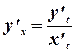. Следовательно

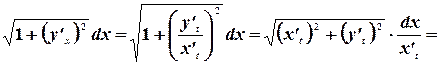
И, соответственно

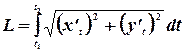
Пример.

Найти длину дуги

Имеем , .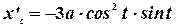

Длина дуги будет равна

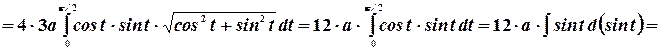
Кривая задана в полярных координатах, что представляет собой частный случай параметрического задания кривой, где параметром выступает угол .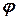

В этом случае: , .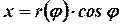

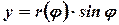Далее , .

Подынтегральное выражение будет равно:

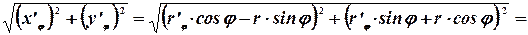
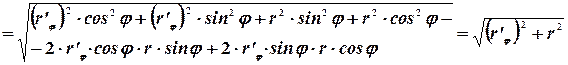
Таким образом, длина дуги в полярных координатах будет определяться выражением

Пример. Вычислить длину кардиоиды .

Имеем . Тогда

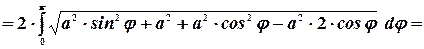
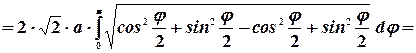
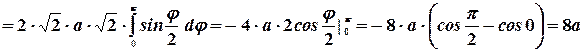
9. Вычисление объём тела по площади поперечного сечения.

Пусть нам дано тело, известные площади поперечного сечения 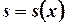которого расположены перпендикулярно оси 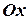, как показано на рисунке.

Тогда элементарный объем этого тела будет равен

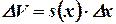
Соответственно полный объем этого тела будет выражаться формулой

Пример. Найти объем конуса, высоты 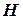и радиуса основания . Согласно рисунку запишем

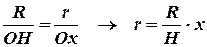
Следовательно, площадь произвольного сечения будет равна

Тогда объем конуса будет равен

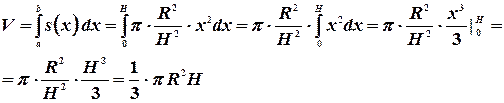
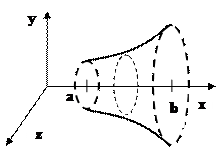10. Вычисление объем тела вращения.

Формула для объема получается из предыдущей

Пример. Найти объем эллипсоида с осями , , .

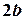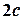Имеем уравнение эллипсоида . Для какой-то произвольной точки 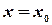запишем

То есть в произвольном сечении мы получили эллипс с полуосями

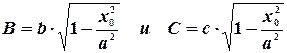
Площадь эллипса равна

Следовательно, объем эллипсоида будет равен

y

y

y

y

11. Приближенное вычисление определенного интеграла

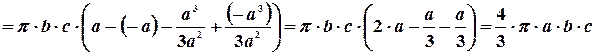
Пусть надо вычислить определенный интеграл от непрерывной на отрезке 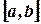функции 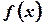и при этом первообразная нам неизвестна.

Простейший способ приближенного вычисления интеграла вытекает из его определения

Эта формула называется квадратурной формулой прямоугольников, поскольку площадь фигуры под графиком функции мы разбиваем на элементарные прямоугольники.

Можно площадь фигуры разбивать не на прямоугольники, а на трапеции, образованные секущими. В этом случае приближенное значение интеграла будет рассчитываться как