Коэффициент учета второстепенных работ – коэффициент фиктивности - .Учет теплоотдачи и прорыва пороховых газов

Рассмотрим виды работ совершаемые пороховыми газами :

1. L₁ - работа поступательного движение снаряда – главная работа .

(9.32)

2. L₂- работа, затрачиваемая на вращение снаряда (9.33) ,

где

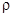-радиус инерции снаряда , определяемый по формуле , где I- момент инерции относительно оси вращения

r=d/2- радиус сечения снаряда

-угол нарезки

- крутизна нарезов

h- шаг нарезки

обычно 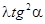от 0,25% до 2,5%

К₂=0,0025-0,025

L₃- работа на преодоление трения между пояском снаряда и внутренней поверхности канала ствола , а также на преодоление трением между центрующими утолщениями снаряда и полями нарезов (9.34) ,где 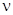₁ -коэффициент трения

4. L₄- работа затрачиваемая на перемещение газов самого заряда и несгоревшего пороха . В предположении о постоянстве плотности 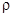газопороховой смеси по всему за снарядному пространству .т.е. плотность 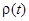зависит только от времени и не зависит от координаты сечения и в самом сечении , энергия , затрачиваемая на перемещение заряда , будет выражаться зависимостью :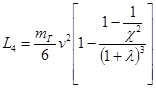 (9.35) , где , , 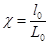где l₀- приведенная длина каморы =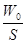

L₀- действительная длина каморы

l- путь пройденный снарядом

Работа L₄ вычисленная по формуле (9.35) будет больше действительной работы , т.к. плотность газопороховой смеси уменьшается в направлении к снаряду , что доказывают газодинамические расчеты .

5. Работа затрачиваемая на перемещение откатных частей.

(9.36)

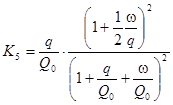, где 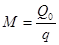-масса откатных частей ; Q₀ –вес откатных частей .

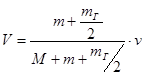(9.37) ,где V –скорость откатных частей

m_г= 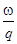-масса заряда, т.к. и , то

L₆ –работа , расходуемая на врезание ведущего пояска в нарезы . Как правило не учитывается и может быть учтено косвенно в момент вылета снаряда из ствола .

L₇ –работа, расходуемая на преодоление снарядом сопротивления воздуха , находящегося в канале орудия . Этой работой при малых скоростях пренебрегают . Однако при скоростях 2,5-3 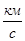противодавление уже составляет 150-300 и учет противодавления необходим .

- тепловая энергия , расходуемая во время выстрела на нагрев стенок ствола , гильзы и снаряда – потеря на теплоотдачу . Учитывается путем уменьшения силы пороха ,-f.

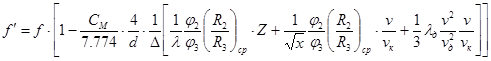(9.38)

в момент времени t при t=0 ,

при t=t_д

,где

; ; ; ; ;

; ; ; ; ; ;

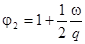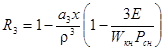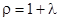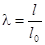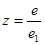l –путь снаряда

-скорость снаряда

С_м% -определяется по кривой С% от t_к при 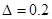кг/дм²

d –калибр снаряда

l_км –длина каморы

W_кн –объём канала ,включая камору

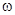- вес заряда

q –вес снаряда

Р_сн – давление на снаряд

Таким образом , сила пороха по мере движения снаряда по каналу за счет теплоотдачи убывает ; она зависит от :

1) калибра-d

2) плотности заряжания -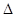

3) коэффициента уширения каморы -

4) относительного пути снаряда -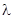

5) отношения скоростей

При выводе использовалось предположение , сделанное Мюреуром :

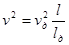и соотношение , сделанное профессором Вентцелем.

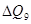- энергия , теряемая газами , прорывающимися по зазорам между пояском снаряда и стенками канала орудия.

(9.39)

где ; - относительная часть прорвавшихся газов

Если расход газа невелик , то , или с учетом теплоотдачи .

Значение ,где a=1.09-1.03 и b= - для цилиндрических каналов и и - для конических каналов.

9.5 Анализ изменения давления пороховых газов в канале ствола от условий заряжания .

Имея формулу для давления из основного уравнения пиродинамики (9.19)

,

исследуем ,как будет меняться давление в зависимости от пути и времени . Для этого найдем производные :

(9.40)

, или , , ,

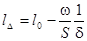
Как видно из выражения (9.40) нарастание давления зависит от многих факторов .

В момент формообразования Р=Р₀

, нарастание давления зависит от Р₀,f и ,и обратно пропорционально , при Р₀=0 (для миномета ) ,тангенс угла наклона будет равен 0 . И далее тангенс угла наклона возрастает до точки перегиба и далее тангенс угла наклона убывает до 0 и далее становится отрицательным за счет значения .

На рис. ….. фиг. 91 показан характер этих кривых .При получим соотношение , в момент ….. горения при ,

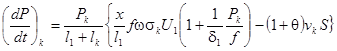
При переходе ко второму периоду выражение для давления имеет вид , , ,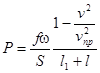

Характер нарастания давления в функции от пути –l выразится общей формулой (9.41)

Вначале движения ,когда тангенс угла наклона равен ∞ ,т.е. кривая Р(l) будет иметь касательную совпадающую с осью ординат рис.(фиг.92)

9.6 Влияние формы и размеров пороха на кривые давления газов и скорости снаряда.

Анализ формул (9.40) и (9.41) показывает ,что характер нарастания давления как во времени так и функции от пути снаряда зависит , главным образом от при данной "силе" и природе пороха зависит от

Для простоты , рассмотрим случай когда зёрна имеют одинаковую толщину , но разную форму . Взяв для пяти дегрессивных форм общие формулы и примерные числовые данные имеем таблицу :

	форма зерна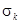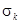
	трубка				1,003	0,0994	0,997
	лента				1,06	0,89	0,943
	пластинка				1,20	0,675	0,810
	брусок				~2,0
	куб

Нанеся на график изменение в зависимости от Z получим диаграмму изображенную на рис(фиг.93). На рис(фиг.94) приведены расчеты давлений газов при и в функцию от пути . Диаграмма показывает ,что лента дает нормальное давление и дульную скорость

.Брусок –4 , имея большую начальную оголенность дает давление и . Куб –5 в следствии втрое большей оголенности имеет давление и 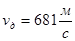. Если бы поставить задачу : сравнить дульные скорости при одинаковых Р_m ,то ленточный порох показал наилучшие результаты .

Теперь рассмотрим влияние толщины свода при одинаковой форме зерна . Результаты расчетов сведены в таблицу :

2
1,5	1,414	1,256
2,0	1,06	0,943
2,5	0,848	0,744

Влияние толщины пороха на кривые давления показаны на рис…(фиг.96)

10. Решение основной задачи внутренней баллистики (ОЗВБ).

Установление закономерностей , связывающих разнообразные условия заряжания с зависящими от них величин , называемыми баллистическими элементами выстрела составляет общую задачу внутренней баллистики .

К условиям заряжания относятся : размеры каморы и канала ствола , его вес , устройство нарезка в канале , вес и устройство снаряда ,давление форсирования , зависящее от устройства пояска снаряда и нарезки канала , вес заряда , марка пороха , физико-химические и баллистические пороха , характеристики расширения газов .

К баллистическим элементам выстрела относятся : изменяющееся во времени путь снаряда –l, скорость снаряда , давление пороховых газов –Р, их температура – Т , а также количество газов , образовавшиеся к данному моменту ; а также относительная толщина горящего свода –Z.

При решении указанной выше ОЗВБ можно выделить две важнейших основных задач пиродинамики и ряд частных задач .

Первая основная задача пиродинамики состоит в определении расчетом изменения газов и скорости снаряда в канале ствола в функции от пути снаряда и от времени при заданных условиях заряжания . При этом наряду с кривыми Р(l),υ(l) или P(t),υ(t) и l(t) определяются две важнейшие баллистические характеристики орудия – наибольшее давление газов –Р_m в канале ствола и дульная скорость снаряда - ,т.е. скорость снарыда при вылете его из канала ствола . Эту задачу называют прямой задачей пиродинамики . При заданных условиях заряжания она иееет единственное решение. Изменяя условия заряжания можно провести анализ этих условий на изменение кривых давления газов и скорости снаряда ,т.е. решить ряд частных задач . Точность решения этой задачи зависит от выбранной математической модели выстрела и методов решения . Вторая основная задача пиродинамики – задача баллистического проектирования орудия состоит в определении конструктивных данных канала ствола и условий заряжания , при которых снаряд данного калибра-d и веса-q , получает при вылете определенную дульную скорость - .Эта скорость задается на основе тактико-технических требований ,предъявляемых к проектируемому орудию . При решении её обычно , задаются наибольшим давлением газов –Р_m. Решение этой задачи многовариантно от целесообразности и рациональности выбранного варианта баллистического решения в значительной степени зависит дальнейшее проектирование всей артиллерийской системы в целом и боеприпасов к ней . По выбранным условиям заряжания производится расчет кривых давления и скорости . Полученная кривая Р(t) или P(l) используется конструкторами для расчета прочности стенок орудия и снаряда , лафета ,дистанционных трубок , взрывателей . Вместе с этим даются требуемая толщина и форма пороха , который должен быть изготовлен на заводе .

Здесь возникают специальные частные задачи о нахождении наивыгоднейших решений , от орудий наибольшего могущества , об орудии наименьшей длины или объёма , о наивыгоднейшем заряде и наивыгоднейших условий заряжания .

Методы решения решения задач пиродинамики можно разделить на аналитические , численные , эмпирические и табличные.

В настоящее время , в связи с появлением персональных быстродействующих ЭВМ , все большее значение приобретают численные методы , в которых постановка задачи ставится более шире , чем в других методах решения , но в численных методах используется целый ряд допущений.

Основные допущения при решении ОЗВБ:

1. Горение пороха подчиняется геометрическому закону горения или физическому закону горения.

2. Порох горит при средних давлениях p , воспламенение мгновенное.

3. Состав продуктов горения не меняется (f и 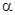- постоянные).

4. Скорость горения пороха пропорциональна давлению .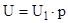

5. Учитываемые второстепенные работы пропорциональны главной работе поступательного движения снаряда и учитываются при помощи коэффициента .

6. Движение снаряда начинается , когда в каморе в результате сгорания части заряда разовьется давление форсирования –p₀ , постепенность врезания в n не учитывается.

7. Работа врезания пояска отдельно не учитывается.

8. Растяжением стенок ствола при выстреле , прорывом газов через зазоры между ведущим пояском и стенками канала ствола и сопротивлением воздуха в канале ствола пренебрегаем.

9. Охлаждение газов в результате теплоотдачи стенкам ствола непосредственно не учитывается и может принято в расчет косвенно , снижением f и увеличением .

10. Движение снаряда рассматривается до момента прохождения его дна через дульный срез.

11. Величину принимаем равной среднему значению для всего периода выстрела.

12. Плотность газопороховой смеси зависит только от времени и не зависит от координаты.

Таким образом уравнения классической внутренней баллистики для усредненных значений давлений p, температуры T и относительного количества сгоревшего заряда 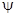, при этом осреднение T и 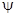получается как следствие осреднения давления . Иначе говоря , в классическом методе внутренней баллистики волновые процессы течения газа не учитываются , и применяется "термодинамический" закон расширения газов .

Этот классический метод расширения дает хорошие результаты для относительно тяжелых снарядов , когда , т.е. когда в области действия первой волны разряжения , снаряд не набирает значительной скорости и первая волна разряжения от дна каморы догоняет снаряд вблизи начала координат , и учет первой волны разряжения будет несущественным , т.к. далее устанавливается "термодинамический" режим расширения пороховых газов .

Для нахождения элементов выстрела в классическом методе О.З.В.Б. имеем следующие зависимости :

1) - основное уравнение пиродинамики , уравнение Резаля .

2) или - закон горения пороха .

3) 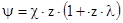- двухчленный закон газообразования .

4) - закон движения снаряда .

5) - кинематическая связь между скоростью и путем .

Совокупность этих 5-ти уравнений позволяет найти 5-ть неизвестных p,z,υ,l, 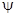как функции времени.

10.1 Система уравнений ОЗВБ для пороха простой дигрессивной формы.

Для вычисления элементов выстрела по имеющейся специальной программе, по которой решается система обыкновенных дифференциальных уравнений 1-го порядка на ПЭВМ (macad) приведем наши уравнения к нормализованному виду (система 10,1)

(10,1)

где l = ; .

Система уравнений ( 10,1 ) решается при следующих начальных данных :

при t = 0 , z =0 , 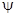= 0 , p = p_в , υ = 0 , l = 0 , конец расчета l = l_д .

Точность и правильность расчета проверяются по аналитическим зависимостям в момент p = p₀ :

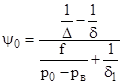
При горении пороха :

где p_m , z_m , V_m – значения давления , скорости и относительной толщины в момент максимального давления .

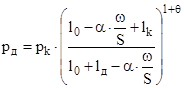
где υ_пр =

Правильность решения проверяется при различных условиях заряжания в постоянных переменных Н.Ф. Дроздова :

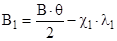
10.2 Системы уравнений для многоканального пороха прогрессивной формы .

При решении ОЗВБ для многоканального пороха воспользуемся двухчленными формулами для 1-й фазы горения ( до распада зерна ) и 2-й фазы горения ( после распада зерна ) . Для 1-й фазы горения характеристики

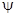и найдутся из условия , что при z = 1 и при z = 0,5 значения будут совпадать как по трехчленной , так и по двухчленной формулам :

при z=0,5

при z=1

откуда имеем

,

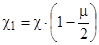Для второй фазы горения имеем

характеристики и 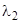найдутся из условия , что при z=z_k и при

z=z_k поверхность горения должна обратиться в ноль . Откуда получим :

Решая находим эти уравнения:

Подсчитав χ и λ по этим формулам для 7-ми канального стандартного пороха имеем :

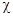=0,712 ; 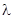=0,225 ; = - 0,0237 ; =0,855 ; =1,375 ; ; =0,1873 ;

ошибка =0,004 .

Принимая для 7-ми канального пороха наружный радиус вписанного круга в наружную призмочку 0,532е₁ получим е_к=е₁+0,532е₁=1,532е₁

; =0,855 ; 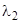= - 0,94 ;

Для зерна Уолша с 7-ю каналами ; =0,95 ; 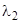= - 2,16 ;

=1,37 ; ; =0,218 .

Исходя из 2-х фаз горения : прогрессивного в первой фазе и дегрессивного во второй фазе система уравнений ( 10,2 ) будет иметь следующий вид

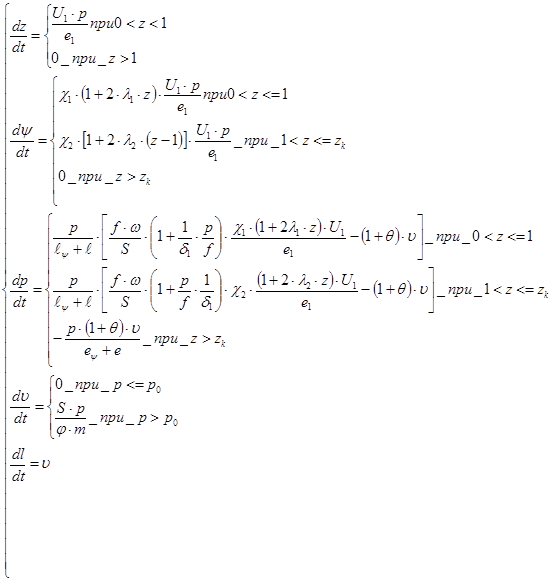(10.2)

где ;

Система ( 10,2 ) решается при следующих начальных данных : при t = 0 , z=0, 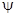=0 , p = p_в , l = 0 , υ= 0 . Расчет заканчивается при l = l_д . Точность и правильность расчета проверяется как при расчете системы ( 10,1 ) .

10.3 Системы уравнений для комбинированного заряда из дегрессивных порохов простой формы .

Пусть комбинированный заряд состоит из n порохов дегрессивной простой формы . Характеристики i-того пороха обозначим с индексом i , так что

, где i =1...n .

Весовую долю каждого пороха обозначим через , тогда по правилу смешения можно найти фиктивный эквивалентный порох , имеющий такие же характеристики как комбинираванный пороховой заряд :

; ; ; ;

Расставив пороха по импульсу в конце горения , пороха по возрастающему значению J₁<J_i<J_n и воспользовавшись системой уравнений ( 10,1 ) окончательно получим

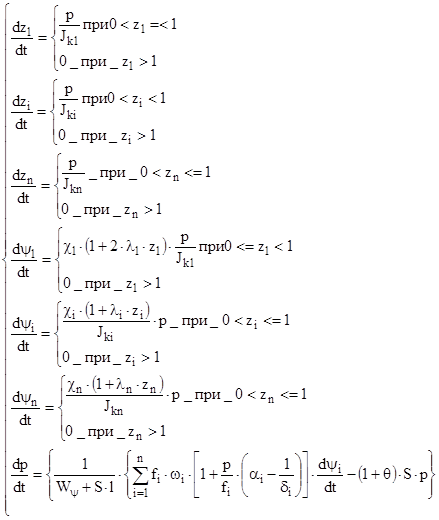( 10,3 )

где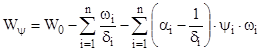

Точность решения системы уравнений проверяется по аналитическим зависимостям , по которым проверяется точность системы ( 10,1 ) . При этом необходимо брать характеристики эквивалентного фиктивного пороха f , J_k ,

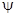, Г , , , 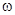формулы которых приведены выше . Значения 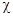и 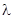такого пороха определяются по формулам ( 10,4 )

( 10,4 )

Уравнение газообразования примет вид :

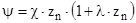( 10,5 )

10.4 Системы уравнений для комбинированного заряда , состоящего из 7-ми канального и трубчатого порохов .

В артиллерийских орудиях среднего и крупного калибра пороховой заряд состоит из центрального пучка , содержащего трубчатый порох , заданного по чертежу веса , вокруг которого размещается в ... картузе переменный заряд 7-ми канального пороха того же состава .

При приемке партии варьируется вес только зерненного пороха . Ниже приведена система уравнений для такого комбинированного заряда .

Пусть трубчаты порох имеет индекс – Т . 7-ми канальный имеет обозначения такие же как в системе ( 10,2 ) . ОЗВБ для такого заряда решается по системе уравнений ( 10,6 ) :

(10,6 )

Фиктивный порох эквивалентный комбинированному заряду имеет следующие баллистические характеристики :

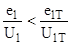1) при где

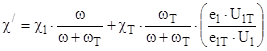
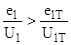2) или при где

Точность решения системы проверяется по аналитическим зависимостям , представленным выше , которые справедливы в 1-м случае – до распада зерна 7-ми канального пороха , во втором случае – до конца горения трубчатого пороха , который наступает раньше распада зерна .

10.5 Исходная система уравнений внутренней баллистики для миномётов, орудий и ракет.

Рассмотрим систему уравнений , базирующуюся на единой теплофизической модели для различных по схемам действия и конструктивному оформлению орудий ( классическое артиллерийское орудие , динамо реактивные системы , РДТТ и другие ) . Впервые , это важное с методической и практической точек зрения , придложение было высказано и реализовано профессором Б.В. Орловым .

За основу исследований при выводе системы уравнений принимаем частично уравновешенное орудие рис... , для которого справедливо соотношение :

( 2,13 )

где n – коэффициент уравновешенности ; S – площадь поперечного сечения канала ствола с учетом нарезов ; p – баллистическое давление ( среднее давление газов в за снарядном пространстве в данный момент времени ) ; G_p1- расход газов через сопловой блок орудия , имеющий размерность "кг/с" ;

J_r – удельный импульс , развиваемый пороховыми газами при истечении из сопла .

Величина коэффициента уравновешенности "n" ограничена пределами 0<=n<=1 . Для классического артиллерийского орудия n = 0 , для безоткатного n =1 .

Будем полагать так же , что имеет место прорыв пороховых газов через ведущее устройство снаряда , количественно характеризующееся расходом

G_p2 , а так же имеется теплоотдача стенкам канала ствола , и стенка ствола расширяется упруго при выстреле .

Исходную систему уравнений запишем при следующих допущениях :

1. Горение пороха происходит параллельными слоями , т.е. справедливо уравнение газоприхода и относительную поверхность горения : где

- характеристики формы пороха ; z = - относительная толщина сгоревшего пороха ; e₁ – половина толщины порохового зерна ; e – толщина слоя сгоревшего пороха ; - сгоревшая часть порохового заряда ; 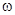- вес заряда ; S_гор – горящая поверхность заряда ; S_горо – начальная поверхность заряда .

2. Давление p , температура Т и плотность газопороховой смеси 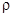в заснарядном пространстве для каждого момента времени t равны их среднему по объему значениям ( гипотеза квазистационарного процесса ) .

p , T и 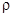связаны уравнением состояния :

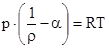
где R – газовая постоянная ; 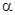- коволюм газа .

3. Состав продуктов сгорания не меняется во время выстрела , а удельные теплоемкости C_p , C равны их средним значениям для всего диапазона изменения температур .

и = const .

4. Воспламенение порохового заряда происходит мгновенно .

5. Отсутствует выброс несгоревших частиц пороха .

6. Противодавлением воздуха в канале ствола пренебрегаем .

При выводе системы уравнений используем основные законы термодинамики :

закон сохранения энергии – первого закона термодинамики запишем в виде :

здесь 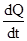- скорость изменения тепла в газе , вес которого , к рассматриваемому моменту времени составит , вследствие его взаимодействия с окружающей средой .

- скорость изменения внутренней энергии газа , где U= (2,15)

- мощность , развиваемая газом при его расширении или при сжатии .

Применительно к периоду движения снаряда при горящем заряде :

( 2,16 )

Здесь - скорость подвода тепла вследствие сгорания порохового зерна , где Е = 4270 - механический эквивалент тепла;

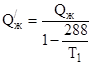
- калорийность пороха при воде жидкой , т.к. .

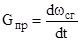- приход продуктов сгорания .

- скорость оттока тепла из каморы орудия в атмосферу вследствие истечения газов через сопло ( G_p1 ) и в зазоры между ведущими устройствами снаряда и стенками канала ствола ( G_p2 ) .

- энтальпия одного кг газа .

- скорость изменения тепла в следствие теплоотдачи между стенками ствола и газами ( символ показывает , что не является полным дифференциалом ) .

Скорость отвода тепла из-за снарядного пространства в стенке канала ствола:

( 2,17 )

где - коэффициент теплоотдачи от газа к стенкам ; Т_сг – температура внутренней поверхности ствола ; F – поверхность , омываемая газами .

Точно уравнение ( 2,17 ) решается совместно с уравнением теплопроводности материала стенки при соответствующих краевых условиях. Величина в общем случае выражается уравнением :

( 2,18 )

Здесь W – свободный объем за снарядного пространства ;

- мощность , создаваемая газом , вследствие сгорания заряда с учетом истечения части газа из за снарядного пространства , где 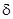- удельный вес пороха ;

- мощность , затрачиваемая на упругие деформации стенок , гильзы и ствола , где - "упругое" приращение за снарядного объема . Обычно этой мощностью пренебрегают , хотя в пушках высоких давлений она может являться ощутимой ( ППН,ЛГУ ) .

( 2,19 )

Мощность расходуемая на поступательное движение снаряда с фиктивным весом , где q – вес снаряда , - коэффициент фиктивности или коэффициент , учитывающий поступательное движение снаряда , его вращение , преодоление вредных сопротивлений , откат откатных частей , выталкивание столбов воздуха и , наконец , работу на перемещение газопороховой смеси .

Обычно в расчетах принимается постоянным :

( 2,20 )

где к зависит от калибра и начальной скорости снаряда и типа снаряда .

С уменьшением калибра снаряда величина "к" – возрастает и уменьшается с ростом начальной скорости . Для снаряда с ведущим пояском "к" = 1,02-1,05.

Для пуль , имеющих калибр меньше 14,5 мм и не имеющих ведущего пояска

"к"=1,2-1,3 .

С учетом выражений ( 2,15 ) , ( 2,16 ) , ( 2,18 ) уравнение сохранения энергии применительно к рассматриваемой схеме ( рис... ) приводится к виду :

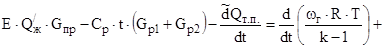
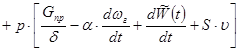( 2,21 )

Соотношение ( 2,21 ) так же называют основным уравнением внутренней баллистики . Уравнение сохранения вещества может быть записано в виде

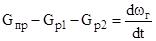( 2,22 )

Приход газов в следствии сгорания пороха 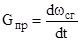определяется по формуле

( 2,23 )

Значения G_p2 , G_p1 зависят от значений полной температуры T₀₀ и полного давления газов p₀₀ в за снарядном пространстве , а так же площадей критических сечений сопла и зазор F_з . При расчете G_p2 следует дополнительно учитывать скорости снаряда и формы зазоров во времени

- коэффициент расхода , который учитывает особенности истечения пороховых газов через появившийся зазор и определяется экспериментально член - скорость изменения количества газов в за снарядном пространстве . Уравнение движения снаряда :

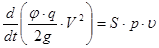или ( 2,25 )

Уравнение состояния :

где

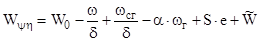
где

Для решения основной задачи внутренней баллистики должны быть известны законы скорости горения пороха U=U_p и изменения поверхности порохового зерна в функции толщины горения свода е ( или z ) . Таким образом параметры состояния газа , а так же скорость и путь снаряда до момента вылета его из ствола могут быть найдены из следующей системы уравнений :

(2,26)

Накладывая определенные ограничения , с помощью полученной системы уравнений (2.26) можно описать процессы выстрела в следующих системах:

1. Безоткатные орудия (n=1).

2. Миномет (n=0 , G_p1=0).

3. Классическое орудие (n=0 , G_p1=0 , G_p2=0).

4. Ракетный двигатель (G_p2=0 , υ=0).

5. Бомба постоянного объема ( G_p1=0 , G_p2=0 , υ=0).

Если параметры состояния газов определяются после окончательного горения заряда в системе (2.26) необходимо положить S_гор=0 и U=0.

После вылета снаряда из канала ствола расчет продолжается при S_гор=0 и U=0 и F_з=S и из системы (2.26) исключается уравнение движения снаряда.

Внутренняя баллистика классического орудия.

Для закона сохранения энергии , когда G_p1=0 , G_p2=0 в момент горения пороха будем иметь:

(2.27).

В предварительном периоде горения пороха идет при υ=0 и l=0 до момента p=p₀ и 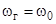, где p₀- давление форсирования снаряда;

количество газа , образовавшегося в момент t=t₀ – форсирования снаряда. Интегрируя уравнение (2.27) получим:

( 2,28 )

На 2-м периоде – периоде расширения пороховых газов ( S_гор = 0 , U = 0 ,

) , уравнение сохранения энергии примет следующий вид :

Для предварительного периода ( υ = 0 ) получим

Для приближенного учета теплоотдачи воспользуемся допущением , согласно которому процесс теплоотдачи можно считать квазистационарным,

с коэффициентом теплоотдачи – линейно зависящим от удалённого веса газа в за снарядном пространстве

( 2,29 )

где - постоянный коэффициент теплоотдачи . Т.к. 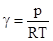, то

=

Введем обозначение , тогда

= ( 2,30 )

Значение находятся из экспериментов . Для автоматических пушек допустимо принимать 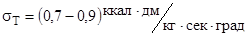, . С учетом этого допущения система ( 2,26 ) примет вид :

( 2,31 )

где J_k =

Учитывая , что

где f – сила пороха , - доля твердых остатков в продуктах сгорания ( для дымных порохов = 0,5 ; для бездымных порохов = 0 ).

( 2,32 )

где

т.к. и

то получим

( 2,33 )

Подставляя выражение ( 2,33 ) в первое уравнение системы ( 2,32 ) окончательно получим :

( 2,34 )

где F = S₀ +

;

Если пренебречь растяжением стенок ствола ( ) окончательно получим систему уравнений с учетом теплоотдач :

( 2,35 )

где ;

.

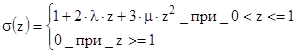
Рассмотрим учет теплоотдачи при выстреле предложенный Мюрауром для бомбы , принимая во внимание постепенное возрастание охлаждающей поверхности стенки :

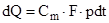( 2,36 )

где C_m – экспериментально найденный коэффициент в бомбе при сжигании дымного пороха по времени сгорания его при 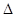= 0,2 кг/дм³ .

Имеется кривая C_m=C_m(t_k) или таблица , по которой C_m можно определить .

С другой стороны имеем :

( 2,37 )

Согласно формуле профессора Мамонтова М.А.

( 2,38 )

где - коэффициент теплопередачи для газов при U = 0 .

- плотность пороховых газов

U – скорость течения газов у стенки

n – показатель степени : n = 0,5-1

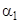- скоростной коэффициент , определяемый из опытов .

Сравнивая ( 2,36 ) и ( 2,37 ) получим :

( 2,39 )

Коэффициент C_m^/ учитывает скорость течения пороховых газов в орудии .

В мfнометрической бомбе U=0 и C_m^/ = C_m ,тогда

( 2,41 )

где - потеря температуры пороховых газов за счет теплоотдачи ;

T₁ – температура горения пороха ;

7,774 – переходной коэффициент от бомбы Мюраура к нашим условиям .

Поверхность теплоотдачи F = ( 2,42 )

где F₀ = - поверхность каморы орудия ;

l_кам – длина каморы ;

Д – диаметр каморы ;

d – диаметр канала ствола ;

l – пройденный путь снарядом в канале ствола ;

- коэффициент , учитывающий поверхность граней нарезов ;

t_n – глубина нарезов ;

n – число нарезов .

Объем каморы

где

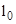- приведенная длина каморы ;

S- площадь сечения ствола ;

- уширение каморы .

Учитывая , что сила пороха f = RT₁ , то введя значение f₁ = (2,43)

мы придем к системе уравнений имеющей вид ( 11,1 ) принимает вид системы ( 2,44 )

( 2,44 )

где

;

W₀ =

; ;

Начальные условия :

при t = 0 , p = p_в , V = 0 , l = 0 , 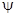= 0 , z = 0 .

Расчет ведется до l = l_д . Шаг интегрирования не более

и уточняется в процессе расчета .

Входными данными являются :

Параметры ствола – Д , l_кам , d , t_n , a , n , l_д .

Параметры снаряда – q , p₀ .

Параметры порохового заряда - .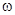

Марка пороха : 2е₁ , или J_к , .

Коэффициент фиктивности или k :

10.6 Баллистическое проектирование артиллерийских стволов .

Задача обычно расчленяется на две части :

1. Устанавливается калибр орудия , тип снаряда и его начальная скорость , обеспечивающая решение поставленной боевой задачи .

2. Определяются размеры канала ствола и характеристики заряда .