Упругий центральный удар»

ИЗУЧЕНИЕ КИНЕМАТИКИ ДВИЖЕНИЯ ТЕЛА, БРОШЕННОГО

ПОД УГЛОМ К ГОРИЗОНТУ».

Цель работы: изучение способов описания движения материальной точки на примере тела, брошенного под углом к горизонту.

Вопросы для допуска к работе:

1. На какие простейшие виды движения удобно разложить движение тела, бро­шенного под углом к горизонту?

2. С каким ускорением происходит это движение?

3. Как найти уравнение траектории движения тела, если известны уравнения его движения? Что понимают под термином «траектория движения»?

4. Иметь протокол выполнения лабораторной работы и знать ход выполнения работы.

Краткая теория:

Движение тела, брошенного под углом к горизонту, является примером криволи­нейного движения. При действии сил, зависящих от времени, координат, и скорости решение задачи является достаточно сложным. Это решение упрощается для случая действия постоянной силы. В частности, если дальность и высота полета тела малы по сравнению с радиусом Земли, такой постоянной силой является сила тяжести. Причем это постоянство относится как к величине, так и к направлению действия силы тяже­сти.

Найдем закон движения тела под действием силы тяжести, когда вектор началь­ной скорости направлен под углом к горизонту. Свяжем систему отсчета с Землей, и будем считать ее инерциальной. Силами сопротивления воздуха пренебрегаем. Систе­му координат выбираем так, чтобы ось OY была направлена вертикально вверх, а век­тор скорости лежит в плоскости XOY (см. рис. 1).

Уравнение движения тела при этих условиях имеет вид:

mg = ma

Запишем это уравнение в проекции на оси X и Y:

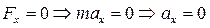
Вывод: движение вдоль оси X равномерное.

Вывод: движение вдоль оси Y равноускоренное.

Теперь нетрудно найти и закон движения тела, брошенного под углом к горизон­ту:

Ось X:

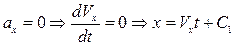, при t = 0, C₁= x₀

Ось Y:

, при t = 0, C₂=V_oy

Найдем уравнение, по которому можно найти координату «Y».

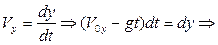
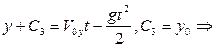
Итак, найдены уравнения, описывающие движение тела брошенного под углом к

горизонту:

Эти уравнения полностью описывают движение тела. Значения Y_ox и Y_oy найдем, вос­пользовавшись рис. 1:

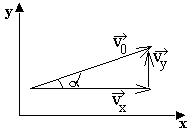Рис. 1

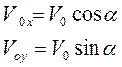
С учетом этого уравнения движения можно записать следующим образом:

Это параметрические уравнения движения. Они позволяют найти уравнение траекто­рии y=y(x). Для этого необходимо из первого уравнения выразить время и подставить его во второе уравнение. Самостоятельно вывести уравнение траектории и сделать вы­вод о виде траектории движения тела, брошенного под углом к горизонту.

Исследование уравнения траектории и параметрических уравнений движения позволяет:

1. Определить горизонтальную дальность полета при заданном угле вылета тела.

2. Найти значение угла, при котором горизонтальная дальность полета будет максимальна, при заданных начальных условиях.

3. Максимальную высоту подъема тела.

4. Общее время полета и момент времени, когда будет достигнута максимальная высота подъема.

5. Определить значение угла, под которым необходимо произвести выстрел, чтобы попасть в точку с заданными координатами.

Исследование произвести самостоятельно при подготовке к выполнению лабораторной работы дома.

Описание лабораторной установки:

При выполнении данной работы используется щит, укрепленный вертикально. На поверхности щита через 5 см пересекаются линии координатной сетки. Точки пересечения имеют сквозные отверстия, используя которые укрепляют ударный датчик и баллистический пистолет. На корпусе баллистического пистолета укреплен угломер, служащий для отсчета угла наклона к горизонту.

Список заданий:

Задание 1: Экспериментально определить скорость вылета шарика из баллистического пистолета.

Метод определения скорости студент может выбрать самостоятельно, восполь­зовавшись уравнением траектории или законом сохранения механической энергии. Для более точного определения значения скорости вылета измерения произвести не менее 10 раз и оценить ошибку в определении значения скорости.

Задание 2: Используя уравнение траектории, начальные условия и значение скорости вылета шарика, а также угол (задается преподавателем) рассчитать траекторию полета шарика. Результаты вычислений представить в виде таблицы:

									…
X
Y

Расчет производить до первого отрицательного значения «Y». Значения координаты «X» изменять через 5 см. Первые значения координат равны начальным координатам. Число столбцов определить исходя "из максимальной дальности полета, которую рас­считать по выведенной при подготовке к работе формуле.

Задание 3: Определить, под каким углом необходимо произвести выстрел, чтобы попасть в точку, координаты которой заданы.

Задание 4: Определить угол, под которым нужно произвести выстрел при данных значениях скорости и начальных координатах, чтобы дальность полета была мак­симальна.

Задание 5: Определить, под каким углом необходимо произвести выстрел, чтобы попасть в точку X<X_max.

Задание 6: Для точки, указанной преподавателем, найти значения радиуса кривизны траектории, нормального и тангенциального ускорения.

ЛАБОРАТОРНАЯ РАБОТА № 4

УПРУГИЙ ЦЕНТРАЛЬНЫЙ УДАР».

Цель работы: экспериментальное изучение закономерностей при центральном упругом ударе.

Вопросы для допуска к работе:

I. Уметь отвечать на следующие вопросы:

1. Понятие механического удара. Явления, сопровож­дающие механический удар. Классификация механи­ческого удара.

2. II закон Ньютона в импульсной форме.

3. Законы сохранения импульса и механической энергии. Границы их применимости.

4. Основные понятия, используемые в теории удара: ударный импульс, средняя сила удара, время взаимо­действия, коэффициент восстановления.

5. Как найти среднюю силу, с которой взаимодействуют шары при ударе?

6. Как в данной работе определяется время взаимодейст­вия шаров?

II. Иметь в протоколе:

1. Краткий конспект ответов на вопросы.

2. Расчетные формулы для определения углов отклоне­ния после взаимодействия, времени взаимодействия шаров, средней силы взаимодействия шаров, коэффи­циента восстановления.

3. Формулы для расчета погрешности.

Р.S. В расчетные формулы должны входить величины, которые определяются экспериментально или могут быть взяты из справочника.

Краткая теория вопроса

В механике под ударом понимают кратковременное взаимодей­ствие двух или нескольких тел, возникающее в результате их сопри­косновения и приводящее к значительному изменению состояния движения. При ударе в течение кратковременного соприкосновения тел происходит их деформация, в результате чего кинетическая энергия ударяющего тела переходит в энергию упругой деформации. При этом возникают упругие силы, возрастающие с увеличением деформации, направленные противоположно относительным скоро­стям соударяющихся тел. Возникающие в результате действия упругих сил ускорения уменьшают скорости тел до тех пор, пока они не станут одинаковыми, или, что то же, пока относительная скорость тел не станет равной нулю.

С момента, когда относительная скорость стала равной нулю, начинается частичное или полное восстановление деформации. Си­лы, продолжая действовать в прежнем направлении, сообщают те­перь взаимодействующим телам положительные ускорения, а, следо­вательно, скорости взаимодействующих тел возрастают по абсолют­ной величине, направление же их меняется на противоположное.

Если в результате удара суммарная механическая энергия не переходит в другие формы энергии, то такой удар называют идеаль­но упругим. Идеальному удару соответствует полное восстановле­ние формы соударяющихся тел.

Если направление движения соударяющихся тел в момент их соприкосновения совпадает с прямой, соединяющей центры масс тел, то такой удар называют центральным.

Явление удара протекает обычно тысячные, и даже миллионные доли секунды. Время, в течение которого взаимодействуют тела при ударе, называется временем соударения.Оно зависит от упругих свойств материала, из которого изготовлены взаимодействующие тела, их относительной скорости в момент начала удара и от их мас­сы.

Различают следующие виды упругих ударов: абсолютно упру­гий, абсолютно неупругий и реальный удар. После абсолютно неуп­ругого удара взаимодействующие тела движутся с общей скоростью, а их полная механическая энергия не сохраняется. Часть механиче­ской энергии переходит во внутреннюю энергию и в энергию оста­точной деформации. Удар абсолютно упругий и удар абсолютно не­упругий - это два предельных типа удара.

Для решения задачи о нахождении скоростей соударяющихся тел после взаимодействия (удара) воспользуемся законами сохране­ния энергии и импульса, так как решение этой задачи с помощью уравнений движения, требует знания зависимости сил, возникающих при ударе от времени. Законы сохранения импульса и энергии дают возможность написать два уравнения, в которые входят (в случае удара двух тел) две неизвестные величины - скорости тел после удара:

(4.1)

(4.2)

Решая систему этих уравнений, можно найти (зная начальные условия) скорости тел после удара. Вывод формул, по которым можно найти скорости тел после удара для случая упругого уда­ра, сделать самостоятельно при подготовке к работе.

Величина, определяемая формулой:

(4-3)

называется коэффициентом восстановления, который характеризует степень не упругости удара. Так для абсолютно упругого удара k=1, для абсолютно неупругого удара k=0, во всех остальных случаях (реальный удар) 0<k<1.

Величину средней силы удара можно найти на основании вто­рого закона Ньютона:

(4-4)

или в проекции на ось X:

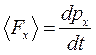(4-5)

Таким образом, для определения величины средней силы необ­ходимо знать изменение импульса взаимодействующего шара и время взаимодействия.

Время взаимодействия в данной работе определяется методом конденсаторного хронометра, основанного на измерении заряда, ко­торый успевает протечь через цепь баллистического гальванометра за время, подлежащее измерению. В течение этого времени через цепь гальванометра разряжается конденсатор, предварительно заря­женный до напряжения U₀. Шары при ударе замыкают электриче­скую цепь, составленную из конденсатора, магазина сопротивле­ний, соединенных между собой последовательно. Напряжение на обкладках конденсатора измеряется с помощью электростатическо­го вольтметра. (Значение емкости конденсатора указано на уста­новке, а величину сопротивления и начального напряжения на об­кладках конденсатора задает преподаватель). После замыкания цепи напряжение на обкладках конденсатора изменяется по закону

(4-6),

где U - напряжение на конденсаторе после первого удара, R - со­противление цепи баллистического гальванометра, C - емкость кон­денсатора, U₀ — начальное напряжение на конденсаторе. Из формулы (4-6) следует, что время удара можно найти по формуле:

(4-7).

Для определения изменения импульса необходимо знать скорость шара до удара и после удара. Для вывода расчетной формулы воспользуемся законом сохранения полной механической энергии. На основании закона сохранения энергии получаем:

для опускающегося шара

для поднимающегося шара

где V₁ - скорость ударяющего шара, U₁ и U₂ - скорости шаров после соударения, h₁ - высота подъема центра масс ударяющего шара, h^{`</sup><sub>1</sub> и h<sup>`}₂ - высоты подъема центра масс шаров после соударения.

Поскольку на установке непосредственно можно измерить уг­лы, на которые отклоняются шары после удара, и угол на который был отведен шар, то скорости шаров можно определить из соотно­шений

где L - расстояние от точки подвеса до центра тяжести шаров, a - угол, на который был отведен один из шаров, b и g - углы, на кото­рые разошлись шары после соударения, по отношению к положению равновесия. Величину L можно достаточно точно определить, если воспользоваться формулой для периода математического маятника.

Описание установки: Конструктивно установка (см. рис.1) представляет собой основание, на котором смонтирована стойка, не­сущая устройство подвески шаров. Устройство подвеса шаров мож­но перемещать в горизонтальном направлении и тем самым изме­нять межцентровое расстояние между шарами. Перемещение в вер­тикальном направлении осуществляется с помощью наматывающего барабана, укрепленного на устройстве подвеса шаров.

Для отсчета положения шаров имеются две шкалы, проградуированные в градусной мере. На шкале можно укреплять электромаг­нит, который служит для удержания одного из шаров в исходном положении. Перед началом эксперимента необходимо отцентро­вать всю систему, а также расположить начало шкал для отсче­та углов точно под центром шаров.

Рис. 1

Список заданий:

Задание 1:Определить, на какие углы отклонятся шары после удара, счи­тая удар абсолютно упругим. Результаты вычислений прове­рить экспериментально и занести в таблицу. Рассмотреть два случая:

а) большой шар бьет по маленькому шарику, который покоит­ся;

б) маленький шар бьет по большому шару, который покоится.

Задание 2: Экспериментально определить время взаимодействия шаров и рассчитать силу удара.

Задание 3:Считая удар реальным, определить коэффициент восстановле­ния. Необходимые данные взять из задания 1.

ЛАБОРАТОРНАЯ РАБОТА №5

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ».

Цель работы: изучение гармонического колебательного движения.

Вопросы для допуска к работе:

1. Что называют колебаниями? Какие колебания называются свободными гармоническими колебаниями?

2. При каких условиях возникают гармонические колебания?

3. Каким уравнением описываются гармонические колебания?

4. Что называют амплитудой, частотой, циклической частотой, фазой, начальной фазой, периодом гармонических колебаний? В каких единицах измеряются эти величины?

5. Какие колебания называются затухающими? При каких условиях они возникают?

6. Каким уравнением описываются затухающие колебания?

7. Что называют коэффициентом затухания, логарифмическим декрементом затухания, добротностью затухающих колебаний? В каких единицах измеряются эти величины?

8. Чем определяется период затухающих колебаний?

9. Что называют математическим маятником?

10. Чем определяется период математического маятника?

11. Что называют физическим маятником?

12. Чем определяется период физического маятника?

13. Что называют приведенной длиной физического маятника?

14. Что называется моментом инерции твердого тела, относительно неподвижной оси?

15. Как рассчитать момент инерции физического маятника, состоящего из диска, закрепленного на стержне?

16. Как определить расстояние от точки подвеса до центра масс физического маятника, состоящего из диска, закрепленного на стержне?

17. От чего зависит кинетическая, потенциальная и полная энергии тела, совершающего гармоническое колебательное движение?

Список рекомендуемой литературы:

Основная

1. Савельев И.В. Курс общей физики. - М., 1962, т.1, с. 176 -190.

2. Сивухин Д.В. Общий курс физики: Т.1. Механика. - М., 1974. (гл. 6), с. 204-215.

3. Яворский Б.И., Пинский А.А. Основы физики. - М., 1972, т.2, с. 185-190.

Дополнительная

1. Берклеевский курс физики: Т.1. Механика. - М., 1975, с. 219 -246.

Краткая теория

Гармоническими колебаниями называются такие движения, ко­торые описываются уравнениями или 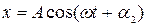, где х - смещение материальной точки от положения равновесия, - циклическая частота, показы­вающая число колебаний, совершаемых материальной точкой за 2p единиц времени; А - амплитуда, характеризующая наибольшее возможное смещение колеблющейся точки от положения равновесия; ( 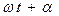) - фаза колебания, позволяющая определить, где нахо­дится в данный момент времени материальная точка, куда движет­ся, сколько полных колебаний совершила до рассматриваемого мо­мента; a₁ и a₂ - постоянные (начальные фазы), зависящие от условий в начальный момент отсчёта; Т - период.

Скорость материальной точки, совершающей гармоническое колебательное движение описыва­емое уравнением , зависит от времени следующим образом:

Ускорение:

.

Ускорение материальной точки, совершающей гармоническое колебательное движение, пропорцио­нально смещению и направлено в противоположную сторону (нахо­дится в противофазе). Из этого следует, что рассматриваемое движение материальной точки происходит под действием силы про­порциональной смещению. К таким силам, в первую очередь, относятся упругие силы, которые пропорциональны смещению х и направ­лены в противоположную ему сторону: .

Силы не упругие по своей природе, но аналогичные им по виду зависимости от смещения, называются квазиупругими.

Напишем уравнение движения материальной точки, на которую действуют упругие или квазиупругие силы: (1). Итак, 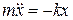или 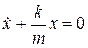.(В случае квазиупругих сил под "k" будем понимать коэффициент, объединяющий все постоянные величины в выражении силы, дейст­вующей на систему, выведенную из положения равновесия). Если 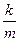обозначить через w², то уравнение (1) можно переписать (1'). 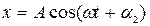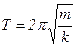Решение уравне­ния (1') имеет вид , или (убедитесь с помощью подстановки, что эти решения удовлетворяют уравнению (1)), где (2), откуда следует (3). Равенство (3) позволяет рассчитать период для различных гармонических колебательных движений, обусловленных упругими и квазиупругими силами.

Амплитуда А и начальная фаза не могут быть определены из дифференциального уравнения. Эти постоянные определяются началь­ными условиями, например, начальными значениями смещения х и скорости .

Совершающая колебания материальная точка обладает скоростью, а, следовательно, и кинетической энергией. Кроме того, колеблющаяся точка будет обладать и потенци­альной энергией. . Полная энергия .