Основные свойства корреляционной функции

1. При равенстве аргументов

2. Корреляционная функция симметрична относительно своих аргументов

3. Модуль корреляционной функцииy не превосходит произведение среднеквадратичных отклонений соответствующих сечений

Нормированная корреляционная функция (аналог - коэффициент корреляции ).

Свойства нормированной корреляционной функции следуют из свойств корреляционной функции:

1) При равенстве аргументов

2)

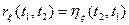
3)

Взаимной корреляционной функцией двух СП и 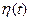называется неслучайная функция

,

которая при каждой паре 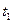и 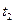равна корреляционному моменту двух сечений СП 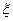и .

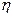Свойства взаимной корреляционной функции.

1) В общем случае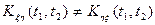

2)

Нормированная взаимная корреляционная функция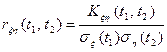

СП называется некоррелированными, если их взаимная корреляционная функция .

Стационарные и эргодические процессы [4]

Наиболее важное свойство СП, позволяющее применить разработанные и апробированные методы исследования – это независимость свойств СП от начала отсчета времени отсчета времени, т.е. стационарность.

СП называется стационарным в узком смысле, если многомерные законы распределения не меняются при сдвиге всех временных переменных на одно и то же число:

.

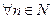
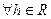Одномерная функция распределения для стационарного процесса в узком смысле не зависит от времени.

Двумерная функция распределения для стационарного процесса в узком смысле зависит только от интервала между сечениями.

Для многих СП n-мерный закон распределения практически невозможно найти, но во многих прикладных задачах это и не нужно, описание ряда СП можно осуществить в рамках корреляционной теории.

Более обширный класс - стационарные процессы, стационарные в широком смысле (по Хинчину). Чаще всего под стационарностью понимается стационарность в широком смысле.

СП называется стационарным в широком смысле если:

,

,

.

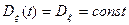Теорема. Из стационарности в узком смысле вытекает стационарность в широком смысле. (обратное утверждение в общем случае не верно)

Некоторые свойства корреляционной функции стационарного процесса.

1. .

2. .

3. .

Пример

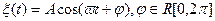
Стационарный случайный процесс называется периодическим с периодом , если его корреляционная функция является периодической функцией с этим периодом.

Теорема. Если — стационарный периодический случайный процесс с периодом , то его реализации с вероятностью являются периодическими с тем же периодом.

Эргодические процессы [1,4]

Самыми важными (по прикладному значению) из стационарных процессов для нас являются эргодические. Стационарный СП называется эргодическим, если для него осреднение по ансамблю реализаций может быть заменено осреднением по времени по одной реализации. Т.е. по любой одной достаточно длинной реализации мы можем судить о свойствах всех реализаций СП.

Процесс может быть эргодическим относительно математического ожидания и корреляционной функции. Чаще всего под эргодичностью понимается эргодичность в относительно математического ожидания.

Процесс является эргодическим относительно математического ожидания, если существует

,

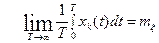не зависящий от выбора реализаций. В противном случае процесс не является эргодическим.

Достаточное условие эргодичности по математическому ожиданию (теорема Слуцкого):

.

Следствие:Если

, (*)

то случайный процесс является эргодическим.

Пример. Определить является ли случайный процесс с эргодическим по математическому ожиданию.

Заметим, что (*) не выполняется

.

Однако

.

Следовательно, случайный процесс является эргодическим по математическому ожиданию.

Процесс является эргодическим по отношению к корреляционной функции, если существует

,

не зависящий от выбора реализаций.