Решение дифференциальных уравнений
9.5.1 Решить дифференциальное уравнение на отрезке [ 0; 1 ] .
y¢’ =2· y + e x - x y( 0 ) = 0.25
Построить график решения, на котором дополнительно точками отобразить функцию  .
.
9.5.2 Решить систему дифференциальных уравнений на отрезке [ 1; 2 ] .
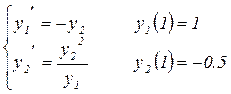
Построить графики решения y1(x), y2(x) , на этом же рисунке дополнительно отобразить точками график функции:  .
.
9.5.3 Решить дифференциальное уравнение на отрезке [ 1; 2 ] .
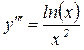
y( 1 ) = 0; y’ ( 1 ) = 1; y ‘’( 1 ) =2
Показать решение на графике, Отобразить точками на этом же графике функцию 
9.5.4 Решить систему дифференциальных уравнений:

где 
l = 0.25;
a = p /4;
0 £ t £ 12
Построить зависимости x( t); y (t); y (x).
9.5.5 Найти решение дифференциального уравнения только в одной точке
x =1.2
y''= x· exp(x)
y(0) = 1; y'(0) = 0 .
9.5.6 Найти решение дифференциального уравнения, удовлетворяющее заданным краевым условиям:
y''- y = 0; y(0) = 0; y(2·p) = 1.
Показать решение графически. На этом же графике показать точками функцию
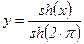 .
.
9.5.7 Найти решение дифференциального уравнения, удовлетворяющее заданным краевым условиям, в одной единственной точке x = 0.6
y'' + y = 0; y ‘ (0) = 0; y'(1) = 1.
Статистические задачи
9.6.1 В файле D:\WORK\STAT.PRN записан массив чисел.
а) считать этот массив в MathCad и определить:
- число элементов в массиве;
- минимальный Xmin и максимальный Xmax элементы массива;
- среднее, медиану, дисперсию и среднеквадратичное отклонение чисел массива;
б) показать элементы массива на графике в виде точек;
в) разбить диапазон (Xmax - Xmin) на 10 равных интервалов и построить гистограмму распределения частот попаданий считанных величин в соответствующие интервалы;
г) в предположении, что считанные величины подчиняются нормальному закону распределения, построить на том же графике теоретическую кривую распределения с параметрами, найденными в пункте а).
9.6.2 Вычислить вероятность того, что случайная величина, имеющая стандартное нормальное распределение ( µ = 0; σ = 1 ), превосходит 1.0 .
9.6.3 Определить плотность распределения вероятности в точке 5.5 случайной величины, имеющей распределение ХИ-квадрат с числом степеней свободы 11.
9.6.4 Создать вектор 1000 случайных величин, имеющих равномерное распределение на отрезке [ 0; 2 ] . Построить гистограмму распределения полученных значений, состоящую из 20 столбцов. На этом же графике показать линию, соответствующую теоретическому распределению.
Символьные вычисления
9.7.1 При помощи символьного знака равенства аналитически вычислить:
а) 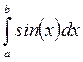 б)
б) 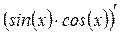
в)  г)
г) 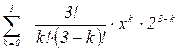
9.7.2 При помощи символьного знака равенства и соответствующего ключевого слова упростить:
а)  б)
б) 
в) 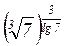 г)
г) 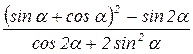
9.7.3 При помощи символьного знака равенства и ключевого слова expand раскрыть скобки в выражении, а затем, с помощью ключевого слова factor вернуться к исходному выражению
а)  б)
б) 
9.7.4 Разложить функцию f(x) в ряд Тейлора в окрестности точки x0, используя члены со степенью, меньше n:
а) f(x) = cos (x) x0 = 0; n = 6
б) f(x) = ln (1 + x) x0 = 0; n = 4
в) f(x) = sh(x) x0 = 1; n = 6
г) f(x)= sin (x) x0 = p /2; n = 4
9.7.5 Выполнить задание 9.7.2. с использованием меню Символы.
9.7.6 Выполнить задание 9.7.3. с использованием меню Символы.
9.7.7 Привести подобные члены в выражении, используя меню Символы
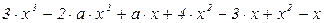
9.7.8 Разложить на элементарные дроби выражение

9.7.9 С помощью меню Символы c найти производные f ‘(x) и упростить полученные выражения:
а) 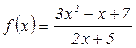 б)
б) 
9.7.10 С помощью меню Символы вычислить неопределенные интегралы и упростить полученные выражения;
а) 
б) 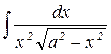
в) 
9.7.11 Решить уравнения:
а) 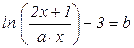
б) 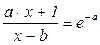
в) 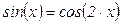
9.7.12 Решить неравенства:
а) 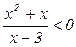 б)
б) 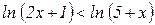
9.7.13 Заменить в выражении 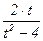 переменную t на x + 3 и полученное выражение разложить на элементарные дроби.
переменную t на x + 3 и полученное выражение разложить на элементарные дроби.
Составление программ
9.8.1 Написать программу вычисления количества отрицательных, положительных и нулевых элементов вектора.
9.8.2 Составить программу вычисления произведения четных положительных чисел, меньших заданного n.
9.8.3 Для заданных a, b, d получить вектор, содержащий числа a, a + d, d +2d, ..., b. Например, если a = 1, b = 2, d = 0.2, то искомый вектор должен содержать числа 1, 1.2, 1.4, 1.6, 1.8, 2.
9.8.4 Получить вектор из n наименьших целых положительных чисел, делящихся хотя бы на одно из заданных натуральных a, b.
9.8.5 Написать программу, результатом работы которой должна быть единичная матрица порядка n.
9.8.6 Преобразовать натуральное число в вектор, компонентами которого являются десятичные цифры числа.
9.8.7 Выполнить преобразование, обратное описанному в задаче 9.8.6.
9.8.8 Перемешать случайным образом компоненты вектора.
9.8.9 Написать программу для нахождения пересечения двух множеств чисел, содержащихся в векторах V и W.
9.8.10 С помощью рекурсивного определения функции написать программу вычисления сложных процентов: какова будет сумма вклада через n лет, если начальный вклад VH, и годовой процент - PROC.
9.8.11 Написать программу вычисления корня уравнения f(x) = 0 с точностью ε методом половинного деления.
9.8.12 Составить программу нахождения корня уравнения f(x) = 0 с точностью ε методом касательных.
ЛИТЕРАТУРА
1 Литература основная:
1.1 Дьяконов В.П. Книга Энциклопедия Mathcad 2001i и Mathcad 11. "Солон-Пресс", 2004. - 832 с.
1.2 Кирьянова Д. Mathcad 11.Самоучитель С-Пб: БХВ-Петербург, 2003. - 538 с.
1.3 Кудрявцев Е.М. Справочник по Mathcad 11. Издательство: ДМК Пресс, 2005. -184 с.
1.4 Плис А. И. Mathcad: Математический практикум для инженеров и экономистов: учеб. пособие / А. И. Плис, Н. А. Сливина. 2 е изд., перераб. и доп. М. : Финансы и статистика, 2003. - 656 с. : ил.
2 Литература дополнительная
2.1 MathCAD 6.0 Plus. Финансовые, инженерные и научные расчеты в среде Windows 95./Перевод с англ. - М.: Информационно издательский дом “Филинъ”, 1996. – 712 с.: ил.
2.2 Дьяконов В. Mathcad 2000 : учеб. курс / В. Дьяконов. СПб. : Питер, 2001. - 592 с. : ил.
2.3 Дьяконов В.П., Абраменкова И.В. MathCad Pro в математике, физике и Internet, М.: Нолидж: 2000, 512 с.: ил.
2.4 Дьяконов В.П. Справочник по MathCad 7.0 Pro.-М.:СК-ПРЕСС.-1998.-352 с.
2.5 Дьяконов В.П. Компьютерная математика. Теория и практика. М.: Нолидж, 2001. – 1296 с., ил.
2.6 Очков В.Ф. MathCad 7 Pro для студентов и инженеров.-М.: Компьютер ПРЕСС.- 1998.- 384 с.: ил.
2.7 Очков В.Ф. MathCad 8 Pro для студентов и инженеров.-М.:Компьютер ПРЕСС.-1999.- 523 с.:ил.
2.8 Поршнев С. В. Компьютерное моделирование физических процессов с использованием пакета MathCAD : учеб. пособие / С. В. Поршнев. - М. : Горячая линия : Телеком, 2002. - 252 с.
2.9 Поршнев С. В. Вычислительная математика. Курс лекций. СПб.: БХВ-Петербург, 2004. - 320 с.: ил.
2.10 Поршнев С.В., Беленкова И.В. Численные методы на базе MATHCAD. –СПб.: БХВ-Петербург, 2005. – 464 с.: ил.
2.11 Плис А. И. Mathcad 2000 : Математический практикум для экономистов и инженеров : учеб. пособие / А. И. Плис, Н. А. Сливина. М. : Финансы и экономика, 2000. - 656 с. : ил.
2.12 Плис А.И., Сливина Н.А. Mathcad 2000. –М.: Финансы и статистика, 2000.-656 с.
3 Методические пособия
3.1 Николаев Н.А. Решение задач в системе MathCAD 2000. Методическое пособие. - Новоуральск, НПИ МИФИ, 2003. - 68 с. :ил.
3.2 Тихонова Е.В. Введение в MathCad. Методическое пособие. Новоуральск, НТИ НИЯУ МИФИ, 2012, - 80 с.
4 Обучающие системы и электронная документация (каталог EDUCATION сервера кафедры )
4.1 Mathcad. User’s Guide. Mathcad 2000 Professional. Техническая документации, поставляемая с пакетом (англ.).
Файл Z:\EDUCATION\MathCad\Mathcad.pdf.
4.2 Электронный учебник по работе в MathCAD 7 PRO.
Файл Z:\EDUCATION\MathCad\MathCAD 7 PRO - электронный учебник.chm
4.3 Электронный учебник по работе в MathCAD 12.
Файл Z:\EDUCATION\MathCad\MathCAD 12 - электронный учебник.chm
УДК 681.3.06
Автор Тихонова Евгения Валерьевна
РЕШЕНИЕ ЗАДАЧ В СИСТЕМЕ MATHCAD
Методическое пособие по курсам «Информатика»,
«Решение инженерных задач на ЭВМ»,
«Вычислительные методы в инженерных расчетах»
для преподавателей и студентов всех специальностей
очной, очно-заочной форм обучения.
Новоуральск, НТИ НИЯУ МИФИ, 2013. - 75 с.
Сдано в печать Формат А5 Бумага писчая
Печать плоская Уч.-изд.л. 2.4 Тираж 50 экз.
Заказ Издательство НТИ Лицензия ИД №00751 г. Новоуральск, Ленина, 85
