Ковариационная матрица двумерной непрерывной случайной величины,коэффициенткорреляции,пределызначений,доказательство;независимость и некоррелированность:понятие и признаки. 1 страница
Компонентами ковариационной матрицы являются центральные моменты компонент случайного вектора: вторые центральные моменты и ковариации. Математическое определение ковариационной матрицы:
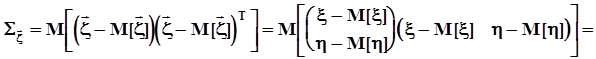
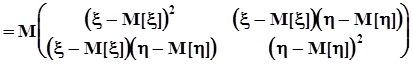 .Математическое ожидание случайной матрицы есть матрица, каждый элемент которой есть математическое ожидание соответствующего элемента исходной случайной матрицы. В итоге ковариационная матрица двумерного случайного вектора приобретает вид
.Математическое ожидание случайной матрицы есть матрица, каждый элемент которой есть математическое ожидание соответствующего элемента исходной случайной матрицы. В итоге ковариационная матрица двумерного случайного вектора приобретает вид 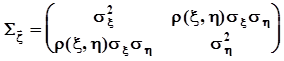 .Как видно, это симметричная квадратная матрица, ее размер соответствует размерности исходного случайного вектора. Определитель этой матрицы вычисляется достаточно просто:
.Как видно, это симметричная квадратная матрица, ее размер соответствует размерности исходного случайного вектора. Определитель этой матрицы вычисляется достаточно просто:
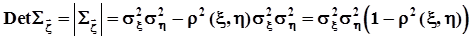 .Если случайные компоненты вектора
.Если случайные компоненты вектора  независимы или хотя бы некоррелированы, ковариационная матрица становится диагональной, а ее определитель равен произведению диагональных элементов:
независимы или хотя бы некоррелированы, ковариационная матрица становится диагональной, а ее определитель равен произведению диагональных элементов:

 .При взаимнооднозначной связи между x и h ,например, линейной
.При взаимнооднозначной связи между x и h ,например, линейной  ,коэффициент корреляции
,коэффициент корреляции  , а из этого следует, что определитель ковариационной матрицы равен нулю, то есть в этом случае матрица оказывается особенной. Этого следовало ожидать, поскольку если между составляющими случайного вектора существует взаимнооднозначная связь, то, по сути дела, существует всего одна случайная величина, случайный вектор вырождается в скалярную (одноразмерную) случайную величину, и ковариационная матрица содержит только один элемент, то есть также вырождается в скаляр, а именно, в значение дисперсии.Для представления степени взаимной зависимости между компонентами случайного вектора применяется корреляционная матрица, элементами которой являются коэффициенты корреляции:
, а из этого следует, что определитель ковариационной матрицы равен нулю, то есть в этом случае матрица оказывается особенной. Этого следовало ожидать, поскольку если между составляющими случайного вектора существует взаимнооднозначная связь, то, по сути дела, существует всего одна случайная величина, случайный вектор вырождается в скалярную (одноразмерную) случайную величину, и ковариационная матрица содержит только один элемент, то есть также вырождается в скаляр, а именно, в значение дисперсии.Для представления степени взаимной зависимости между компонентами случайного вектора применяется корреляционная матрица, элементами которой являются коэффициенты корреляции: 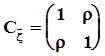 .Если компоненты случайного вектора независимы или хотя бы некоррелированы, корреляционная матрица становится единичной матрицей. Для того, чтобы избавиться от масштаба значений, принимаемых случайными величинами, в качестве показателя линейной зависимости используется частное от деления ковариации на произведение среднеквадратических значений случайных величин:
.Если компоненты случайного вектора независимы или хотя бы некоррелированы, корреляционная матрица становится единичной матрицей. Для того, чтобы избавиться от масштаба значений, принимаемых случайными величинами, в качестве показателя линейной зависимости используется частное от деления ковариации на произведение среднеквадратических значений случайных величин: 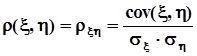 .Эта величина называется коэффициентом корреляции. Случайные величины, у которых коэффициент корреляции равен нулю, называются некоррелированными. Независимые случайные величины с необходимостью некоррелированы. Обратное, вообще говоря, неверно! Из некоррелированности случайных величин их независимость, вообще говоря, не следует. Это понятно хотя бы потому, что из равенства нулю центрального смешанного момента порядка 1, 1 вовсе не следует, что все центральные смешанные моменты более высоких порядков также равны нулю.Определим максимально возможное значение коэффициента корреляции. Естественно предположить, что своего максимального значения коэффициент корреляции достигает при взаимно однозначной связи между x и h,например, линейной
.Эта величина называется коэффициентом корреляции. Случайные величины, у которых коэффициент корреляции равен нулю, называются некоррелированными. Независимые случайные величины с необходимостью некоррелированы. Обратное, вообще говоря, неверно! Из некоррелированности случайных величин их независимость, вообще говоря, не следует. Это понятно хотя бы потому, что из равенства нулю центрального смешанного момента порядка 1, 1 вовсе не следует, что все центральные смешанные моменты более высоких порядков также равны нулю.Определим максимально возможное значение коэффициента корреляции. Естественно предположить, что своего максимального значения коэффициент корреляции достигает при взаимно однозначной связи между x и h,например, линейной  .Для этого случая нам известна ковариация междуx и h, а из п. 1.6.5 следует, что
.Для этого случая нам известна ковариация междуx и h, а из п. 1.6.5 следует, что  , то есть
, то есть 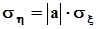 . В результате получаем:
. В результате получаем:  ,а это означает, что
,а это означает, что 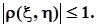
21.Двумерные непрерывные случайные величины,условные плотности распределения,признак независимости,формула полной вероятности, формула Байеса,характеристическая функция;характеристическая функция и плотность распределения суммы двух независимых случайных величин.условную функцию распределения, то есть функцию распределения одной из случайных величин при условии, что другая случайная величина принимает некоторое конкретное значение, например,
 |
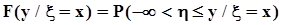 .Выделим на координатной плоскости область, показанную на рис. 24.
.Выделим на координатной плоскости область, показанную на рис. 24.
Вероятность того что случайный вектор принимает значения из этой области, равна  . В соответствии с формулой для условной вероятности из п. 1.2.3
. В соответствии с формулой для условной вероятности из п. 1.2.3  .Условная функция распределения получается в результате предельного перехода:
.Условная функция распределения получается в результате предельного перехода: 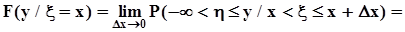
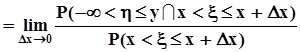
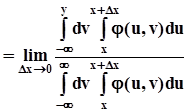 .По теореме о среднем, внутри интервала
.По теореме о среднем, внутри интервала 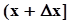 найдется точка
найдется точка  , такая, что
, такая, что 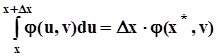 ,
,
поэтому 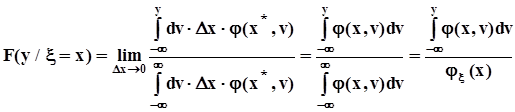 .Условная плотность распределения есть производная от условной функции распределения:
.Условная плотность распределения есть производная от условной функции распределения:  .Аналогично
.Аналогично  .Обычно обозначают
.Обычно обозначают 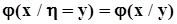 и
и  . В этих обозначениях из полученных формул следует:
. В этих обозначениях из полученных формул следует:  ,
, 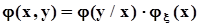 С учетом полученных соотношений перепишем формулы для маргинальных распределений в виде:
С учетом полученных соотношений перепишем формулы для маргинальных распределений в виде: 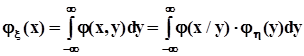 ,
, 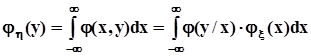 .Это формулы полной вероятности для непрерывных случайных величин.Поскольку
.Это формулы полной вероятности для непрерывных случайных величин.Поскольку  =
= 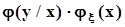 , получаем формулу Байеса для непрерывных случайных величин:
, получаем формулу Байеса для непрерывных случайных величин: 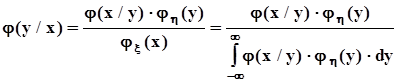 .Если x и h независимы, то
.Если x и h независимы, то  ,
,  и поэтому
и поэтому  .Справедливо и обратное,если
.Справедливо и обратное,если  , то следует независимость x и h.Признак независимости случайных величин: 2 случайные величины независимы, когда их совместная плотность распределения может быть представлена, как произведение маргинальных плотностей распределения этих величин.Характеристическая функция двумерного случайного вектора. Двумерный случайный вектор
, то следует независимость x и h.Признак независимости случайных величин: 2 случайные величины независимы, когда их совместная плотность распределения может быть представлена, как произведение маргинальных плотностей распределения этих величин.Характеристическая функция двумерного случайного вектора. Двумерный случайный вектор  задан плотностью распределения j(x,y) и в результате “испытаний” может принимать значения
задан плотностью распределения j(x,y) и в результате “испытаний” может принимать значения  .Обозначение и математическое определение характеристической функции вектора
.Обозначение и математическое определение характеристической функции вектора  :
:  ,где
,где 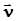 - двумерный вектор, с компонентами
- двумерный вектор, с компонентами 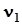 и
и 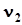 .В соответствии с математическим определением мат.ожидания
.В соответствии с математическим определением мат.ожидания  .Св-а характеристических ф-й двумерного вектора:
.Св-а характеристических ф-й двумерного вектора: 

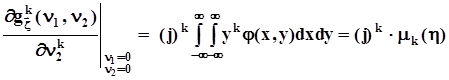 ,
, 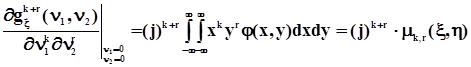 .К этим свойствам добавляется еще одно. Пусть x и h - независимы, и y = x + h. Тогда
.К этим свойствам добавляется еще одно. Пусть x и h - независимы, и y = x + h. Тогда 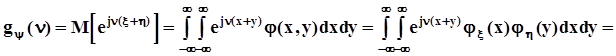
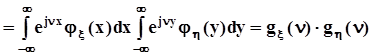 ,то есть, характеристическая функция суммы независимых случайных величин равна произведению характеристических функций этих величин .Плотность распределения суммы двух независимых случайных величин Поскольку xиhнезависимы, совместная плотность распределения j(x,y) =
,то есть, характеристическая функция суммы независимых случайных величин равна произведению характеристических функций этих величин .Плотность распределения суммы двух независимых случайных величин Поскольку xиhнезависимы, совместная плотность распределения j(x,y) = 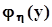 .Сделаем замену x = z - y: j(z - y,y) =
.Сделаем замену x = z - y: j(z - y,y) = 
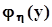 и найдем маргинальную плотность распределения
и найдем маргинальную плотность распределения  .Если сделать замену y = z - x ,получим
.Если сделать замену y = z - x ,получим 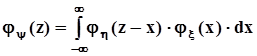 .Если y = x + hи величины xиhнезависимы, то характеристическая функция их суммы - произведение характеристических функций слагаемых
.Если y = x + hи величины xиhнезависимы, то характеристическая функция их суммы - произведение характеристических функций слагаемых 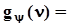
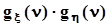 . Прямое преобразование Фурье этого произведения- есть свертка плотностей распределения слагаемых:
. Прямое преобразование Фурье этого произведения- есть свертка плотностей распределения слагаемых:  .Применительно к плотностям распределения эту операцию иногда называют композицией.
.Применительно к плотностям распределения эту операцию иногда называют композицией.
22.Многомерные случайные величины,функцияраспределения и плотность распределения,моменты,ковариационнаяматрица,формулы для мат ожидания и ковариационной матрицы линейной функции от случайного вектора: y=Ax+b.
Многомерная случайная величина (случайный вектор)
случайный вектор и его компоненты греческими буквами, а значения, которые они принимают, - латинскими: 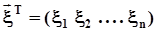 ,
, 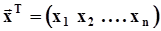 .Функция распределения и плотность распределения многомерного случайного вектора определяются по аналогии с такими же характеристиками двумерного вектора
.Функция распределения и плотность распределения многомерного случайного вектора определяются по аналогии с такими же характеристиками двумерного вектора 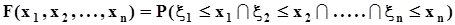
 .
.
Начальные моменты k - го порядка 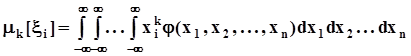 ,центральные моменты k - го порядка
,центральные моменты k - го порядка 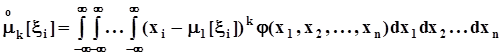 . В частности мат ожидания и дисперсии i - ых компонент:
. В частности мат ожидания и дисперсии i - ых компонент: 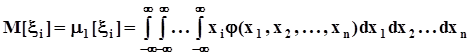
 . Из бесчисленного количества комбинаций смешанных моментов запишем только ковариации, то есть центральные смешанные моменты порядка 1, 1:
. Из бесчисленного количества комбинаций смешанных моментов запишем только ковариации, то есть центральные смешанные моменты порядка 1, 1: 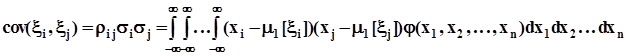 ,где
,где  - коэффициент корреляции компонент
- коэффициент корреляции компонент 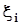 и
и  ,
, 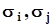 - среднеквадратические значения этих компонент.Мат ожидание, ковариационная и корреляционная матрицы многомерного случайного вектора суть
- среднеквадратические значения этих компонент.Мат ожидание, ковариационная и корреляционная матрицы многомерного случайного вектора суть 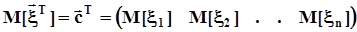 ,
, 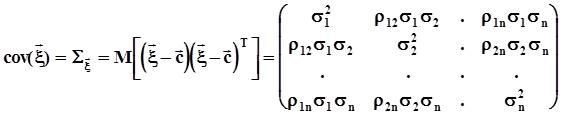 ,
,
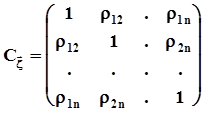 .Эти обе матрицы симметричны и неотрицательно определены.Если компоненты вектора независимы или хотя бы некоррелированы, то матрицы диагональны, а корреляционная матрица есть единичная матрица.
.Эти обе матрицы симметричны и неотрицательно определены.Если компоненты вектора независимы или хотя бы некоррелированы, то матрицы диагональны, а корреляционная матрица есть единичная матрица.
Маргинальные (частные) и условные плотности распределения могут быть многомерными: 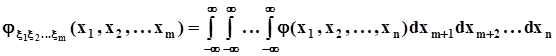 ,
,
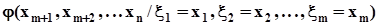
 ,где m = 1, 2, . . . , n - 1. Характеристическая функция многомерного случайного вектора записывается в векторном виде так:
,где m = 1, 2, . . . , n - 1. Характеристическая функция многомерного случайного вектора записывается в векторном виде так:  ,где вектор
,где вектор 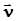 есть
есть 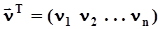 . Мат ожидание и ковариационная матрица вектора
. Мат ожидание и ковариационная матрица вектора 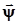 , который получается в результате линейного преобразования вектора
, который получается в результате линейного преобразования вектора 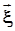 :
:  выражаются формулами:
выражаются формулами:  ,
, 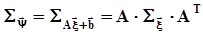 .Многомерная нормальная плотность распределения имеет вид:
.Многомерная нормальная плотность распределения имеет вид: 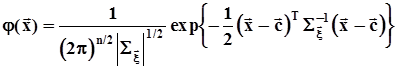 .Сечения этой поверхности плоскостями
.Сечения этой поверхности плоскостями 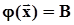 суть многомерные эллипсоиды.Принадлежность случайного вектора n - мерному нормальному распределению будем обозначать, как
суть многомерные эллипсоиды.Принадлежность случайного вектора n - мерному нормальному распределению будем обозначать, как 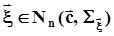 .
.
23. Двумерное нормальное распределение,плотность распределения вероятностей,моменты и ковариационная матрица,характеристическаяфункция.Многомерный нормальный случайный вектор,плотность распределения. Двумерная нормальная плотность распределенияВновь обозначим: 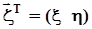 - нормальный случайный вектор,
- нормальный случайный вектор, 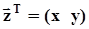 - значения, которые он принимает. Двумерная нормальная плотность распределения записывается в виде
- значения, которые он принимает. Двумерная нормальная плотность распределения записывается в виде  где
где  - двумерный вектор - математическое ожидание случайного вектора
- двумерный вектор - математическое ожидание случайного вектора  ,
, 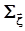 - ковариационная матрица вектора
- ковариационная матрица вектора  ,
,  - ее определитель.
- ее определитель.  ,
,  ,
,  .В дальнейшем принадлежность случайного вектора двумерному нормальному распределению будем обозначать, как
.В дальнейшем принадлежность случайного вектора двумерному нормальному распределению будем обозначать, как 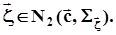 Форма и свойства двумерной нормальной плотности распределения определяются, в основном, показателем степени экспоненты и не зависят от ее расположения, а потому положим
Форма и свойства двумерной нормальной плотности распределения определяются, в основном, показателем степени экспоненты и не зависят от ее расположения, а потому положим  . В связи с этим рассмотрим показатель степени экспоненты отдельно:
. В связи с этим рассмотрим показатель степени экспоненты отдельно:  .Обращение матрицы выполним через алгебраические дополнения и определитель:
.Обращение матрицы выполним через алгебраические дополнения и определитель: 
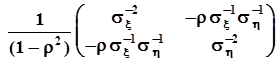 .Тогда
.Тогда 
 .Если нормальные случайные величины xиhнекоррелированы, то есть r = 0, то показатель степени экспоненты упрощается очевидным образом, и двумерная нормальная плотность распределения распадается на два сомножителя:
.Если нормальные случайные величины xиhнекоррелированы, то есть r = 0, то показатель степени экспоненты упрощается очевидным образом, и двумерная нормальная плотность распределения распадается на два сомножителя: 
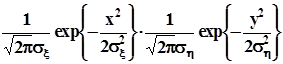 ,
,
Из некоррелированности двух нормально распределенных случайных величин с необходимостью следует их независимость; это исключительное свойство нормальных случайных величин, которое является их характеризационным признаком, а именно, если для двух случайных величин установлено, что из некоррелированности следует их независимость, то эти случайные величины распределены нормально.
24.Геометрическая интерпретация ковариационнойматрицы,коэффициента корреляции и среднеквадратических значений компонент нормального случайного вектора. Проанализируем геометрическую форму поверхности, которая задана нормальной плотностью распределения. Эта поверхность имеет max в точке  , т.к. при любом отклонении от этой точки абсолютная величина показателя степени экспоненты возрастает, а из-за того, что этот показатель степени <0, ф-я в целом убывает. Значение max в указанной точке = множителю перед экспонентой.Для исследования формы поверхности положим
, т.к. при любом отклонении от этой точки абсолютная величина показателя степени экспоненты возрастает, а из-за того, что этот показатель степени <0, ф-я в целом убывает. Значение max в указанной точке = множителю перед экспонентой.Для исследования формы поверхности положим  и рассечем ее плоскостью, параллельной плоскости x0y на уровне B, ниже max значения. Указанное рассечение выражается равенством
и рассечем ее плоскостью, параллельной плоскости x0y на уровне B, ниже max значения. Указанное рассечение выражается равенством 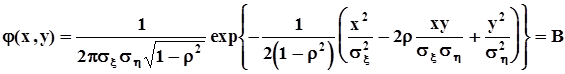 .В сечении получим фигуру, описываемую уравнением
.В сечении получим фигуру, описываемую уравнением  .Обозначим
.Обозначим  , тогда уравнение фигуры, получившейся в сечении, принимает знакомый вид:
, тогда уравнение фигуры, получившейся в сечении, принимает знакомый вид: 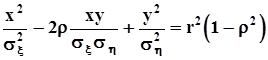 ,
,
 |
Это ур-е эллипса, размеры и расположение которого определяются его параметрами: радиусом  , который увеличивается с уменьшением B, то есть с приближением секущей плоскости к плоскости x0y, длинами полуосей
, который увеличивается с уменьшением B, то есть с приближением секущей плоскости к плоскости x0y, длинами полуосей  и
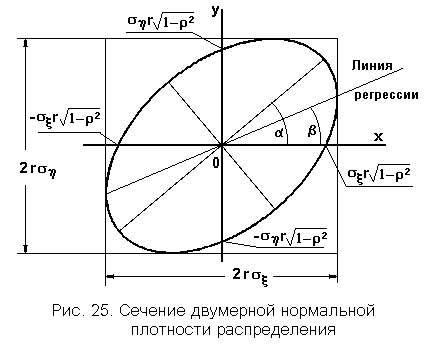
и  , а также коэффициентом корреляции r. Пример одного из сечений приведен на рис. 25. Непосредственно из уравнения эллипса видно, что точки его пересечения с осями координат суть
, а также коэффициентом корреляции r. Пример одного из сечений приведен на рис. 25. Непосредственно из уравнения эллипса видно, что точки его пересечения с осями координат суть 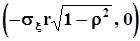 ,
, 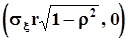 - с осью ‘x’ и
- с осью ‘x’ и 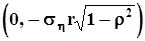 ,
, 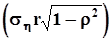 - с осью ‘y’. Угол наклона большой оси к оси абсцисс равен
- с осью ‘y’. Угол наклона большой оси к оси абсцисс равен 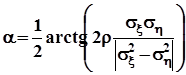 .При изменении коэффициента корреляции в диапазоне от -1 до 1 все эллипсы остаются вписанными в прямоугольник со сторонами
.При изменении коэффициента корреляции в диапазоне от -1 до 1 все эллипсы остаются вписанными в прямоугольник со сторонами 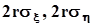 . При r = 0оси эллипса совпадают с осями координат, при r = -1и при r = +1точки его пересечения с осями перемещаются в начало координат, и эллипс вырождается в прямую линию.
. При r = 0оси эллипса совпадают с осями координат, при r = -1и при r = +1точки его пересечения с осями перемещаются в начало координат, и эллипс вырождается в прямую линию.
25.Условные нормальные плотности распределения,ихпараметры,уравнение регрессии и характеризационноесвойствонормальных случайных величинлиния регрессии. Эта линия есть геометрическое место точек, которые представляют все условные математические ожидания M[h/x=x].Для того, чтобы получить уравнение этой линии, найдем выражение для условной плотности распределения, для чего воспользуемся соответствующей формулой из п. 1.7.1, памятуя о том, что маргинальные плотности двумерного нормального распределения также нормальны 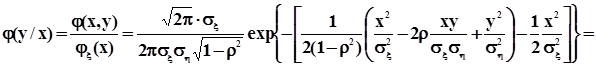
 .В фигурных скобках имеет место полный квадрат разности, поэтому
.В фигурных скобках имеет место полный квадрат разности, поэтому  .Полученное выражение есть каноническая запись одномерной нормальной плотности распределения с параметрами:- дисперсия равна
.Полученное выражение есть каноническая запись одномерной нормальной плотности распределения с параметрами:- дисперсия равна 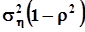 ,- математическое ожидание равно
,- математическое ожидание равно 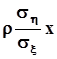 .Таким образом, мы получили условную плотность распределения, которая оказывается также нормальной, и условное математическое ожидание
.Таким образом, мы получили условную плотность распределения, которая оказывается также нормальной, и условное математическое ожидание 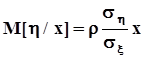 , которое является линейной функцией x . Напомним, что в начале настоящего пункта мы положили равными нулю математические ожидания обеих компонентов случайного вектора
, которое является линейной функцией x . Напомним, что в начале настоящего пункта мы положили равными нулю математические ожидания обеих компонентов случайного вектора  . Настало время вспомнить об этом и записать условное математическое ожидание для общего случая:
. Настало время вспомнить об этом и записать условное математическое ожидание для общего случая:
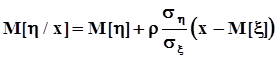 .Полученное выражение называется уравнением линейной регрессии случайной величины h на случайную величину x. Угол наклона линии регрессии к оси абсцисс есть
.Полученное выражение называется уравнением линейной регрессии случайной величины h на случайную величину x. Угол наклона линии регрессии к оси абсцисс есть 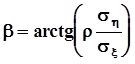 .Регрессия между двумя нормальными случайными величинами (если она существует, то есть когда r¹ 0) всегда линейна. Это естественно, поскольку только линейное преобразование не изменяет вид плотности распределения.Прямая регрессии обязательно проходит через середины вертикальных хорд эллипса, потому что условные нормальные распределения, которые являются сечениями двумерной плотности вертикальными плоскостями, симметричны, и их математические ожидания совпадают с модами и медианами этих сечений. И потому прямая регрессии пересекается с эллипсом в точках касания вертикальных касательных к нему.
.Регрессия между двумя нормальными случайными величинами (если она существует, то есть когда r¹ 0) всегда линейна. Это естественно, поскольку только линейное преобразование не изменяет вид плотности распределения.Прямая регрессии обязательно проходит через середины вертикальных хорд эллипса, потому что условные нормальные распределения, которые являются сечениями двумерной плотности вертикальными плоскостями, симметричны, и их математические ожидания совпадают с модами и медианами этих сечений. И потому прямая регрессии пересекается с эллипсом в точках касания вертикальных касательных к нему.
Предмет и задачи математической статистики, исходные понятия, предварительная обработка выборочных данных (кондиционирование результатов): вариационный ряд, выборочная функция распределения, гистограмма.2.1. Задачи математической статистики
Основными задачами математической статистики являются:1. Определение числовых характеристик, параметров и свойств случайных величин по результатам экспериментов .2. Проверка статистических гипотез о числовых характеристиках, параметрах и свойствах случайных величин по результатам экспериментов .Все значения, которые может принимать случайная величина x, образуют генеральную совокупность X. При выполнении экспериментов из генеральной совокупности извлекаются значения 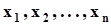 ,которые называются выборочными значениями, а массив выборочных значений называется выборкой. Кол-во выборочных значений n - объем выборки. В ряде случаев нам будет удобно обозначать выборку с помощью вектора выборочных значений
,которые называются выборочными значениями, а массив выборочных значений называется выборкой. Кол-во выборочных значений n - объем выборки. В ряде случаев нам будет удобно обозначать выборку с помощью вектора выборочных значений 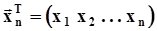 , где индекс ‘n’ обозначает объем выборки, то есть размерность этого вектора.Пусть F(x), j(x) - функция распределения и плотность распределения случайной величины x. В дальнейшем мы будем называть их, а также их числовые характеристики и параметры генеральной функцией распределения, генеральной плотностью распределения, генеральными числовыми характеристиками и генеральными параметрами соответственно. Оценки функции распределения, плотности распределения, числовых характеристик и параметров, полученные по выборочным значениям, мы будем называть выборочными.В математической статистике принято, что все эксперименты выполняются таким образом, чтобы выборочные значения были независимыми в смысле определения независимости. Поэтому в дальнейшем мы будем предполагать, что эксперимент организован таким образом, чтобы это условие обеспечивалось. В дальнейшем нам придется говорить о случайности выборочных значений и соответственно - о случайности оценок характеристик и параметров, полученных путем обработки выборочных значений. Противоречивость ситуации состоит в следующем. С одной стороны, выборочные значения, которые получены в результате эксперимента, суть реализации значений, принятых случайной величиной, и уже не являются случайными. С другой стороны, при повторении n экспериментов выборочные значения будут другими. То есть выборочные значения и вектор выборочных значений являются функциями случайных событий. Поэтому в дальнейшем мы будем считать выборочные значения случайными на множестве групп экспериментов объемом nкаждая, выполняемых в одних и тех же неизменных заранее обусловленных условиях. В терминах и аксиоматике, это означает, что в качестве элементарного события
, где индекс ‘n’ обозначает объем выборки, то есть размерность этого вектора.Пусть F(x), j(x) - функция распределения и плотность распределения случайной величины x. В дальнейшем мы будем называть их, а также их числовые характеристики и параметры генеральной функцией распределения, генеральной плотностью распределения, генеральными числовыми характеристиками и генеральными параметрами соответственно. Оценки функции распределения, плотности распределения, числовых характеристик и параметров, полученные по выборочным значениям, мы будем называть выборочными.В математической статистике принято, что все эксперименты выполняются таким образом, чтобы выборочные значения были независимыми в смысле определения независимости. Поэтому в дальнейшем мы будем предполагать, что эксперимент организован таким образом, чтобы это условие обеспечивалось. В дальнейшем нам придется говорить о случайности выборочных значений и соответственно - о случайности оценок характеристик и параметров, полученных путем обработки выборочных значений. Противоречивость ситуации состоит в следующем. С одной стороны, выборочные значения, которые получены в результате эксперимента, суть реализации значений, принятых случайной величиной, и уже не являются случайными. С другой стороны, при повторении n экспериментов выборочные значения будут другими. То есть выборочные значения и вектор выборочных значений являются функциями случайных событий. Поэтому в дальнейшем мы будем считать выборочные значения случайными на множестве групп экспериментов объемом nкаждая, выполняемых в одних и тех же неизменных заранее обусловленных условиях. В терминах и аксиоматике, это означает, что в качестве элементарного события 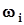 мы будем рассматривать исход одного эксперимента, результатом которого является получение выборочного вектора
мы будем рассматривать исход одного эксперимента, результатом которого является получение выборочного вектора  . В таких условиях это случайный n-мерный вектор с независимыми одинаково распределенными компонентами, т.к. все выборочные значения в соответствии с соглашениями, принятыми в математической статистике, извлечены из одной генеральной совокупности. Вероятностная мера на этом множестве порождена вероятностной мерой, которая определена генеральной совокупностью исследуемой случайной величины x .
. В таких условиях это случайный n-мерный вектор с независимыми одинаково распределенными компонентами, т.к. все выборочные значения в соответствии с соглашениями, принятыми в математической статистике, извлечены из одной генеральной совокупности. Вероятностная мера на этом множестве порождена вероятностной мерой, которая определена генеральной совокупностью исследуемой случайной величины x .
