Определитель Вронского набора функций. Теорема об определителе Вронского набора функций на отрезке.
Вопросы к теоретическому тесту 2
По дисциплине Дифференциальные уравнения
По материалу параграфа 7- начало параграфа 13 лекций
Вопросы, выделенные жирным шрифтом, нужно знать с доказательством.
1. Общее и линейное дифференциальные уравнения (ДУ) 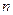 -го порядка. Однородное и неоднородное линейные ДУ.
-го порядка. Однородное и неоднородное линейные ДУ.
2. Постановка задачи Коши для линейного ДУ 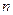 -го порядка. Теорема о существовании и единственности ее решения.
-го порядка. Теорема о существовании и единственности ее решения.
3. Линейность дифференциального оператора 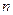 -го порядка. Принцип суперпозиции.
-го порядка. Принцип суперпозиции.
4. Линейная независимость и линейная зависимость набора функций на отрезке.
Определитель Вронского набора функций. Теорема об определителе Вронского набора функций на отрезке.
6. Теорема об определителе Вронского набора решений линейного однородного ДУ 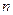 -го порядка. Ее следствие – «альтернатива Вронского».
-го порядка. Ее следствие – «альтернатива Вронского».
7. Фундаментальная система решений (ФСР) линейного однородного ДУ 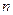 -го порядка. Способ построения ФСР.
-го порядка. Способ построения ФСР.
8. Теорема о ФСР линейного однородного ДУ 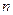 -го порядка с переменными коэффициентами.
-го порядка с переменными коэффициентами.
9. Теорема об общем решении линейного неоднородного ДУ 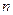 -го порядка. Ее геометрическая интерпретация.
-го порядка. Ее геометрическая интерпретация.
10. Метод вариации постоянных для нахождения частных решений линейного неоднородного ДУ 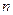 -го порядка.
-го порядка.
11. Формула Коши для решения линейного неоднородного ДУ 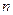 -го порядка с нулевыми начальными данными.
-го порядка с нулевыми начальными данными.
12. Линейное ДУ 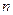 -го порядка с постоянными коэффициентами. Его характеристический многочлен.
-го порядка с постоянными коэффициентами. Его характеристический многочлен.
13. Лемма о тождестве, связывающем линейный дифференциальный оператор 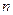 -го порядка с постоянными коэффициентами с его характеристическим многочленом.
-го порядка с постоянными коэффициентами с его характеристическим многочленом.
14. Теорема о явном виде ФСР линейного ДУ 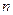 -го порядка с постоянными коэффициентами.
-го порядка с постоянными коэффициентами.
15. Замечание о виде вещественной ФСР линейного ДУ 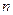 -го порядка с постоянными коэффициентами.
-го порядка с постоянными коэффициентами.
16. Теорема о частных решениях линейного ДУ 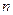 -го порядка с постоянными коэффициентами с правыми частями специального вида.
-го порядка с постоянными коэффициентами с правыми частями специального вида.
17. Замечание о вещественных частных решениях линейного ДУ 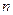 -го порядка с постоянными коэффициентами с вещественными правыми частями специального вида.
-го порядка с постоянными коэффициентами с вещественными правыми частями специального вида.
18. Уравнения Эйлера. Их сведение к ДУ с постоянными коэффициентами.
19. Уравнение Бесселя порядка  . Обобщенный степенной ряд.
. Обобщенный степенной ряд.
20. Функция Бесселя порядка  .
.
21. Функция Бесселя порядка 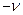 при нецелом
при нецелом  . ФСР уравнения Бесселя при нецелом
. ФСР уравнения Бесселя при нецелом  .
.
22. Система нелинейных ДУ. Постановка задачи Коши. Векторная запись.
23. Система линейных ДУ. Теорема о свойствах решения задачи Коши для нее.
24. Метод Пикара для систем линейных ДУ и его свойства.
25. Сведение линейного ДУ 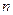 -го порядка к системе ДУ. Приложение к задаче Коши.
-го порядка к системе ДУ. Приложение к задаче Коши.
26. Теорема о глобальной разрешимости задачи Коши для системы нелинейных ДУ.
27. Теорема о локальной разрешимости задачи Коши для нелинейной системы ДУ. Теорема Пеано.
28. Линейная зависимость и линейная независимость вектор-функций на отрезке.
