Моделирование нормально распределенной случайной величины

Большое число статистических задач связано с анализом последовательностей значений нормально распределенных случайных величин, называемых нормальными случайными числами. Последовательность нормальных случайных чисел не может быть получена стандартным методом моделирования, поскольку функция распределения нормального закона распределения (функция Лапласа) не выражается через элементарные функции. Наиболее распространенный способ получения нормальных случайных чисел из последовательности равномерных основан на использовании центральной предельной теоремы теории вероятностей.

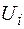Рассмотрим сумму , где - независимые равномерно распределенные на отрезке 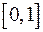случайные величины, имеющие математические ожидания и дисперсии .

В соответствии с центральной предельной теоремой случайная величина

имеет приближенно нормальное распределение с параметрами (приближение тем лучше, чем больше ). На практике удовлетворительное приближение к нормальному распределению 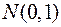получается уже при и это значение параметра обычно используют для конкретных вычислений. Таким образом, из последовательности равномерных случайных чисел можно получить последовательность нормальных случайных чисел 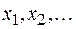с параметрами по формуле:

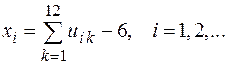
Если есть необходимость в получении нормальных случайных чисел с параметрами , то следует положить .

Приведенный алгоритм получения нормальных случайных чисел прост в реализации, однако он приводит лишь к приближенно нормальным случайным числам. Кроме того, он имеет существенный недостаток в смысле быстродействия процесса моделирования, так как для получения одного нормального случайного числа используется равномерных случайных чисел.

Другой метод получения нормальных случайных чисел из равномерных, часто используемый на практике, состоит в построении соответствующего явно вычисляемого функционального преобразования. Пример такого преобразования дает следующее утверждение.

Утверждение(см. [5, разд. 2.12]). Пусть случайные величины 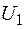и являются независимыми и распределенными равномерно на отрезке 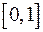. Тогда случайные величины

,

являются независимыми и имеют стандартное нормальное распределение .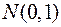

Доказательство этого утверждения представляет собой простое упражнение в вычислении плотности вероятностей при взаимнооднозначном преобразовании случайных векторов. Якобиан указанного преобразования равен

.

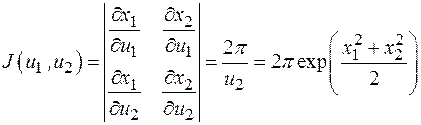Поэтому совместная плотность вероятностей величин 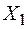и равна

.

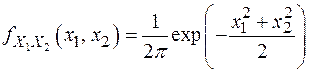Таким образом, каждая пара равномерных случайных чисел с помощью указанного в утверждении преобразования порождает пару нормальных 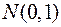случайных чисел .

Приведенным алгоритмом предпочтительно пользоваться, когда необходимо получить достаточно много нормальных чисел, так как он требует существенно меньше равномерных случайных чисел. Следует отметить также, что нормальные случайные числа, получаемые с его помощью, являются более точными, нежели полученные с помощью центральной предельной теоремы.