Доверительные интервалы. Доверительная вероятность

Основные понятия и определения.

Современная статистикаразрабатывает планирование эксперимента, занимается последующим анализом и др.

Если требуется изучить совокупность однородных объектов относительно некоторого признака, то на практике не изучают каждый элемент, а случайно отбирают ограниченное число объектов и изучают их.

Выборкой называют совокупность случайно отобранных объектов.

Генеральной называется совокупность объектов, из которых производится выборка.

Объем совокупности – это число объектов этой совокупности.

Наиболее удобно выборку записывать в виде таблицы:

х1	х2	…	xk
n1	n2	…	nk

где наблюдаемые значения х_i называются вариантами (каждое из х_i наблюдалось n_i раз), а указанная последовательность вариант, записанных в возрастающем порядке называется вариационным рядом, n_i – частоты.

Статистические оценки параметров. Точечные оценки.

Пусть θ – неизвестный оцениваемый параметр, а θ^* - приближенное значение данного параметра, полученное на основании выборочных данных.

Такая оценка θ^* параметра θ в виде одного числа, называется точечной оценкой.

Точечная оценка называется несмещенной, если М(θ^*) = θ , и смещенной - в противном случае.

Точечная оценка называется эффективной, если ее дисперсия минимальна среди всех других возможных оценок данного параметра.

Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки ее значение неограниченно приближается к оцениваемому параметру.

Несмещенной, эффективной и состоятельной оценкой мат. ожидания изучаемого признака является выборочная средняя:

,

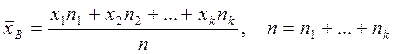где n– объем выборки.

Если объем всей генеральной совокупности равен N, а количественный признак может принимать отдельные изолированные значения, то математическое ожидание

.

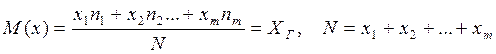Точечная оценка дисперсии – выборочная дисперсия:

.

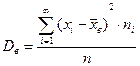Для расчетов можно применять и другую формулу:

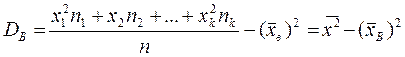
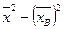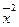Доказательство: D_B= , где вычисляют по формуле: .

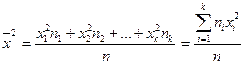Выборочная дисперсия является смещенной оценкой, поэтому при малых значениях объема выборки применяют исправленную выборочную дисперсию: .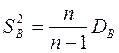

Выборочное среднее квадратическое отклонение- смещенная оценка генерального среднего квадратического отклонения:

.

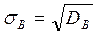Исправленное выборочное среднее квадратическое отклонение:

-

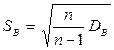несмещенная оценка генерального среднего квадратического отклонения.

где n=n₁ + n₂ +…+n_k – объем выборки.

Условные варианты. Моменты. Метод произведений

Предположим, что варианты выборки расположены в возрастающем порядке, причем – равноотстоящие, т.е. те, которые образуют арифметическую прогрессию с разностью h = x_i+1 – x_i – шаг выборки (при этом условные варианты будут целыми числами).

Условными называют варианты, которые определяются равенством 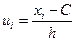, где С – ложный ноль (новое начало отсчета). В качестве ложного нуля можно взять любую варианту, но максимальная простота вычислений достигается, если она находится примерно в середине вариационного ряда и имеет наибольшую частоту.

Замечание: если С = х_m, то u_m=0.

Обычным эмпирическим моментом порядка k называется величина 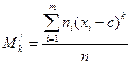, где n_i – частоты, x_i – значения вариант, с – некоторое значение, n – объем выборки. В частности, .

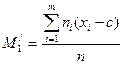Начальным эмпирическим моментом порядка k называется обычный момент порядка k при с=0: 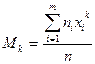. В частности,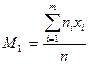

Замечание:очевидно, что М₁ = .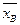

Центральным эмпирическим моментом порядка k называется обычный момент порядка k при c= 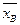: 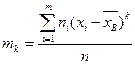. В частности, .

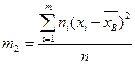Замечание:очевидно, что m₂ = D_B.

Теорема1: m₂ = M^/₂ – (M^/₁)².

Условным эмпирическим моментом порядка k называется начальный момент порядка k, вычисленный для условных вариант: .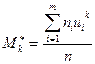

Теорема2: если С – ложный ноль, h – шаг выборк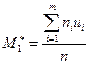и, и 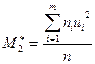- условные эмпирические моменты соответственно 1^го и 2^го порядков, то выборочная средняя равна 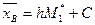, выборочная дисперсия: .

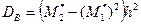Метод произведений применяется для вычисления условных моментов, следовательно, и для вычисления 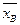и 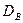. Для простоты вычислений целесообразно воспользоваться расчетной таблицей вида:

хi	ni	ui	niui	niu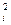

1. В 1^ом столбце записывают выборочные (первоначальные) варианты в возрастающем порядке.

2. Во 2^ом - записывают частоты этих вариант.

3. В 3^ем – записывают условные варианты 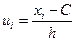(практически, в клетках над u_i=0 по порядку пишут числа -1, -2, -3, …, а в клетках под ним – числа 1, 2, 3, …

4. В 4^ом – вычисляют произведения n_iu_i.

5. В 5^ом – вычисляют произведения n_iu .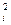

6. Далее суммируют вычисления по столбцам, записывая результаты снизу.

7. Вычисляют условные моменты 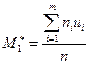, 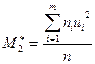и выборочные среднюю 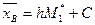, дисперсию 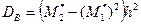и среднее квадратическое отклонение s_В = .

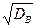Замечание: можно добавить 6^ой столбец, в котором вычисляют произведения n_i(u_i+1)². Внизу, просуммировав, получают 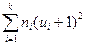. Если 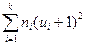= 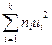+ 2 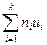+ n, то вычисления произведены правильно.

Пример. Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х_i, а во второй строке – соответственные частоты n_i количественного признака Х). Требуется найти:

1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение.

2. Доверительный интервал для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.

хi
ni

Решение: 1. Для нахождения 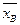и D_В методом произведений составим расчетную таблицу (в качестве ложного нуля выбираем С=280, т.е. u₃=0, значит, u₂= -1, u₁= -2, u₄=1, u ₅ = 2, u₆ = 3, u₇ = 4):

хi	ni	ui	niui	niu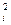
		-2	-10
		-1	-15

Вычислим условные моменты: 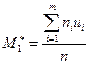= =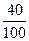0,4; 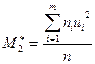= =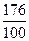1,76.

Теперь, зная ложный ноль С=280 и шаг выборки h=270 – 260 =10, вычисляем выборочную среднюю: 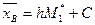=10×0,4+280=284; выборочную дисперсию: 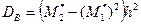= (1,76 – 0,4²)×10² = 160; выборочное среднее квадратическое отклонение: s_В = 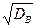= 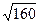»12,65.

2. Доверительный интервал.

D_В=160 Þ s= 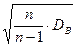= 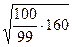» 12,71.

Пользуясь таблицей приложения 3 по g = 0,95 и n = 100 находим t_g=1,984, тогда искомый доверительный интервал 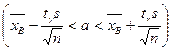примет вид: 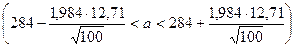, т.е. .

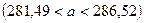Ответ: 1. а) 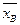=284, б) s_В =12,65; 2. .

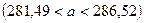Доверительные интервалы. Доверительная вероятность

Интервальной называют оценку неизвестного параметра, которая определяется двумя числами – концами интервалов.

Доверительной вероятностью называется вероятность того, что точечная оценка параметра отклонится по модулю от оцениваемого параметра не более, чем на заданное значение δ:

.

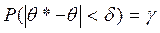Значение γ называют надежностью оценки.

Неравенство 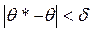задает доверительный интервал:

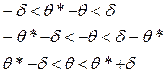
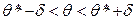- интервальная оценка параметра θ или доверительный интервал, в который с вероятностью γ попадает истинное значение оцениваемого параметра.

Задача 1. Дано: Х – количественный признак, распределенный нормально;

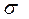– среднее квадратическое отклонение.

Найти: доверительный интервал для М(Х)=а.

Будем рассматривать выборочную среднюю 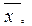как случайную величину (так как она меняется от выборки к выборке);

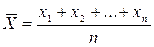
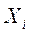- распр. нормально, с 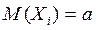и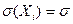

Тогда (по доказанному выше) М( 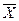)=а,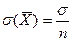

P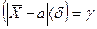

P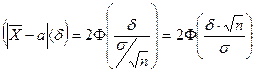

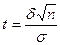найдем по таблице функции Лапласа: =>

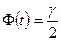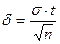
Итак, доверительный интервал для математического ожидания нормально распределенной случайной величины Х в случае известного среднего квадратического отклонения:

,

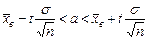δ – среднее квадратическое отклонение;

n – объем выборки;

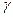- надежность;

t – аргумент интегральной функции Лапласа, такой, что .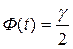

Задача 2. Дано: Х - распределено нормально;

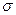- неизвестно.

Найти: доверительный интервал для М(Х)=а

Случайная величина 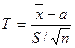имеет распределение Стьюдента с k=n-1 степенями свободы;

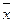- выборочная средняя;

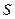– «исправленное» среднее квадратическое отклонение,

n – объем выборки.

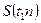- плотность распределение Стьюдента, определяется параметром n (не зависит от а и σ).

=

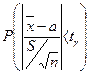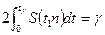
Параметр 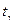можно найти по таблице распределения Стьюдента для заданных n и γ.

Итак, доверительный интервал для математического ожидания нормально распределенной случайной величины Х в случае неизвестной дисперсии:

,

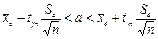Задача 3. Оценить вероятность появления события А по относительной частоте.

Пусть произведено 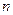независимых испытаний с неизвестной вероятностью появления события А в каждом испытании.

Точечные оценки математического ожидания и дисперсии для случайной величины 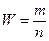соответственно равны:

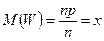и .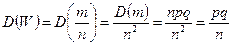

Если n достаточно велико, то 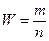распределена приближенно нормально.

;

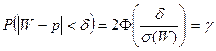
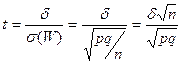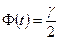=> t по таблице функции Лапласа: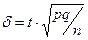

Если w>p, то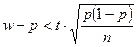

Возведем в квадрат обе части неравенства, преобразуем выражение, получим квадратное неравенство относительно неизвестной вероятности .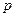

Тогда 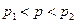, где корни квадратного трехчлена

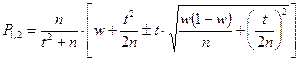
Доверительный интервал для вероятности:

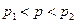
Замечание. Если известно распределение Х, но неизвестны его параметры, то для их определения используют метод моментов Пирсона.

Приравнивают теоретические моменты к соответствующим эмпирическим моментам, и находят из полученной системы уравнений неизвестные параметры.