Глава 9. Численное интегрирование

Существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подынтегральная функция заменяется «близкой» к ней функцией, интеграл от которой выражается через элементарные функции.

Формула прямоугольников

Если известны значения функции f(x) в некоторых точках x₀, x₁, … , x_m, то в качестве функции «близкой» к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

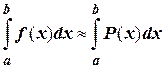
Разобьем отрезок интегрирования [a; b] на n равных частей. Обозначим длину каждой части 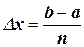. При этом y₀ = f(x₀), y₁ = f(x₁), …., y_n = f(x_n).

Составим суммы: y₀Dx + y₁Dx + … + y_n-1Dx

y₁Dx + y₂Dx + … + y_nDx

Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной.

Тогда

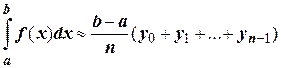
или 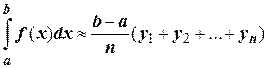(9.1)

любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.

Формула трапеций

Эта формула является более точной по сравнению с формулой прямоугольников. Подынтегральная функция в этом случае заменяется на вписанную ломаную.

Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций (рис. 9.1). Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.

Площади вписанных трапеций вычисляются по формулам:

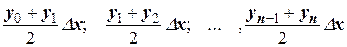
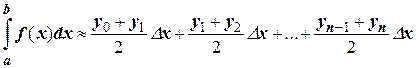
После приведения подобных слагаемых получаем формулу трапеций:

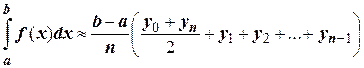(9.2)

Метод средних

Пусть для определенности a = x₀, b = x_n. Обозначим через 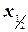, , 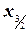, 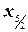… середины интервалов (x₀, x₁), (x₁, x₂), (x₂, x₃), … Полагаем 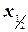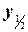f( 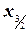) = 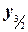, f( ) = , f( 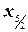) = 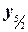, … . Тогда

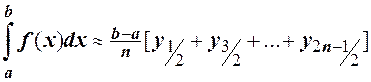(9.3)

Выражение (9.3)определяет площадь ступенчатой фигуры (риc. 8.3.1).

В большинстве случаев при данном n формула (9.3) точнее, чем (9.1) и (9.2). С увеличением n точность формул (9.1), (9.2), (9.3) неограниченно возрастает.

Формула Симпсона

(формула парабол или квадратурная формула)

Разделим отрезок интегрирования [a, b] на четное число отрезков п=2m. Площадь криволинейной трапеции, ограниченной графиком функции f(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями f(x₀), f(x₁), f(x₂).

Для каждой пары отрезков построим такую параболу (рис. 8.4.1).

Уравнения этих парабол имеют вид Ax² + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.

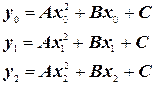(9.4)

Обозначим .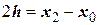

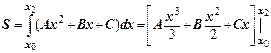
Если принять х₀ = –h, x₁ = 0, x₂ = h, то

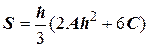(9.5)

Тогда уравнения значений функции (9.4) имеют вид:

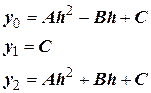
C учетом этого: .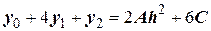

Отсюда уравнение (8.5.1) примет вид: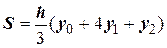

Тогда

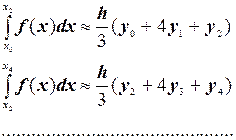
Складывая эти выражения, получаем формулу Симпсона:

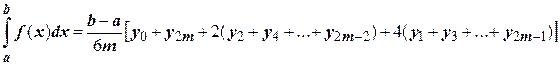
Чем больше взять число m, тем более точное значение интеграла будет получено.

Примеры

№1. Найти приближенное значение определенного интеграла 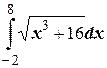с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей.

Решение.

Так как п=2т, то в нашем примере т=5. По формуле Симпсона получим:

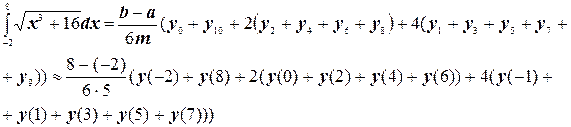
Все дальнейшие расчеты приведены в таблице:

i
xi	–2	–1
y(xi)	2,83	3,87		4,12	4,9	6,56	8,94	11,87	15,23	18,95	22,98

Окончательно получим,

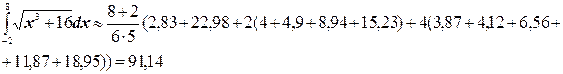
Точное значение этого интеграла – 91.173.

Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.

Абсолютная погрешность равна .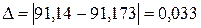

Относительная погрешность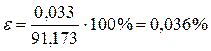

Для сравнения применим к этому же интегралу формулу трапеций.

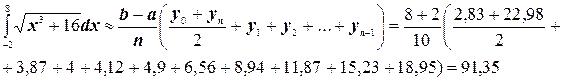
Абсолютная погрешность равна .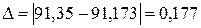

Относительная погрешность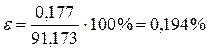

Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.

№2. Вычислить определенный интеграл 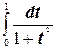с помощью формулы прямоугольников, если п=10.

Решение.

По формуле прямоугольников получим: .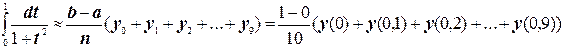

Резльтаты вычислений поместим в таблицу:

i
ti		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
y(ti)		0,99	0,96	0,92	0,86	0,80	0,74	0,67	0,61	0,55

Таким образом,

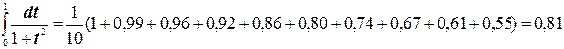.Точное значение этого интеграла – 0,79.

Найдем точное значение интеграла

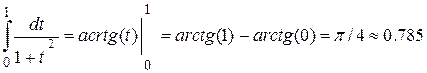
Абсолютная погрешность равна .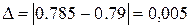

Относительная погрешность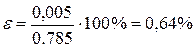

Вывод: формула прямоугольников для данного числа разбиений дала достаточно точный результат (погрешность меньше 1%).

№3. Найти площадь криволинейной трапеции, ограниченной графиком функции y = 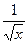и прямыми: y = 0, x = a = 1, x = b =11 методами:

а) прямоугольников;

б) трапеций;

в) Симпсона;

г) аналитическим с использованием формулы Ньютона-Лейбница.

Построить график заданной функции с разбиением отрезка 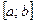на n = 10 подынтервалов и график функции 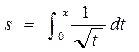на отрезке x .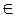

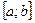Решение. Составим таблицу разбиения отрезка интегрирования на n = 10 равных участков с длинами интервалов Dx = 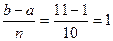(табл. 11.1). Во второй строке таблицы представлены увеличенные в 10 раз значения 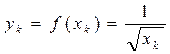(k = ).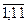

Таблица 9.1 Данные для численных методов

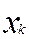	1 2 3 4 5 6 7 8 9 10 11
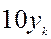	10 7,07 5,77 5,00 4,47 4,08 3,78 3,54 3,33 3,16 3,02

а) Используя формулу прямоугольников с высотами, представляющими собой левые значения функции на концах подынтервалов, найдем приближенное значение площади криволинейной трапеции в виде суммы площадей прямоугольников, очерченных на рис. 11.6 сплошными линиями:

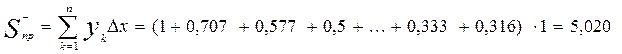
Та же формула прямоугольников, но с подстановкой в нее высот, равных правым значениям функции на концах подынтервалов, дает значение интеграла, равного площади ограниченных пунктиром прямоугольников:

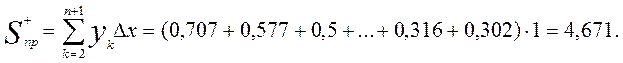
б) По формуле трапеции получим

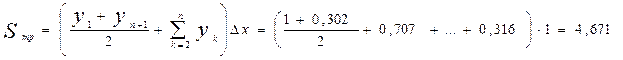
Следует обратить внимание на очевидное равенство

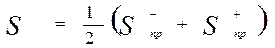
в) По формуле Симпсона (n=5–количество спаренных подынтервалов)

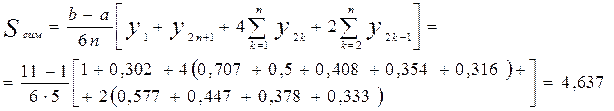
г) Определим точное значение интеграла, являющегося табличным:

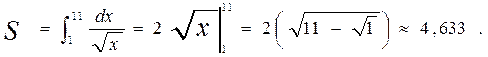
Найдем относительные ошибки определения площадей различными использованными методами численного интегрирования, сравнивая их с точным значением площади, полученным по формулам Ньютона-Лейбница:

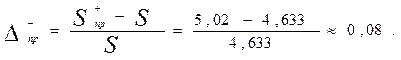
Аналогично:

;

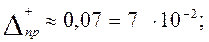
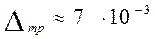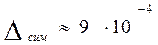
Варианты заданий

Для всех вариантов выполнить:

а). С помощью формул прямоугольников, трапеций и Симпсона вычислить интегралы при заданном числе разбиений.

б). Сравнить полученные результаты с точными значениями интегралов, найденными аналитически. Для каждого метода рассчитать значения абсолютной (D) и относительной (e) погрешностей вычислений.

Используемые формулы: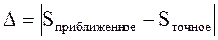

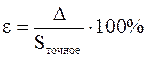
в). Сделать выводы о точности полученных результатов.

2. ;

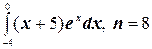3. ;

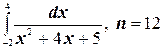4. ;

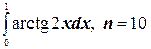5. ;

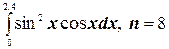6. ;

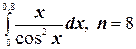7. ;

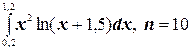8. ;

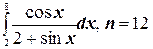9. ;

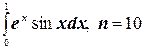10. ;

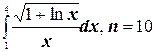11. ;

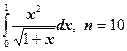12. ;

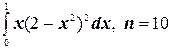13. ;

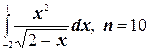14. ;

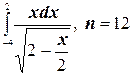15. .

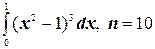Контрольные вопросы

1. Что такое первообразная? Обладают ли первообразные одной функции свойством единственности?

2. Дайте определение, в том числе в виде математического выражения, неопределенного интеграла.

3. Что такое подынтегральная функция? подынтегральное выражение?

4. В чем заключается метод замены переменной в определенном интеграле? Метод интегрирования по частям?

5. Что называется определенным интегралом?

6. Запишите формулу Ньютона-Лейбница.

7. В чем состоит геометрический смысл определенного интеграла? экономический смысл?

8. В чем суть применения метода прямоугольников при вычислении определенных интегралов? метода трапеций?

9. Какая аппроксимация подынтегральной функции осуществляется при выводе формулы Симпсона.

10. Могут ли результаты вычисления определенных интегралов по формулам трапеций или прямоугольников быть точнее результатов, полученных по формуле Симпсона?