Построение графиков функций

С помощью средств программной среды MathCADможностроитьграфики видов:

· двумерные

· трехмерные.

Рассмотрим построение двумерных графиков. Эту задачу можно решить двумя способами:

· путем использования интервальной переменной;

· путем использования интервальной переменной и переменной с индексами.

В первом случае сначала определяется функция. Для этого вводится имя функции, затем в скобках ее аргументы, далее оператор присваивания. После этого вводится ее алгебраическое выражение. После этих операций определенная таким образом функция может использоваться наравне со встроенными функциями. Например, введем параболическую функцию:

Заметим, что все параметры, входящие в функцию, должны быть заданы до определения функции.

Чтобы получить значение функции при определенном значении аргумента необходимо записать:

и т.д.

Для построения графика функции необходимо многократно вычислять ее значения при различных значениях аргумента. Для этого в программе MathCAD предусмотрено понятие интервальной переменной (по аналогии с понятием циклов в языках программирования). Синтаксис интервальной переменной имеет вид:

:=начальное значение[, начальное значение+шаг]..конечное значение

В скобках указан необязательный параметр шаг, по умолчанию равный 1. Двоеточие <..> вводится клавишей точка с запятой <;> или кнопкой <m..n> панели Матрица.

Допустим, что аргумент функции х изменяется на отрезке [-2;2] с шагом h=1. С помощью интервальной переменной это записывается следующим образом:

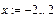
Чтобы получить значения аргумента (интервальной переменной), введем: х=. Для получения значений функции введем: f(x)=. Полученные значения аргумента и функции показаны на рисунке 1.

Рис.1

Для построения графика воспользуемся панелью Графика, в которой выберем

Х-У график. В маркере оси х укажем переменную х, в маркере оси у – переменную у. График будет иметь вид, показанный на рисунке 2.

Рис.2

Выделив график двойным щелчком, можно производить настройку графика, в частности выбрать тип, цвет, толщину линии и т.д. Можно, например, использовать опции графической панели:

· Zoom - позволяет выделить часть графика;

· Trace – отслеживает изменение координат на графике и т.д.

Пусть шаг изменения аргумента будет равен 0,1. Интервальная переменная в этом случае будет иметь вид:

Тогда график примет вид, показанный на рисунке 3.

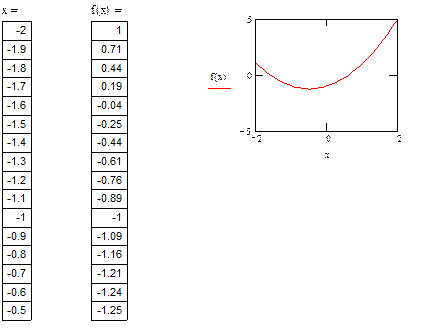
Рис. 3.

Чтобы просмотреть все значения функции и аргумента надо щелкнуть мышкой по соответствующей таблице и воспользоваться появившейся линейкой прокрутки.

Рассмотрим второй способ построения графиков – путем использования интервальной переменной и переменной с индексами. Построим тот же график этим способом.

Введем индекс как интервальную переменную:

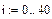
Определим x_i:

x_i:=-2+0,1+i

Вычислим:

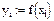
То есть, получим вектор-столбец значений функции. Введем х= и у=, получим матрицы. При помощи переменной с индексом созданы две одномерные матрицы с одним столбцом и 41-й строкой. Теперь строим график, где в качестве аргумента и функции следует указать переменные с индексом х_i и y_i.

На одном Х-У графике можно построить до 16 функций. Функции вводятся через запятую.

Аналогично можно использовать двумерную матрицу для построения графика функции двух переменных. Например, определим функцию от двух переменных и две интервальные переменные:

f(x,y):=x²-y²

i:=0..10 j:=0..10

Теперь определяем две переменные с индексом:

x_i:=-5+0,1+i y_j:=-5+0,1+j

Определим двумерную матрицу:

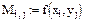
и построим поверхность, выбрав на панели Графика соответствующую кнопку. В качестве единственного аргумента графика укажем имя матрицы М.

Рис. 4. Рис. 5.

Изменив настройки можно получить другое изображение поверхности, как показано на рисунке 5. Для этого двойным щелчком мыши вызываем меню настройки и устанавливаем опции цвета, поворот -50 градусов и угол зрения 35.

Задания.

Построить график функции одной переменной двумя способами и график функции двух переменных. Интервал изменения аргументов от –5 до 4 с шагом 0,5. График функции одной переменной построить в декартовых и полярных координатах.

Номер варианта	Двумерный график	Трехмерный график
1.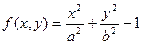
2.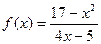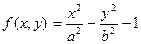
3.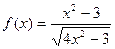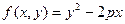
4.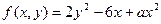
5.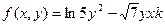
6.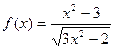
7.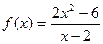
8.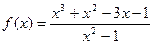
9.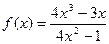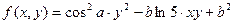
10.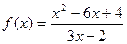
11.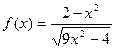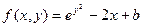
12.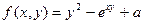
13.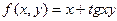
14.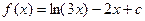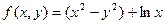
15.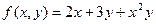
16.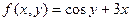
17.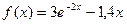
18.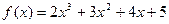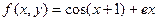
19.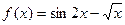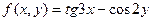
20.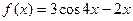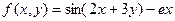
21.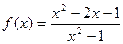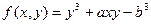
22.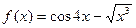

3.4 Решение уравнений и систем.

Для численного поиска корней уравнения в программе MathCAD используется функция root. Она служит для решения уравнений вида f(x) = 0, где f(x)— выражение, корни которого нужно найти, а x — неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: root (f(x),x). Здесь f(x) — функция перемен­ной х, используемой в качестве второго параметра. Функция root возвращает зна­чение независимой переменной, обращающее функцию f(x) в 0. Например:

х := 1

root(2-sin(x) – x,x) = 1,895.

Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения.

Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом функции find (найти). Между ними располагают «логические утверждения», задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения.

Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства — кнопка Логически равно на панели инструментов Логика. Другие знаки логических условий также можно найти на этой панели.

Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечислены искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных. Например:

х := 0 у := 0

given

x+y=1

х² + у²=4

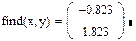
Задания.

Решить уравнение и систему уравнений, приведенных в таблице. Начальное значение х=0. Систему линейных уравнений решить двумя способами: методом, описанным выше и с помощью матриц коэффициентов С=А^-1×В. Выполнить проверку ответов с помощью подстановки.