Построение логарифмических частотных характеристик разомкнутой одноконтурной системы
Разомкнутая САУ в общем случае состоит из нескольких звеньев, имеющих свои передаточные функции. Передаточная функция всей САУ представляет собой произведение передаточных функций звеньев, как это видно из выражения (4.14). Поэтому выражение для ЛАХ разомкнутой системы в соответствии с (4.35):
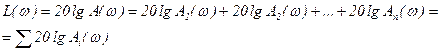 (4.39)
(4.39)
Таким образом, логарифмическая амплитудно-частотная характеристика разомкнутой системы может быть получена построением ЛАХ отдельных звеньев САР и последующим их суммированием.
В соответствии с выражением (4.35) ЛФХ разомкнутой системы строится аналогично.
Основное преимущество логарифмических частотных характеристик по сравнению с обычными – операции умножения при построении частотных характеристик заменяются суммированием, причем построение асимптотических логарифмических частотных характеристик оказывается достаточно простым.
Удобство использования асимптотических логарифмических характеристик состоит в том, что они состоят из отрезков прямых линий-асимптот, что в ряде случаев существенно упрощает их построение.
В общем случае, если система состоит из соединенных последовательно интегрирующих, апериодических, колебательных и форсирующих элементарных звеньев, то ее АФХ можно представить в виде
 , (4.40)
, (4.40)
По известным выражениям для ЛАХ типовых звеньев можно записать:
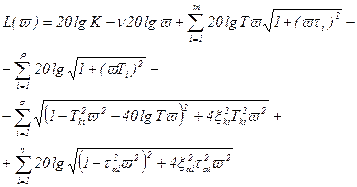 , (4.41)
, (4.41)
Это точное выражение ЛАХ разомкнутой системы. Однако, при построении обычно пользуются асимптотическими ЛАХ.
Для асимптотической ЛАХ можно записать выражение:
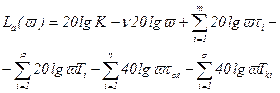 , (4.42)
, (4.42)
По известным выражениям для фазовых частотных характеристик типовых звеньев САР выражение для ФЧХ разомкнутой системы запишется следующим образом:
 ,
,
(4.43)
Анализ выражений (4.41) и (4.43) и асимптотических логарифмических амплитудных характеристик позволяет наметить следующий порядок построения ЛАХ.
1.Вычисляют частоты сопряжения по формулам:  и т.д. и наносят их на оси абсцисс.
и т.д. и наносят их на оси абсцисс.
2.Вычисляют значение 20lgK и откладывают его при частоте v=1.
3.Через эту ординату проводят низкочастотную часть характеристики (при v<v1) с наклоном -20×n дб/дек до первой сопрягающей частоты v1 (n - порядок астатизма системы, равный числу интегрирующих звеньев).
4.В точке v1 изменяют наклон характеристики в соответствии с тем, какому звену эта сопрягающая частота принадлежит, затем поступают таким же образом при частоте v и т.д.
Например, при апериодическом звене наклон изменяют на -20 дб/дек, при форсирующем звене первого порядка на +20 дб/дек и т.д.
5.Пользуясь кривыми для колебательных звеньев с соответствующими x, уточняют форму ЛАХ.
6.По формуле (4.43) строят логарифмическую фазовую частотную характеристику разомкнутой системы.
В качестве примера рассмотрим построение ЛАХ и ЛФХ последовательно соединенных звеньев, представляющих из себя тиристорный преобразователь (ТП), генератор (Г) и двигатель постоянного тока с независимым возбуждением. Рассмотрим данную систему при приложении управляющего воздействия (Uу(t)=0; Ic(t)=0). В этом случае передаточная функция двигателя примет вид
 , (4.44)
, (4.44)
где 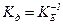 - передаточный коэффициент двигателя.
- передаточный коэффициент двигателя.
В результате получим структурную схему, представленную на рисунке 4.10, а.
Параметры системы заданы:
Kтп=40; Kг=10; Kд=1,2; Тг=0,5 с; Тп=0,01 с; Тэ=0,06 с; Тм=0,3 с.
Прежде чем приступить к построению характеристик, произведем некоторые упрощения. Из сопоставления электромагнитной постоянной времени якорной цепи Тэ и электромеханической постоянной Тм видим, что Тм>4Тэ, а это означает, что коэффициент демпфирования x>1 и двигатель может быть представлен двумя последовательно соединенными апериодическими звеньями с постоянными времени:
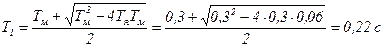 ,
,
(4.45)
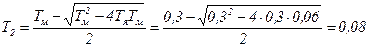 ,
,
(4.46)
Выделив пропорциональное звено с коэффициентом передачи  и учитывая (4.44), (4.44), (4.46), получим структурную схему, представленную на рисунке 4.10, б.
и учитывая (4.44), (4.44), (4.46), получим структурную схему, представленную на рисунке 4.10, б.
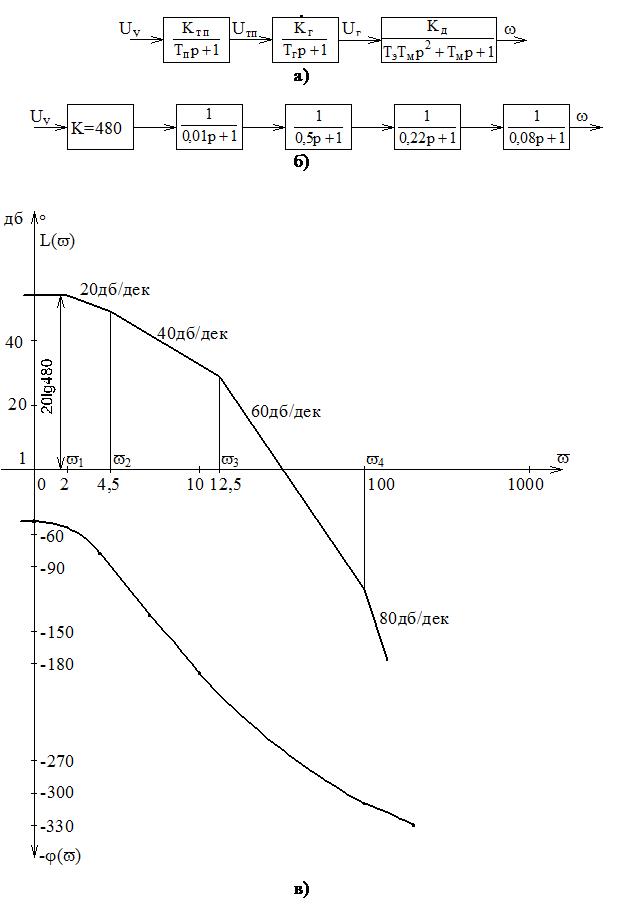
Рисунок 4.10 ЛАХ разомкнутой САУ
Вычислим сопрягающие частоты, начиная с той, которая соответствует наибольшей постоянной времени:
 , (4.47)
, (4.47)
Отмечаем сопрягающие частоты на оси частот (рисунок 4.10, в) и вычисляем ординату при частоте v=1. Она равна
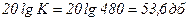 , (4.48)
, (4.48)
Через эту ординату на участке v<v1 проводим горизонтальную прямую, поскольку интегрирующие звенья в САР отсутствуют (n=0). При частоте v1=2 начнется участок наклонной ЛАХ с наклоном -20 дб/дек, так как сопрягающая частота соответствует апериодическому звену:
 . (4.49)
. (4.49)
При частоте v2=4,5 наклон ЛАХ увеличится еще на -20 дб/дек и составит -40 дб/дек. Такой наклон характеристики сохранится до частоты v3=12,5, при которой ЛАХ приобретет еще добавочный наклон -20 дб/дек, что соответствует апериодическому звену:
 , (4.50)
, (4.50)
И, наконец, наклон ЛАХ при частоте v4=100 увеличится еще на -20 дб/дек от действия апериодического звена
 , (4.51)
, (4.51)
Таким образом, начиная с частоты v4=100 ЛАХ имеет наклон -80 дб/дек.
Легко заметить, что ЛАХ (рисунок 4.10, в) могла бы быть также построена суммированием асимптотических ЛАХ отдельных звеньев: безинерционного (пропорционального) и четырех апериодических.
Построение ЛФХ (рисунок 4.10, в) произведено по формуле
 , (4.52)
, (4.52)
