Закон больших чисел в форме Чебышева

Случайной наз. величина в результате испытаний принимающая одно из мн-ва своих значений заранее не известное и зависящее от случайных величин, учесть, которые невозможно.

Последовательность СВ {ξn} сходится к СВ ξ по вероятности , если "e>0 limn→∞P{|ξn-ξ|³e}=0 или limn→∞P{|ξn-ξ|<e}=1

Говорят, что последовательность СВ {ξn} удовлетворяет закону больших чисел(ЗБЧ), если среднее значение этих СВ сходится по вероятности к среднему арифметическому их мат. ожиданий , т.е. "e>0 ;

Неравенство Чебышева. Для любой СВ ξ имеющей конечную дисперсию (Dξ<+∞) справедливо неравенство: P{|ξ-Mξ|≥e}≤Dξ/ 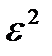, для " e>0

Теорема (ЗБЧ в форме Чебышева) Если последовательность независимых СВ ξ1, ξ2,…ξn имеет конечные мат. ожидания Мξi<+∞, i=1,n и дисперсии СВ ограничены одной и той же постоянной Дξi≤С, С=const, i=1,n то последовательность удовлетворяет ЗБЧ

Док-во: Покажем, что выполняется соотношение

Воспользуемся неравенством Чебышева: P{|ξ-Mξ|≥e}≤Дξ/ 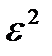, "e>0

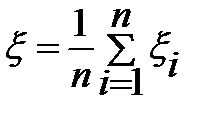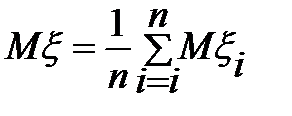Обозначим тогда , а 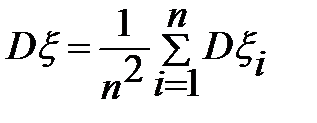(независимые СВ)

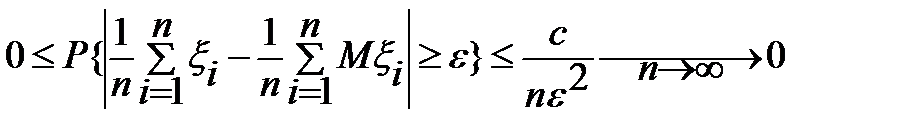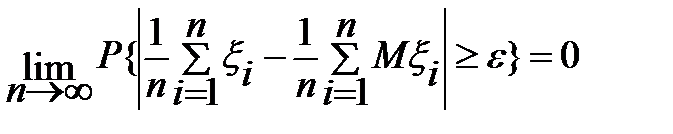=> ч.и т.д.

Эта теорема утверждает, что среднее арифметическое большого числа независимых СВ утрачивает характер СВ, т.е. сходится по вероятности к некоторому постоянному числу.

Теорема(необходимое и достаточное условие ЗБЧ) Пусть ξ1, ξ2,…ξn - последовательность произвольных СВ,для кот.выполн.след.соотношение

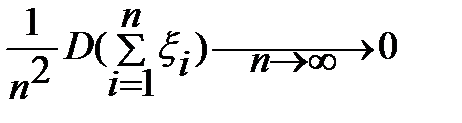, тогда рассм-я последовательность удовлетворяет ЗБЧ.

10.Формула полной вероятности. Теорема Байеса.Случайным наз.событие, кот.при выполнении некот.совокупности условий S может произойти или не произойти. Вероятность события А вычисл.в предположении,что нек.соб.B уже произошло наз.условной вероятностью события Аи обознач. .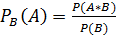

События А1…An образуют полную группу событий если выполняется: 1) хотя бы одно из событий обязательно происходит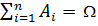

2) события попарно несовместны: т.е. , ,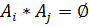

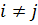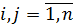
Теорема: Вероятность события В, которое может произойти только вместе с одним из событий А1…An, образующих полную группу событий,тогда вероятность события B определяется по формуле 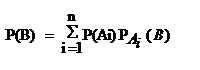док-во:Рассмотр.событие 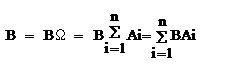, события ВA_i и BА_j несовместны т.к. 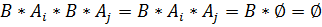, тогда получим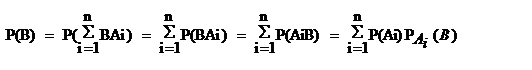

Теорема Байеса: Пусть событие В может произойти только вместе с одним из событий А1…An, образующих полную группу, тогда P(A_k) , вычисленная в предположении, что событие В уже произошло определяется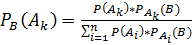

к=1,n. Док-воПо определению условной вероятности 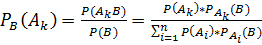ч.т.д.

11_Теорема о выборочной средней и выборочной дисперсиии.Опр.Выборочной совокупность. (выборкой) назюсовокупность случайно отобранных объектов.Опр.Генеральной совокупностью наз. совокупность объектов из которой производится выборка.Выборочные характеристики: 1)выборочной средней наз.характеристика вариационного ряда определ.по формуле 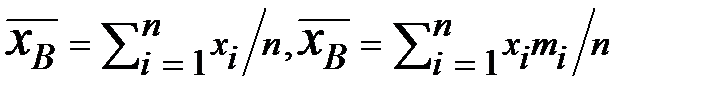. 2)Выборочной дисперсией наз.характеристика вариационного ряда опред.по формуле 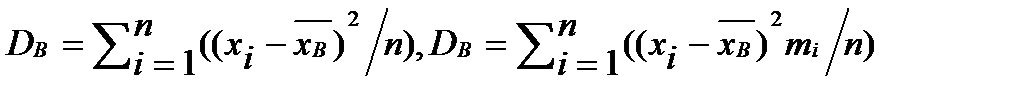Требования предъявляемые к статистическим оценкам: 1)q^*- несмещенная оценка:Мq^*=q.Если LimМq^* =q при n®¥,то оценка наз.ассимптотически несмещенной.Это требование означ,что по крайней мере в среднем оценка приводит к желаемому результату. 2)q^*-состоятельная оценка:.Иногда на практике проверяют достаточные условия состоятельности: а) LimMq^*=qпри n®¥; b)LimДq^*=0 при n®¥; с)q^*-эффективная оценка;Опр.Несмещенная оценка параметра q называется эффективной, если среди других несмещенных оценок этого параметра она имееет наименьшую дисперсию.Теорема (О выборочной средней).Выборочная средняя () вычисленная по n-независимым наблюдениям проведенные при одинаковых условиях над СВ Х,с MX=m;DX= 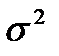является несмещенной и состоятельной оценкой математического ожидания и генеральной совокупности.Доказательство: 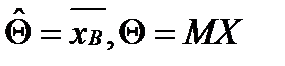1)Несмещенность: 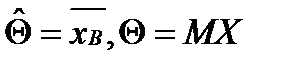, 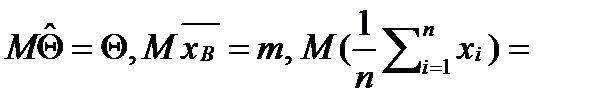[элементы выборки 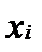явл.СВ,т.к.попадание в выборку случайно]= 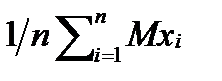=[т.к х_i независимые,одинакаво распределенные CD подчиненные тому же закону распредел.что и генерал.совокуп.X поэтому Мх_i=МХ;Дх_i=ДХ] =(1/n) 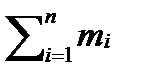=m. 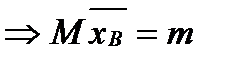. 2)Состоятельность: 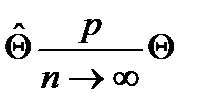,.Воспольземся нер-ом Чебышева P{|ξ-Mξ| ≤e}≥ 1-Дξ/e². ;;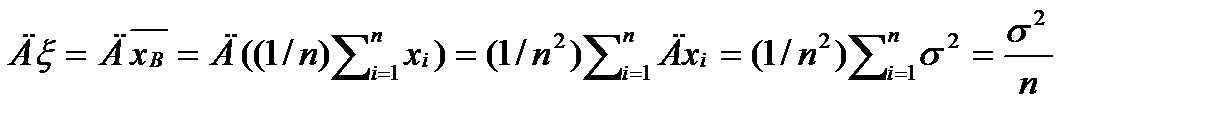

т.е.

Теорема (О выборочной дисперсии) Выборочная дисперсии (Д_в) вычисленная по n-независимым наблюдениям проведенных по одинаковым условиям над СВ Х с MX=m и ДХ=s² явл.смещенной оценкой дисперсии генеральной совокупности.

Доказательство. 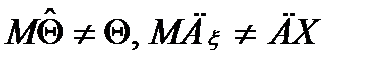.Преобразуем ;

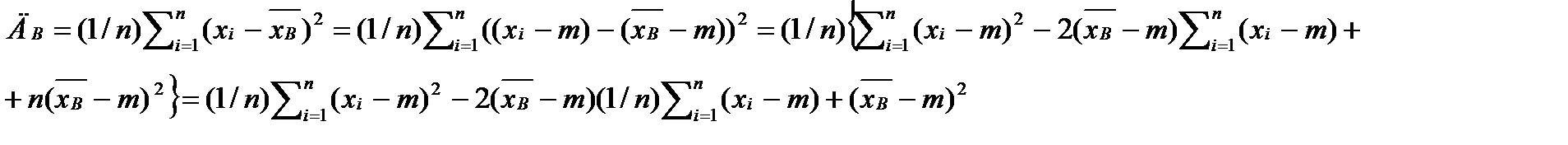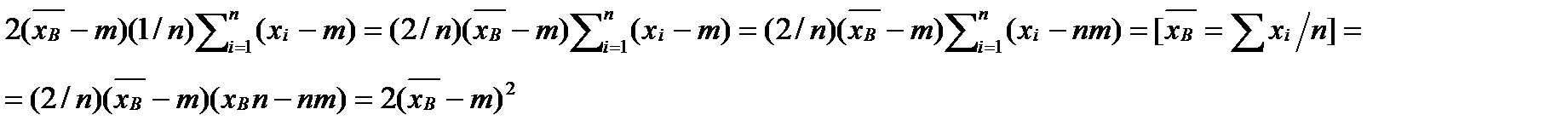
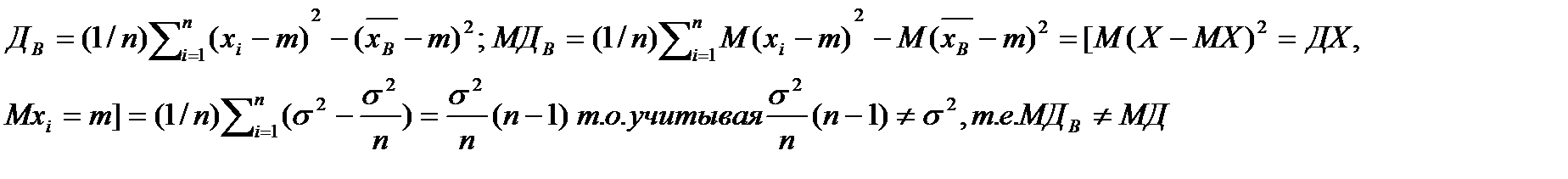
12_Основы программирования на языке Turbo Pascal.Типы данных в ТР делятся на 2 вида: Простые типы языка:Числовые (Byte, Short Int, Integer, Word, Long Int :Real, Логический Boolean, СимвольныйChar, Строковый String, , Адресный тип Pointer позволяет работать с адресами памяти; Составные типы языка. Компоненты величин данного типа строятся на базе других типов (Array ,Record Файловый Объектный тип Object. Позволяет помимо задания собственного типа, определить круг операций, применимых к экземплярам данного типа).Массивэто упорядоченная по размещению конечная пос-ть эл-ов одного и того же типа. Описание Array [диапазон] of Тип Элементов, где Диапазон – опис диапазона изменения индексов; Тип элементов – базов тип эл-ов данного массива. Пр. Var a : Array[1..20] of Integer – вектор элементов целого типа; b : Array[1..20, 1..10] of Real матрица 20х10 эл-тов вещественного типа.; Обращение к элементу: a[1] – к 1-му эл-ту;

Запись. Назначение записного типа состоит в компактном представлении данных разного типа. Это единственный тип данных, компоненты которого м.б. разного типа. Компонент записи наз. поле. Типы полей могут быть практически любыми. Записи наиболее естественным образом могут отразить характеристики моделируемых реальных объектов. Описание: Record поле1 : тип1; …полеk : типk; end; Пр. Type RecType = Record x,y : real; end; Var Point : RecType; Т.е. описана переменная, задающая декартовы координаты. Помимо простого оформления записного типа разрешается использовать записной тип с вариантной частью, при чем вариантная часть м.б. оформлена 2 способами (вариантная часть с сигнальным значением, способ «по контексту»). Цель введения вариантной части: добиться возможности определения нескольких структур в рамках 1-ого типа. Место расположения вариантной части после перечисления фиксированных полей записи. Для обращения к полю необходимо: ИмяПеременной.ИмяПоля;Пр. Point.x – обращение к полю x переменной Point. Поскольку при работе с записями постоянно приходится указывать имя переменной с точкой, то используют оператор присоединения with. With Имя Записной Переменной Do Оператор; Пр. With Point Do Begin x := 10; y := y+5; end; Символы и строки. ТР поддерживает стандартный символьный тип Char. Строковый тип данных String толкуется как вектор элементов типа Char. Задание эл-тов: символ алфавита, взятый в апострофах ‘A’; задание кодом ASCII: #32=’ ‘ – пробел; Var s : string; - описана строка длиной до 255 символов; S20 : string[20]; - описана строка длиной 80 символов. s:=’Строка сомволов’; s[1] = ‘С’; Длина строки <=255 символов. Функции для работы с символами и строками: Chr(x:byte):char – по коду возвращает символ. Ord (x: char): byte – по символу код. Pred(C:char):char символ предшествующий данного; Succ(C:char):char следующий; UpCase(C:char):char малую букву в большую; Length(s : string) : byte – определяет длину строковой величины. Ссылки. Динамизм структуры переменных может проявл-ся в том, что захват места под динамические структуры и величины и их освобождение осущ-ся по мере необходимости. Они исп-ся когда: переменные имеют большие размеры, но вместе с тем они нужны в одном участке программы, а в другом нет; при работе нужен массив или др. структура, размеры которой трудно предсказуемы; когда размер переменной больше 64К. Основной механизм задания динамических данных таков: выделение непрерывного участка памяти ОЗУ соотв-их размеров в спец. области – куче; сохранение адреса начала этого участка в спец. переменной, кот. наз. ссылочной. Описание: Type Имя ссылочного типа = ^ИмяБазовогоТипа; Пр. Type IntPtr = ^Integer; Var j : IntPtr; - описана переменная j ссылочного типа на целочисленное значение.

Во множестве ссылок определена операция инициализации или заниливания. j := nil; Она содержит адрес начала участка, в кот. размещается значение динамической переменной. Для того чтобы извлечь это значение служит операция разименования. Суть этой операции закл. В переходе от адреса к значению, хранащемуся по этому адресу. Описание: ИмяСсылочнойПеременной^ Пр. j^ это значение, которое хранится по адресу, на который указывает переменная j. Перед началом работы с динамической переменной необходимо захватить место для нее в области кучи. New( Var P : Pointer) – размещение динамической переменной; GetMem( Var P : Pointer; Size : word) – захват в области кучи неразрывного блока памяти размером Size. New (Имя Типа Ссылки) : Pointer; Для освобождения памяти из-под динамических переменных служат процедуры: Dispose (Var P:Pointer) – освобождает память, отведенную под значение p^ процедурой New. FreeMem (Var P:Pointer; Size : Word) – освобождает непрерывный участок памяти размером Size, на который указывает указатель P.

Для управления состоянием кучи служат процедуры: Mark(Var P : Pointer) – запоминает в переменной P тек. состояние кучи. Release (Var P:Pointer) – возвращение кучи в состояние, запомненное в указателе P процедурой Mark. MaxAvail : LongInt – определяет суммарную свободную память в области кучи.

13. Основы программирования на языке Pascal.Основными языковыми структурами управления процессом обр-ки инф-ии явл-ся операторы. Оператор программы – это единое неделимое предложение языка программирования, приводящее к выполнению действия. Простые операторы: 1) := присваивание; 2) вызов процедуры; 3)оператор безусловного перехода GoTo; 4)пустой оператор; Один оператор от другого отделяется “;”.Составной оператор – это последовательность операторов, перед которой стоит ключевое слово begin, а в конце end. Begin..End наз. операторными скобками. Там, где стоит простой оператор, может стоять и составной.Условный р:If Условие Then Оператор1 Else Оператор2Цикл с предусловием: While Условие Do Оператор Цикл с постусловием:Repeat Оператор Until Условие;Цикл с параметром: For Управл. Переменная := исх. Значение To/DownTo Конечное значение Do Оператор; Описание процедур и функций: Procedure Имя (список формальных параметров); раздел описаний; begin оператор; end; Function Имя (список формальных параметров): имя типа; раздел описаний; begin оператор; end; Вызов процедуры: ИмяПроцедуры Формальные параметры явл. локальными переменными и используются для связи между вызываемой и вызывающей прогр-ми. Формальные параметры делятся на 2 вида: параметры-значения и параметры-переменные. Параметры-значения это локальные переменные, значения кот. передаются из вызывающей прогр-мы. Могут изменятся в теле подпрогр-мы. Параметры-переменные – когда значения могут передаваться из и в вызывающую программу. Эти параметры изменяются в теле подпр-мы. Через эти параметры разрешен доступ к участку памяти, в кот. размещены знач-я всех величин головной прогр-мы. Измененные знач-я параметров переменных сохр. при выходе из подпрогр-мы. В связи с этим фактические параметры переменных должны быть только идентификаторами переменных. Особый случай – подпрогр-мы-ф-ии. Вычисленное знач-е передается в прогр-у через идентификатор подпрограммы ф-ии. По этой причине в теле подпр-мы-ф-ии ее идентификатору должно быть присвоено знач-е. Вместе с тем подпр-ма-ф-я может им. параметры переменные, через кот. можно получать просчитанные в ней значения. Модуль в ТurboРascal – это спец. образом оформленная библиотека определений: типов данных, констант, переменных, процедур и ф-й. Модуль не может быть запущен на вып. самостоятельно. Он лишь участвует в работе др. прог-м. Модуль должен быть предварительно откомпилирован и рез-т - tpu-файл - должен быть сохранен на диск. Для исп. этого файла его имя должен быть подключено к основной прогр-е директивой Uses Имя1, Имя2.Синтаксис: 1)Unit имя модуля;2) Interface {начало раздела объявлений}Uses Mod1, Mod2…;Const {блок библиотечных констант}Type{ блок библиотечных типов}Var{ блок библиотечных переменных}{заголовки процедур и функций}3) implementation {начало раздела реализаций}Uses Mod11, Mod12…;Const {блок внутренних констант}Type { блок внутренних типов}Var { блок внутренних переменных}Label {блок описания меток блока инициализации}{реализация объявлений процедур и ф-й}4) begin {блок инициализации}end.1) Заголовок – вводит имя модуля по которому он будет подключаться к другим подпрограммам и модулям. Имя должно быть уникальным и должно совпадать с именем исх. текста данного модуля. 2) Содержит описание библиотечных типов, констант, переменных, кот. могут использоваться в вызывающиш программах. 3) Содержит тела процедур и функций. Можно объявлять типы, переменные и константы. Все они будут глобальными для подпрограмм модуля. 4) То что должно быть выполнено перед выполнением основной программы.

14_Элементы ООП.Исторически первой идеей, лежащей в основе языков программирования, была идея процедурного структурирования (язык Фортран). Результат этого этапа – создание обширных библиотек, т.е. своеобразного стройматериала, на основе кот. можно было решить достаточно сложные технические или матем. задачи. Прогресс в области вычислительной математики привел к тому, что основной акцент в программировании стали делать на организацию данных и программный контроль за правильностью использования этих данных на этапе компиляции и на этапе эксплуатации (Pascal, C).Начиная с языка Симула-67 начался новый этап технологии программирования – а именно этап объектно-ориентированного программирования (ООП). Основная идея этого этапа – установление связи в данных и объединение их с процедурами их обработки в единый объект.Характерные черты объекта:Инкапсуляция— это механизм программирования, который связывает код (действия) и данные, которыми он манипулирует, и при этом предохраняет их от вмешательства извне и неправильного использования.Наследование — это процесс, благодаря которому один объект может приобретать свойства другого. Благодаря наследованию поддерживается концепция иерархической классификации.Любой наследник наследует описание данных прародителя и доступ к их методам обработки.Эти обстоятельства находят отражение в синтаксисе объекта наследника: Type Имя_Обекта_Наследника = Object (Имя_Объекта_Прародителя) Новые поля объекта наследника; Новые Методы Объекта Наследника; End;Полиморфизм. Суть состоит в возможности присваивания определенному методу одного имени, используемого совместно во всей иерархии объектов снизу доверху. При этом каждый объект иерархии будет реализовывать соотв-ий метод в соответствии с тем определением, кот. было сделано в соответствующем ему объектном типе либо в ближайшем по нисходящей объектном типе прародителей.

Однако это свойство работает не совсем корректно при использовании статических методов. В этом случае будет вызываться метод прародителя. Дело в том, что особенностью статич. методов явл. свойство раннего связывания. Суть: установление связи между объектом и методом на этапе компиляции программы. В этом смысле обработка статич. методов похожа на обр-ку статических переменных. Т.О. если метод прародителя вызывает другие методы (методы потомка) в случае использования статических методов, то последние тоже будут методами прародителя. Сво-во полиморфизма объектов и реализуется за счет виртуальных методов. Синтаксис: Procedure ИмяМетода (Параметры;); Virtual; Function ИмяМетода(Параметры;): тип значения; Virtual; Если прародительский тип описывает некоторый метод как виртуальный, то все производные типы, реализующие метод с тем же именем, д.б. виртуальными. В описании объектного типа описывается спец. метод инициализации обекта, как метод с идентификатором Init. Причем заголовок оформляется по-особому. Вместо Procedure надо использовать Constructor. Его следует вызывать до первого вызова виртуального метода. Имя_Ссылки_На_Объект^.ИмяПоля – обращение к конкретному полю объекта;Имя_Ссылки_На_Объект^.Метод – вызов метода конкретного экземпляра объекта. Создание динамического экземпляра объекта производится процедурой New(ИмяСсылки НаОбъект) – выделение в области кучи участка для хранения экземпляра объекта. Для виртуальных методов используется расширенная процедура New(ИмяСсылкиНаОбъект, ИмяКонструктора(Параметры)); Эта процедура выделяет участок памяти под объект и выполняет вызов конструктора.

Для освобождения памяти из-под динамических экземпляров объекта происходит процедурой Dispose(ИмяСсылкиНаОбъект); Однако эта процедура уничтожает весь объект в целом. Это означает, что если сам объект имел динамические поля, то при освобождении объекта эти поля должны освобождаться раньше, чем сам объект. Для подобных целей вводится метод с названием Destructor. Этот метод противоположен конструктору. Деструкторы м.б. как статичными так и виртуальными. В этом случае освобождение объектов происходит так: Dispose (Имя_Ссылки_На_Объект, Имя Деструктора).

15_Абстрактные типы (структуры) данныхОснов структур данных, присущими всем языкам програм явл-ся вектор и матрица называемые обобщенно таблица и массив. До недавнего времени програм реальных процессов сводилось к умению моделировать реальную инф-ю с пом. только этих структур. В связи с этим пришли к целесообразности структуриров не только текста алгоритмов, но инф-и, т.е. данные. Благодаря этому в практике програм-я закрепились след. структуры данных (СД): Стек; Очередь; Дек; Множество; Последовательность;; Динамический вектор; Бинарное дерево, Дерево общего вида.Стек – это динамическая СД элементов одного и того же типа Е, доступ к которым организован по правилу «последним пришел, первым вышел». Основ операции: S. в стек(арг эл:E)/ из стека(рез эл:E)/стек пуст:лог/есть своб место: лог/, Очередь - это динамическая СД элементов одного и того же типа Е, доступ к которым организован по правилу «первым пришел, первым вышел».Дек – это динамическая СД элементов одного и того же типа Е с двумя равнодоступными по обеим операциям (чтение-запись) концами. Дек это двусторонняя очередь.Среди принципов построения данных СД выделяют: -построение СД на базе вектора; -построение СД на базе связного списка. Вектор как СД встречается практически во всех языках прогр-ия. Поэтому возникает мысль об исп. данной структуры как основы для построения данных СД. Кроме того все его эл-ты одного типа, как и у данных СД. Вопрос об исп. вектора в качестве базы реша-ся след. образом: выбирается вектор размерности n элементов типа Е; помимо этого для моделирования структур требуется вводить 1 или несколько вспомогательных величин (переменных), в зависимости от сложности структуры. В частности в случае моделирования стека достаточно одной вспомогательной величины, кот. можно назв. вершина. В случае очереди 2 величины: начало и конец. Совокупность средств: вектор-носитель и вспомогательные величины позволяют моделировать работу всех рассматриваемых выше СД. Недостатком данной реализации явл. несоотв. между свойством динамичности моделируемых структур и статичностью базового носителя вектор. Этого недостатка лишена структура связный список. Элементы вектора неявно упорядочены (за счет индексов). Исп. связный список данное свойство придется реализовывать явно, за счет дополнительного указания в узле структуры адреса очередного элемента. Структура узла связного списка будет такой: Содержание Адрес Адрес предназначен для хранения адреса очередного элементам Однако связный список имеет недостаток: он требует большего объема памяти, чем вектор. Поэтому структура «связный список на базе вектора» явл. своеобразным компромиссом между первыми двумя. В общем случае связный список им. 2 поля: поле для хранения инф-и и поле для хранения адреса.Бинарное дерево (БД) – это динамическая СД эл-ов одного и того же типа Е, представляющих мн-во, которое либо пусто (случай пустого БД), либо содержит один элемент, называемый корнем БД, а все остальные делятся на 2 взаимно непересекающихся п/множества. Одно из кот. наз. левым поддеревом, а др. правым поддеревом данного БД. Каждое из них представляет собой БД. Эл-ты деревьев наз. узлами.(нарисовать дерево) Дерево,реализуетсяпрежде всего на динамич структурах, т.е. узел дерева содержит два поля-ссылки – на левое и правое поддерево для двоичного дерева и на брата и старшего сына для дерева общего вида. Дерево уже не явля. линейной структурой, поэтому представление деревьев на последовательной памяти (файлах) представляет собой определенную проблему. Однако все данные хранятся во внешней памяти в виде файлов, поэтому реш-е этой проблемы необходимо. Тем не менее, сразу стоит оговориться, что это представление не будет в полной мере реализацией АТД дерева на структуре данных файл, поскольку требуется лишь создать обратимое отображение дерева в файл – никаких операций с файлом-деревом совершаться не будет. Создадим новый тип узла дерева– запись информационного поля и поля, хранящего число поддеревьев данного узла. В файл будем последов. записывать каждый узел так, чтобы поддеревья записывались после своего корня. Обратная операция производится с исп. рекурсии. Читаем из файла узел дерева, создаем его и ссылки на его поддеревья. Затем для всех указанных поддеревьев повторяем ту же процедуру.

16.Основы концепции ООП. Реализ-я принципов ООП в выбранном языке прог-ия.ООП - методология программ-я, основанная на представлении прог-мы в виде совокупности объектов, каждый из кот. явл. реализацией определенного типа, использующая механизм пересылки сообщений и классы, организованные в иерархию наследования. Принципы:Инкапсуляция— это св-во сис-мы, позволяющее объединить данные и методы, работающие с ними, в классе и скрыть детали реализации от пользователя(классич. правило ООП утверждает, что для обеспечения надежности нежелателен прямой доступ к полям объекта: чтение и обновление их содержимого должно производиться посредством вызова соотв. методов). Наследование— это св-во сис-мы, позволяющее описать новый класс на основе уже существующего с частично или полностью заимствующейся функциональностью(этот принцип означает, что если вы хотите создать новый класс, лишь немного отличающийся от старого, то совершенно нет необходимости в переписывании заново уже существующих полей и методов). Класс, члены которого наследуются, называется базовым классом, а класс, который наследует эти члены, называется производным классом. Полиморфизм— это св-во сис-мы исп. объекты с одинаковым интерфейсом без инф-ции о типе и внутренней структуре объекта(или это возможность взаимодействия с объектом, не зная, к какому конкретному классу он относится). Объект(экземпляр класса)- это модель или абстракция реальной сущности в программной сис-ме. Объект лежит в основе методологии ООП. Класс — это шаблон, кот. определяет форму объекта. Определяя класс, мы опред. данные, кот. он содержит, и код, манипулирующий этими данными. У класса есть имя(идентификатор), атрибуты(описывают св-ва его объектов) и методы(описывают его поведение). Интерфейс — это внешняя часть класса. Интерфейсопределяет набор методов, которые будут реализованы классом. Сам интерфейс не реализует методы. Можно сказать, интерфейс представляет собой контракт, в кот. класс, реализующий интерфейс, должен реализовывать каждый аспект этого интерфейса в точном соотв. с его определением. Ф-ии(ф-ии-члены) и переменные(данные-члены), объявленные внутри класса, становятся членами этого класса. А именно, к ним относят поля (св-ва) и методы/ф-ии/процедуры. В зав. от языка програм-я к этому списку могут добавиться константы, атрибуты и внешние определения. Классы могут задавать поля- то есть переменные, принадлежащие либо непосредственно самому классу (статические), либо экземплярам класса (обычные). Статические поля существуют в одном экземпляре на всю прог-му. Обычные поля создаются по одной копии для каждого конкретного объекта — экземпляра класса. (Напр., общее кол-во строк текста, созданных в прогр-ме за время её работы, будет явл. статическим полем класса «строка текста». А конкретный массив символов строки будет явл. обычным полем экземпляра класса «строка текста»). Как и поля, код в виде методов/фу-ий/процедур, принадлежащих классу, может быть отнесен либо к самому классу, либо к экземплярам класса. Метод, принадлежащий классу и соотнесенный с классом (статический метод) может быть вызван сам по себе и имеет доступ к статическим переменным класса. Метод, соотнесенный с экземпляром класса (обычный метод), может быть вызван только у самого объекта, и им. доступ как к статическим полям класса, так и к обычным полям конкретного объекта( Напр., общее количество созданных строк можно узнать из любого места программы, но длину конкретной строки можно узнать только указав, тем или иным образом, длину какой строки будем мерить). Рассм. C#. Создание класса:

class имя_класса { Пр.class Building {// класс «здание»

// Объявление переменных экземпляров. public int floors; // кол-во этажей

доступ тип переменная1; public int area; //площадь здания

. . . }

доступ тип переменная N;

// Объявление методов.

доступ тип_возврата метод 1 (параметры) {// тело метода}……

доступ тип_возврата метод N {параметры) {// тело метода} }

доступ: private -данные-члены и ф-ии-члены доступны только для ф-ий-членов этого класса; protected -данные-члены и ф-ии-члены доступны для ф-ий-членов данного класса и классов, производных от него; public -данные-члены и ф-ии-члены класса доступны для ф-ий-членов этого класса и др. ф-ий проги, в кот.им. представитель класса. Описанный пример-пример создания базового класса.

Создание объекта: имя_класса имя_объекта = new имя_класса(); Пр. Building house = new Building(). В рез. переменная house будет ссылаться на объект типаBuilding.Оператор new динамически выд. памятьдля объекта и возвращает ссылку на него.

Производный класс. Общая форма объявления класса, кот. наследует базовый класс, им. такой вид: class имя__производного_класса : имя_базового_класса { // тело класса}

Пр. class TwoDShape{<общие м-ды>} //класс двумерных объектов – базовый класс

class Triangle : TwoDShape{<общие м-ды> + <свои м-ды>} // класс треугольников – производный класс. Для создаваемого производного класса можно указать только один базовый класс. В С# (в отличие от C++) не поддерживается наследование неск-их базовых классов в одном производном классе. Однако можно создать иерархию наследования, в кот. один производный класс становится базовым для другого производного класса.

В С# 2 или больше методов внутри одного класса могут им.одинаковое имя, но при усл-ии, что их параметры будут различными. Такую ситуацию наз. перегрузкой методов, а методы, кот. в ней задействованы,-перегруженными. Все перегруженные методы должны иметь списки параметров, кот. отличаются по типу и/или кол-ву. При вызове перегруженного метода вып-ся та его версия, параметры кот. совпадают (по типу и количеству) с заданными аргументами. Посредством перегрузки методов в С# поддерживается полиморфизм.

Пр. class Overload { public void ovlDemo() {}

public void ovlDemo(int a){} // Перегружаем метод ovlDemo() для одного целочисленного параметра

public double ovlDemo(double a, double b){} // Перегружаем метод ovlDemo() для 2-х double-параметров }

Виртуальнымназ. метод, объявляемый с помощью ключевого слова virtual в базовом классе и переопределяемый в одном или нескольких производных классах. Т.о., каждый производный класс может иметь собственную версию виртуального метода. Чтобы объявить метод в базовом классе виртуальным, его объявление необходимо предварить ключевым словом virtual . При переопределении виртуального метода в производном классе используется модификатор override.При переопределении метода сигнатуры типа у виртуального и у метода-заменителя должны совпадать. Виртуальный метод переопределять необязательно. Если производный класс не предоставляет собственную версию виртуального метода, исп. версия, определенная в базовом классе.Если производный класс не переопределяет виртуальный метод в случае многоуровневой иерархии, то будет вып. первый переопределенный метод, кот. обнаружится при просмотре иерархической лестницы в направлении снизу вверх. Кроме того, виртуальный метод нельзя определять как статический (с использованием слова static ) или абстрактный (с использованием словa abstract).

Пр. class Basa { public virtual void who () {}} // Создаем виртуальный метод в базовом классе,

class Derivedl : Basa { public override void who() {}} // переопред. метод who() в производном классе,

class Derived2 : Basa {public override void who() { }} //переопред метод who() в др.производном классе

Cредством, благодаря кот. производный класс переопределяет все необх. методы, в С# явл. абстрактный метод. Абстрактный метод создается с помощью модификатора типа abstract. Абстрактный метод не содержит тела и, следовательно, не реализуется базовым классом. Поэтому производный класс должен его переопределить, поскольку он не может использовать версию, предложенную в базовом классе. Абстрактный метод автоматически является виртуальным. Формат записи: abstract тип имя(список_параметров); Модификатор abstract можно использовать только применительно к обычным, а не к static-методам. Св-ва также могут быть абстрактными. Класс, содержащий один или несколько абстрактных методов, также должен быть объявлен как абстрактный с помощью спецификатора abstract, кот. ставится перед объявлением class . Поскольку абстрактный класс нереализуем в полном объеме, невозможно создать его экземпляры, или объекты. Т.о., попытка создать объект абстрактного класса с помощью оператора new приведет к возникновению ошибки времени компиляции. Если производный класс выводится из абстрактного, он может реализовать все абстрактные методы базового класса.

Интерфейсы объявляются с помощью ключевого слова interface.

17_Предел числовой последовательности и его свойства. Критерий Коши и Вейерштрасса существования предела. Число е. Опр.числовой последовательностью наз.f отображ. 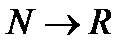,т.е.фун-ия определенная на мн-ве натурал.чисел значение 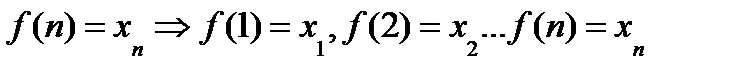и т.д. 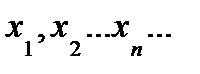- члены числовой последовательности.Обознач: 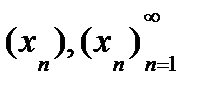.Опр.число А явл.пределом последов. 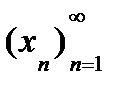если какова бы ни была 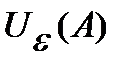найдется такой ,что все члены последов.с индексами большими чем 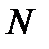попадают в 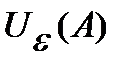, 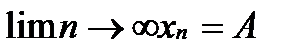.Опр.Будем говорить,что последовательность xkсходится к точке x из R, если 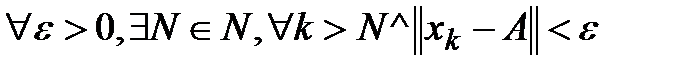. При этом x называется пределом последовательности xk. Обозначение: lim xk=x или xk->x при k 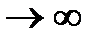.Последовательность назовем расходящейся, если она не сходится ни к одному действительному числу.

Критерий Вейерштрасса: Неубывающая последовательность имеет предел <=> когда эта последовательность ограничена сверху.Док-во:Необх: дано 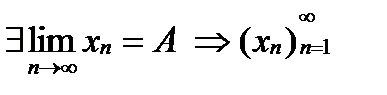‑ ограничена и 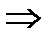по теореме x_k – неубывающая огран последоват.Дост:дано 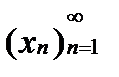‑ неубывающая, x_n–ограничена сверху док-во из данного 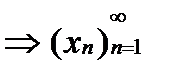имеет точную верхнюю грань т.е. 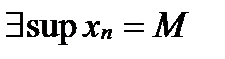(по св-ву точных граней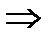

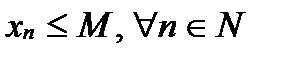
1) 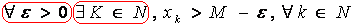в силу того что послед неубыв будем иметь, что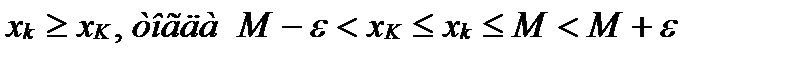

2) 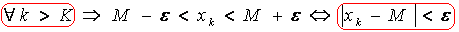Из выдел 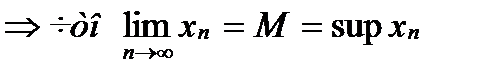Теорема доказана.

Опр.Последов. 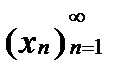наз.фундаментальной,если для 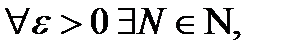такой что для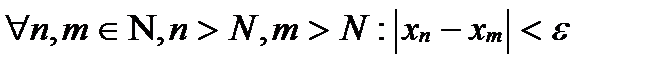

Теорема (критерий Коши существования предела). Последовательность имеет предел <=> когда она фундаментальна.Т.:Всякая невозраст. И огранич.снизу последов.им.предел причем этот предел совпадает с нижней гранью мн-ва элементов данной последовательности. .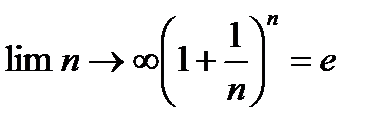

18. Предел и непрерывность функции в точке. Основные свойства предела функции. Локальные и глобальные свойства непрерывных функций. Опр(по Гейне) Число А предел ф-ии f(x): если какую бы последов-ть значений аргументов стремящихся к точке х₀ не извлечь (причем члены пос-ти различны и отличны от х₀₎, то соответственно последовательность значений ф-ии стремится к числу А. 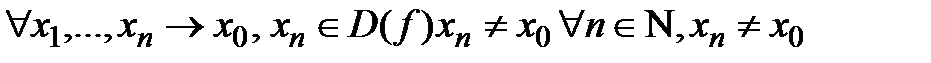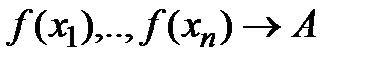. Опр(по Коши): Число А наз-ся пределом ф-ии f(x) если для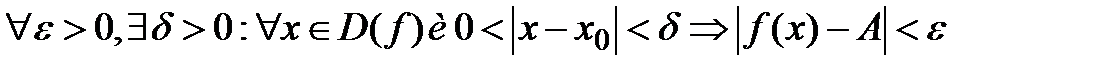 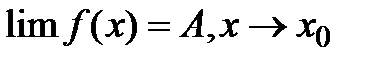. Т. Опр-я предела по Коши и по Гейне эквивалентныОбщие св-ва предела ф-ии: Т1. (О единственности предела)Функция f(x) при х->а может иметь не более одного предела. Т2. (О предельном переходе в нер-вах) Если 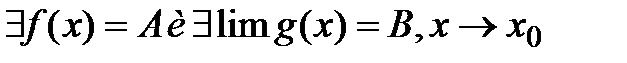причем А<B, то справедливо f(x)<g(x). Т3 (О пределе зажатой ф-ии) Пусть для 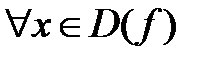выполняется 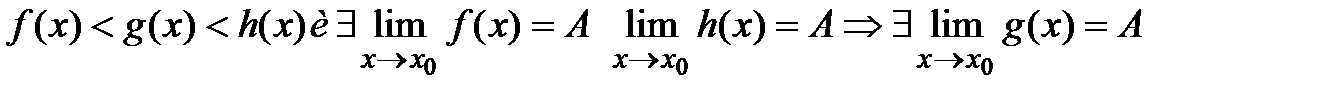. Т4 (О сохранении ф-ей знака предела) Пусть 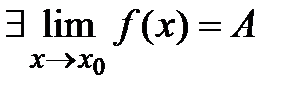. Если А<0, то 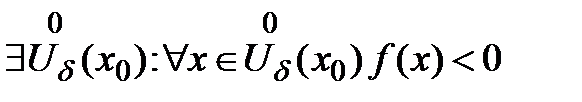(следствие Т2)Опр ф-ия 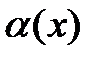наз-ся бескон малой если 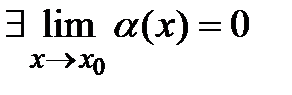. Т(О сущест конечного предела ф-ии) 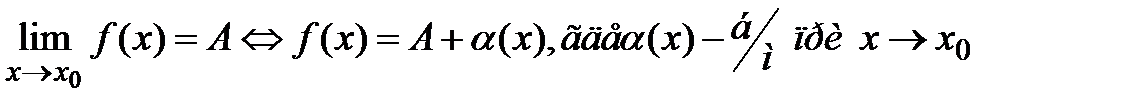. 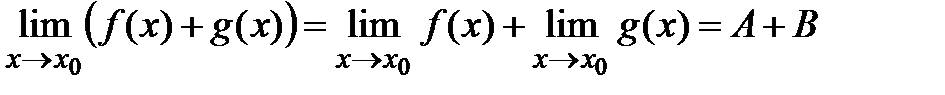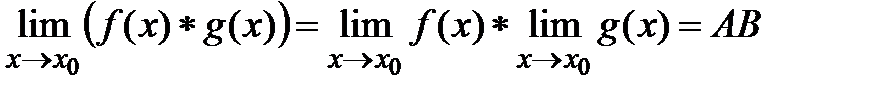Т(О перделе суммы, произв, частного) Если f и g имеют конеч пределы, то , , 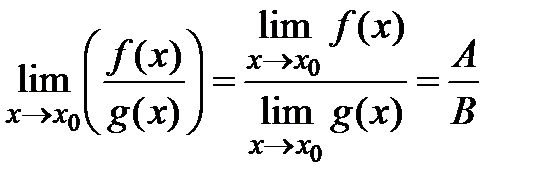если В 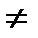0..Т(Кр Коши) 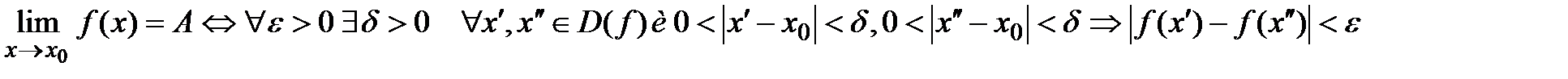1-ый зам. предел: 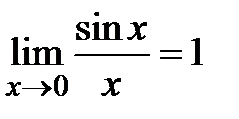;2-й зам. предел: 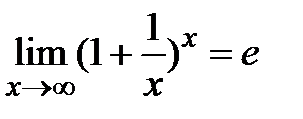.Опр. Ф-я y=f(x) наз-ся непр. в т. 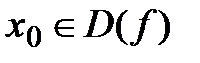если 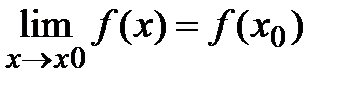. Опр точка х явл точкой разрыва если вып-ся одно из усл: 1. 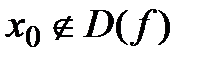2. не существ 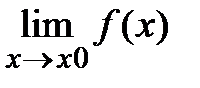3. 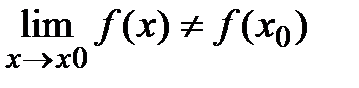. Разрыв I-го рода:в т. х=а ф-я f(x) имеет конечные односторон пределы. Разрыв II-го рода: если хотя бы один из односторон пределов явл. бесконечным. Т1(Св-ва) Если ф-ии f(x) и g(x) непрерывны в некоторой обл 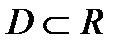то f(x)+g(x);f(x)*g(x); f(x)/g(x) - непрер на пром-ке если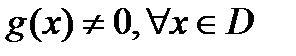

Локальные св-ва непрерывных ф-ий: Т.если ф-я y=f(x) непр-на в т. х0, то она огр-на в нек-й окр-ти этой точки.Т. если f(x0)>0 и f непр-на в т. х0, то сущ-ет окр-ть U(x0), что f(x)>0. Глобальные св-ва: Т1. Больцана-Коши: если f(x) непр-на на [a,b], на концах отрезка принимает зн-я разных знаков f(a)f(b)<0, то сущ-ет C принад [а,b], такое что f(c)=0. Т.Вейерштрасса: если ф-я непрерывна на [a,b], то она на нем ограничена. Т.е. 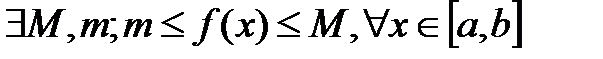Док-во(от противного):Путь f не ограничена, то 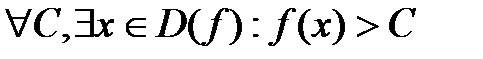. В качестве С выберем: 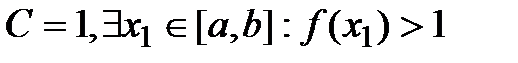… 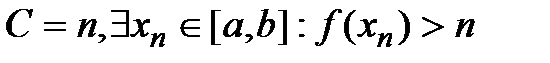, т.е выделели пос-ть х₁…х_n- ограничена, т.к а<х_n<b-> по теореме Б-В существ подпосл 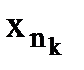-> C Т.к f непрерывна в точке х=С, т.е 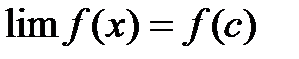при х->С След-во 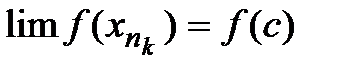, т.е конечен. А это противоречит тому что f(х_n)>n Предполож неверно -> f ограничена сверху. чтд Т.2-я Вейерштрасса: непр-на => достигает своего наим. и наиб. значения.(т.е. точных граней) т.е. 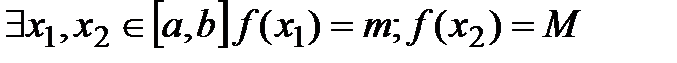. Т.Кантора: Если ф-я непр-на на отрезке, то она равномерно непр-на на нем

19. Производная и дифференциал. Основные теоремы дифференциального исчисления, формула Тейлора. Условия монотонности, выпуклости и локального экстремума функции. Опр Пусть ф-я y=f(x) непрерыв.в некот.окресности U(x0) 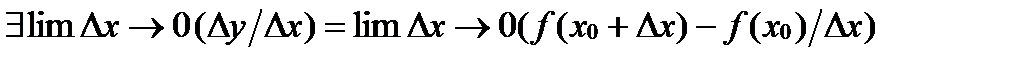(предел разностного отн-я 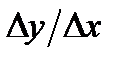)и он конечен,то эту величину наз.производной фун-ей в т.x0 и обознач.: 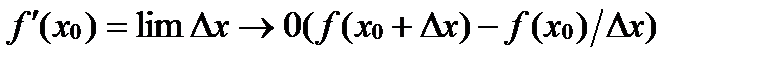.Опр. y=f(x) наз. диф-мой в т. х0,если приращение 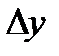в т.х0 соотв-щее приращению 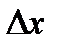аргумента, м.б. представлено в виде: 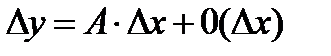. Т.Ферма:Если ф-ия f(x) принимает во внутренней точке 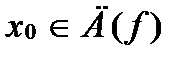наибол.или наим.знаач,то если сущ.производ. 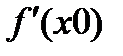,то она =0.Т.Ролля: Пусть y=f(x) определ.и непр-на на [a,b],им.в каждой т-ке (а,b) производную,и f(a)=f(b),тогда найдется такая т-ка 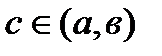,что 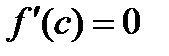. Т.Лагранжа: Пусть y=f(x) определ.и непр-на на [a,b],диф-ма во всех внутр.точках [a,b],тогда найдется такая т.с 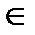(а,b),что для нее спр-во 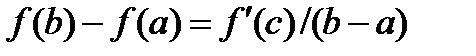, 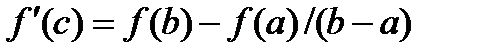.Док-во:введем вспомогательную ф-ию 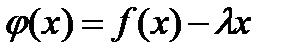.Подберем 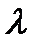таким образом,чтобы ф-ия 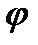удовлетвор.теор.Ролля: 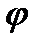-непрерыв.на[a,b], 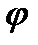-диференц.на (a,b), 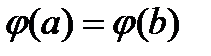. 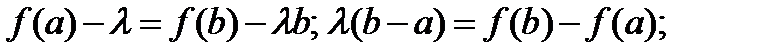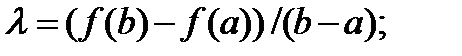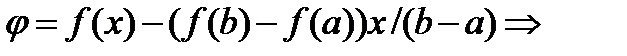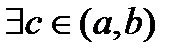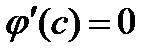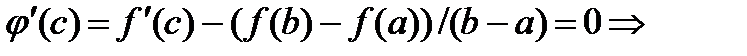(по теор.Ролля) такая что , 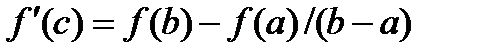Т.Коши: Пусть ф-и f(x) и g(x) опред.и непр-ны на [a,b],диф-мы на (a,b),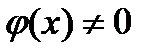 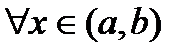,тогда 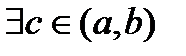такая,что выполняется .

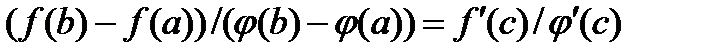Ф-ла Тейлора: 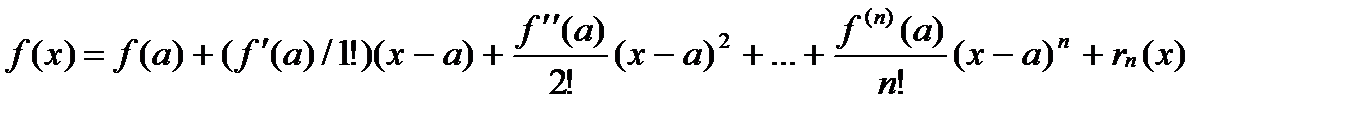, 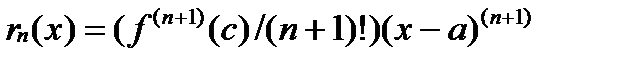-ост.член. Усл-е монотонности:f(x) определ.и диф-ма на (a,b) => эта ф-я строго монотонно возр. на (a,b), если 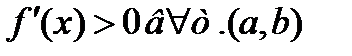, и строго монотонно убывает, если 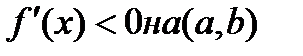. Теорема Ферма выраж.необход.условие локального экстремума: чтобы т-ка 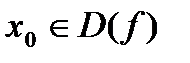была т-кой экстремума необх.чтобы выполнялись усл-я . Усл-е выпуклости ф-ии:y=f(x) на (a,b) имеет 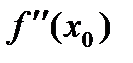конеч. и 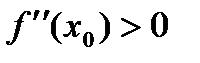, то график на (a,b) имеет выпуклость вниз (вверх если ).

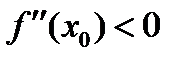20.Ф-ии многих перемен-х:непрерыв-ть и диф-сть.Диф-ал и частные производ-е сложной ф-ии.Ф-ла Тейлора.Экстремумы ф-ии многих перемен-х.Отображение f:X→Rⁿ,где X 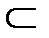Rⁿ наз.ф-ей многих перемен-х.А 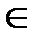R наз.пределом ф-ии u=f(x₁,…,x_n), при(x₁,…,x_n)→(а₁,…,а_n),если ε>0, 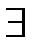δ>0,что x 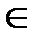D(f)Λ0<ρ(x,a)<δ:│f(x)-A│<ε.Ф-ия u=f(x)наз.непрерыв-ой в т-ке x₀ 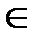D(f),если lim_x→x0f(x)=f(x₀).Ф-я f:X→Rⁿ,X 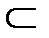Rⁿназ. равномерно непрерывной на мн-ве X,если ε>0, 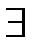δ>0;x₁,x₂ 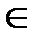X, ρ(x₁,x₂)<δ:│f(x₁)-f(x₂)│<ε.Ф-я f:X→Rⁿ,X 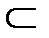Rⁿ наз.диф-ой во внутр.т-ке x₀ 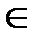X,если приращение ф-и в этой т-ке ∆f(x₀)=f(x₀+∆x)-f(x₀)=A₁∆x¹+A₂∆x²+…+A_n∆xⁿ+O(ρ),где 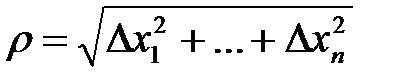. Част.произв.ф-и f по х:¶f/¶x_i=lim(Δx_if/Δx_i),где Δx_if-частн.приращение,Δx_i приращение арг-та x.Связь диф-ти с 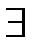частных производ-х:●ф-ция диф-ма,когда 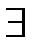производ-я в т-ке (обратное верно);●ф-ция диф-ма в т-ке=>в этой т-ке 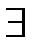частные производ-е(обратное не верно).Рассм-им отображ-ие f:Rⁿ→Rⁿ,f=(f₁,…,f_n),f₁(x₁,…,x_n)…f_m(x₁,…,x_n).М-ца,эл-ты кот. явл. частные производные координат. ф-ий наз. м-цей Якоби. 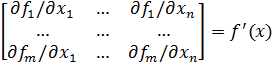.Ф-ла Тейлора:Пусть ф-ия u=f(x₁,…,x_n)=f(x) им.первые частные производ-е до порядка m включит-о, тогда справедливы след. ф-лы ∆f(x₀)=f(x₁,…,x_n)-f(x¹₀,…,xⁿ₀)= 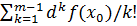+z_m(x₀x),где z_m(x₀x)-остаточный член ф-лы Тейлора.Т.(о диф-ти сложной ф-и)если ф-ии φ_i(t¹,...,t^k)диф-мы в т-ке t₀=(t¹₀,...,t₀^k),а ф-ия u=f(x)=f(x¹,…,xⁿ)диф-ма в соотв.т-ке x₀=(φ₁(t₀),…,φ_n(t₀)),то и сложная ф-я u=f(φ₁(t₁,…,t_k),…,φ_n(t₁,…,t_k)),диф-ма в т-ке t₀.T.(Необход.усл-е extr).Пусть ф-я f:D→Rим.частн произв-е по всем перем-м х и т-ка M₀(x¹₀,…,xⁿ₀)-т-ка extr f,то необход. Выполнение след.рав-в ¶f/¶x₁(M₀)=0,…,¶f/¶x_п(M₀)=0.Д-во: M₀-т-ка max f(x₁,…,x_n). 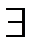U(M₀), x 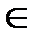U(M₀),f(x)≤f(x₀).f(x₁,…,x_n)≤f(x¹₀,…,xⁿ₀).Возьмем т-ку М' с координатами М’(x₁,x²₀,…,xⁿ₀)(где x₂=x²₀,…,x_n=xⁿ₀).Согласно опр-ю max(т-ка M₀т-ка max,если ∆f(M₀)=f(x¹,…,xⁿ)-f(x¹₀,…,xⁿ₀)≤0)в частности и для т-ки M' выпол.нер-во f(x₁,x²₀,…,xⁿ₀)≤f(x¹₀,…,xⁿ₀).Ф-ия f(x₁,x²₀,…,xⁿ₀)=φ(x₁)-ф-ия одной переменной x₁,φ(x₁)≤ φ(x₀¹) =>согласно опр-ю max ф-ии одной переменной т-ка x¹₀–т-ка max φ(x₁)=>производная φ'(x₁)=0=> 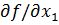(x₀)=0.Анологично док-ся и остальные соотнош-я■.Т.(Дост. усл. extr)Пусть ф-я r=f(x,y)им.непрерыв.частные производ-ые в окр-ти т-ки U(M₀(x₀,y₀)),тогда если M₀(x₀,y₀)стационар.т-ка,т.е.такая что df(x₀,y₀)=0 и выполн. след.усл-я: 1. J₂= 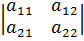>0, a₁₁= 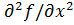(M₀)>0, a₁₂= 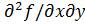(M₀), a₂₂= 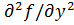(M₀), a₂₁= 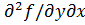(M₀), то т-ка M₀-т-ка локального min;2.a₁₁<0,J₂>0,то т-ка M₀-т-ка локального max;3.J₂<0,то M₀ в нет extr;4.J₂=0-особый случай.Опр.т-ка M₀(x¹₀,…,xⁿ₀) наз.т-кой уловного max(min)ф-ии U=f(x₁,…,x_n),если 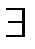U(M₀) 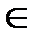D(f),что x 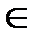U(M₀)и (x₁,…,x_n), удовлетвор. сис-ме f_i(x₁,…,x_n)=0 (i=1…n) выполн. нер-во: f(x)≤f(x₀) или f(x₁,…,x_n)≤f(x¹₀,…,xⁿ₀) (для min f(x)≥f(x₀) или f(x₁,…,x_n)≥f(x¹₀,…,xⁿ₀))

М-д множителей Лагранжа: рассм ф-ю Лагранжа Ф(x₁,…,x_n,λ₁,…,λ_m)=f(x₁,…,x_n)+ λ₁F₁(x₁,…,x_n)+…+λ_nF_n(x₁,…,x_n)(*),где F_i(x)=0(i=1…n)-ур-ия связи. Находим т-ки подозрительные на экстр-м для ф-и Лагранжа: 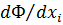=0;F_i(x₁,…,x_n)=0,где(i=1…0).Эта система имеет n+m переменных.Предположим,что она им.реш-е x₀¹,…,x₀ⁿ,λ₁,…,λ_m.Ф-я (*)и конкретно найденные λбудет зависеть от переменных.Т-ка M(x¹₀,…,xⁿ₀)подозрит на extr.

21. Интеграл РиманаDf: Число J называется определенным интегралом для функции f(х) на отрезке [a,b] , если 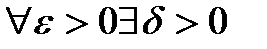такие что если произвести разбиение любое P[a,b] на частичные отрезки с мелкостью разбиения 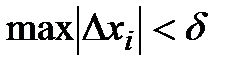будет выполнятся неравенство: 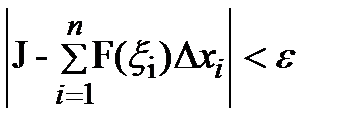, т.е J – определ интеграл если 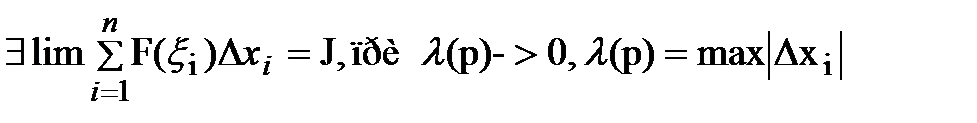- мелкость разбиения, причем предел не зависит ни от разбиения не от выбора точек 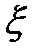на каждом граничном отрезке .Символически записывается 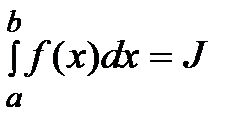- интеграл Римана. Если существует интеграл от f(x), то ф-ция называется интегрируемой по Риману.

Т(необход усл интегрируемости): Для того чтобы ф-ция былая интегр-ма по Риману на [a,b], необходимо чтобы она была ограничена на нем. Усл ограниченности ф-ции является необходимым усл интегрируемости но не достаточным.

Критетий Лебега: Ф-ия f интегрируема по Риману на на [a,b], тогда и только тогда, когда f ограничена на нем и множесто всех точек разрыва ф-ции на на [a,b] есть множесто меры ноль.

Классы инт-х ф-ий: 1-ай класс ф-я непр-на на отрезке=>инт-ма на нём, 2ф-я монотонна на отрезке=> инт-ма на нем, 3ф-я огр-на на отрезке и имеет конеч. число точек разрыва => инт-ма на нем. Св-ва: 1) если ф-и f и g интегр-мы на [а;в] то их линейная комбинация 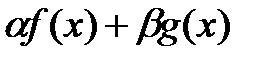также интегр-мы 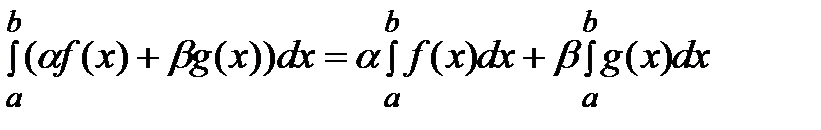.2) если ф-и f и g интегр-мы на [а;в] то f *g – интегр-я ф-я.След-во 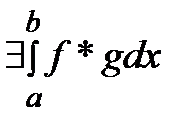3) если ф-и f интегр-ма на [а;в] и а<с<в то 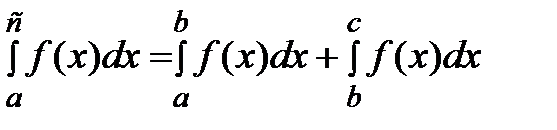. Ф-ла Ньютона-Лейбница: 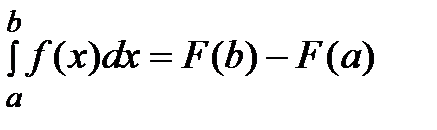.где F(x) одна из первообразных f(x)

Замена переменной:Если f(х) –непрерыв диф на [а,b] и 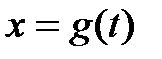-непрерыв диф на 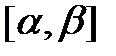то 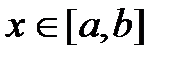причем 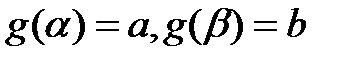, то имеет место формула: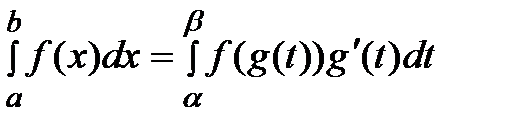

Пусть F(x) – первообразная для ¦(x). По ф-ле Ньютона-Лейбница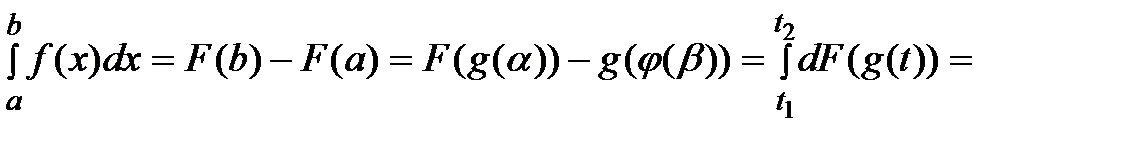

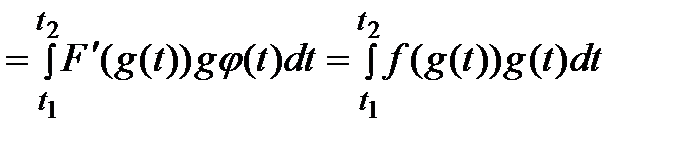
Интегрирование по частям: Пусть u и v непрерывно дифференц. На [a,b], то .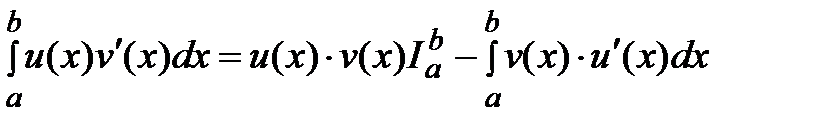

Кратный интеграл: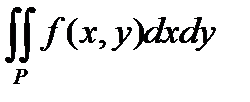

Сведение к повторным интегралам:1)(случай прямолин.обл.) Т. пусть f(x,y) интегр-ма на 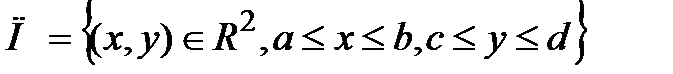, сущ-т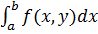 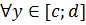, тогда ф-я 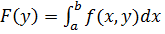интегр-ма на [а;b] и имеет место ф-ла 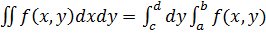dx 2) Т.(случай криволинейной обл-ти) пусть f(x,y) интегр-ма на 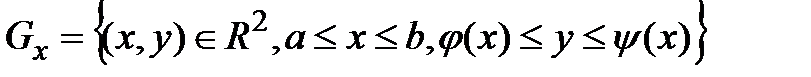, сущ-т 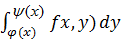, то имеет место ф-ла 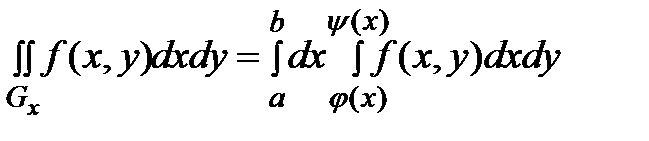, 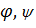-непр.

Выч-ся путем сведения их к однородным итегралам. В 2-х инт-лах => переход к полярным координатам. 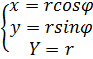тогда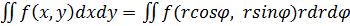

в 3-х инт-лах => переход к цилиндрическим корд. 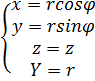и сферическим корд.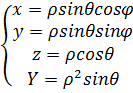

и тогда 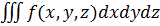заменится аналогично 2-му интегралу.