Пересечение цилиндра проецирующей плоскостью

Задача. Построить нормальное сечение цилиндра плоскостью, проходящей через т. М. Дан цилиндр наклонный эллиптический с круговым основанием и осью, параллельной плоскости П₁.

Поскольку ось цилиндра — фронтальная прямая, а образующие ей параллельны, следовательно, плоскость нормального сечения фронтально-проецирующая плоскость б (рис. 86). Вырожденная ее проекция б₂ проходит на эпюре через проекцию М₂ точки М перпендикулярно фронтальной проекции оси цилиндра. В сечении цилиндра плоскостью б получается замкнутая плоская кривая, называемая эллипсом. Фронтальная проекция эллипса сечения сливается с прямой б₂ и ограничена точками 1₂ и 2₂, лежащими на контурных образующих цилиндра. Горизонтальные проекции точек 1 и 2 находим на горизонтальных проекциях соответствующих образующих цилиндра. Точки 1 и 2, как видно из чертежа, являются самой верхней и самой нижней точками фигуры сечения, кроме того, они являются концами одной из осей эллипса сечения. Вторая ось эллипса сечения 3 4 перпендикулярна первой и делит первую пополам. Значит, на фронтальной плоскости проекций ось 3 4 вырождается в точку 3₂≡4₂, лежащую на проекции оси цилиндра. Горизонтальные проекции этих точек находим из условия принадлежности их образующим цилиндра. Точки 3 и 4 являются одновременно самой ближней и самой дальней точками сечения соответственно. И кроме того, точки 3 и 4 являются точками границы видимости для горизонтальной проекции, так как лежат на контурных образующих горизонтальной проекции цилиндра.

Чтобы точнее обвести фигуру эллипса сечения, в промежутке между построенными характерными точками выберем произвольные промежуточные точки, например, 5, 6 и 7, 8 (зададим их произвольно на фронтальной проекции сечения). Горизонтальные их проекции строятся из условия принадлежности их соответствующим образующим цилиндра.

Рис. 86

Соединив достроенные точки по лекалу, получим горизонтальную проекцию эллипса сечения цилиндра плоскостью. Для определения видимости фигуры сечения и цилиндра на горизонтальной проекции, следует на фронтальную проекцию смотреть по стрелке К. Секущую плоскость б и цилиндр считаем непрозрачными. Нижнее основание цилиндра и часть цилиндра между ним и секущей плоскостью оказывается под плоскостью и, следовательно, на горизонтальной проекции не видимы (обводим штриховой линией). Эллипс сечения, лежащий в секущей плоскости, будет виден на участке 3 1 4, так как эта его часть лежит на верхней видимой половине цилиндра. А участок эллипса 4 2 3 лежит на нижней невидимой половине цилиндра и поэтому невидим.

На этом примере хорошо разобрать и запомнить следующее правило: невидимые линии контура тела переходят в невидимые линии фигуры сечения и, наоборот, видимые контуры тела переходят в видимую линию фигуры сечения.

На фронтальной проекции плоскость и эллипс сечения сливаются в прямую, поэтому вопрос видимости не возникает.

Построим натуральную величину эллипса сечения.

Сделать это можно несколькими способами, например, переменой плоскости проекций П₁, вращением вокруг фронтально-проецирующей оси i. Выполним построение вторым способом. При этом фронтальные проекции точек эллипса сечения перемещаются по окружностям с центрами в i₂, а горизонтальные проекции перемещаются по прямым, перпендикулярным к i₁.

Конические сечения

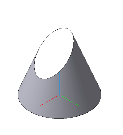
1. Эллипс (окружность) – рис. 87.

Если секущая плоскость не параллельна ни одной из образующих конуса, т. е. пересекает все образующие, то в сечении получается замкнутая кривая, называемая эллипсом. В частности, если секущая плоскость перпендикулярна оси конуса вращения, то в сечении получается окружность (рис. 87). Угол наклона секущей плоскости к оси конуса в этом случае больше угла наклона образующей конуса к оси.

Эллипс Окружность

Рис. 87

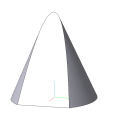
2. Парабола (прямая) – рис. 88.

Если секущая плоскость параллельна одной образующей конуса (на рис. 88 - SА), то в сечении получается парабола. Это разомкнутая кривая, так как плоскость не пересекает образующую SА даже в продолжении; и имеет одну ветвь, так как верхнюю полу конуса плоскость тоже не пересекает. В частности, если плоскость проходит через вершину конуса, в сечении получается прямая SА, по которой плоскость касается конуса.

Можно также сказать, что парабола получается, если секущая плоскость наклона к оси конуса под углом, равным углу наклона образующей к оси.

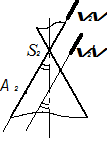
Парабола Прямые

Рис. 88

3. Гипербола (две прямых) – рис. 89.

Если секущая плоскость параллельна двум образующим, например, SА и SВ (рис. 89), то в сечении получается гипербола. Точки 1 и 2 — вершины двух ветвей гиперболы. В частности, если плоскость проходит через вершину конуса, то в сечении получается пара пересекающихся прямых (образующих конуса).

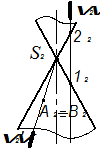
Рис. 89