Занятие № 19. Пошаговый контроль точности. Метод Кутты-Мерсона

Цель - ознакомить студентов с пошаговым контролем точности и методом Кутты-Мерсона решения задачи Коши для обыкновенных дифференциальных уравнений.

Нетрудно понять, что выведение надежных и, в то же вре­мя, простых и эффективных оценок погрешности, гарантирую­щих получение таблицы значений решения у=у(х) заданной точности, является делом малоперспективным, особенно для ме­тодов более-менее высоких порядков. Поэтому главным спосо­бом отслеживания точности при реализации численных процесcов решения задачи Коши остается применение различных полуэмпирических правил, основанных на принципе Рунге.

Будем считать, что при использовании метода р-гопорядка абсолютная шаговая погрешность должна находиться в пределах ε>0. Тогда, согласно принципу Рунге, осуществляется счет по системе узлов 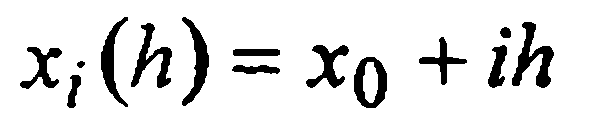с шагом h и по системе узлов 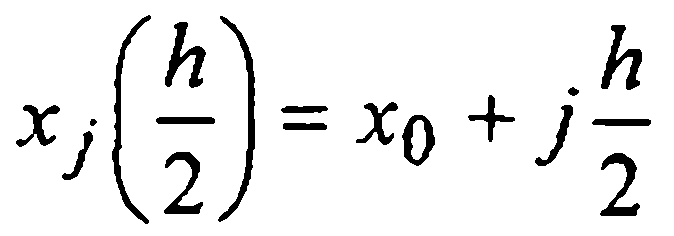— с шагом h/2. При четных j вторая система будет совпадать с первой, т.е. 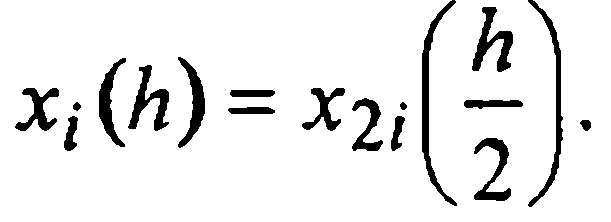Переход от расчетной точки x_i с приближенным значением решения в ней у_iк расчет­ной точке один раз совершается за один шаг длины hи приводит к значению 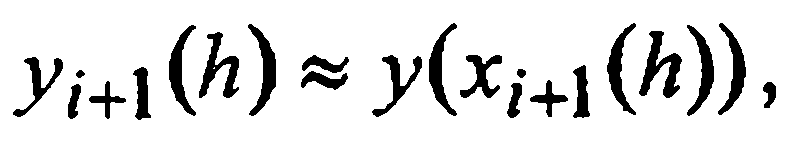другой раз — за два шага длины h/2 («транзитом» через точку 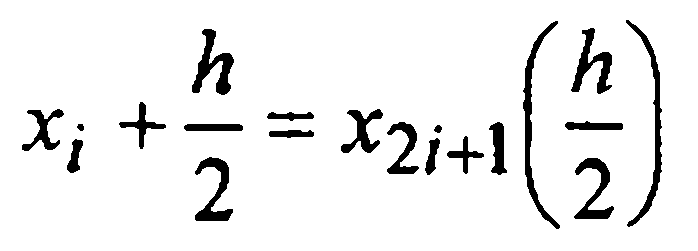со значением 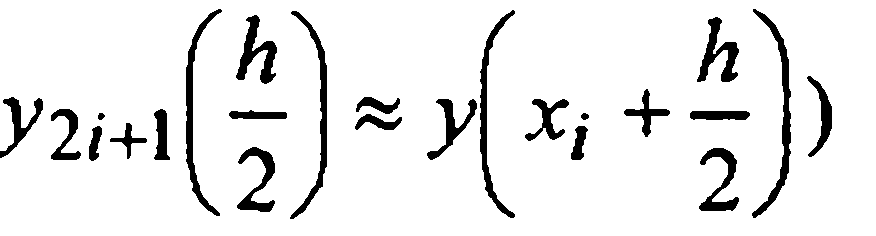и дает значение

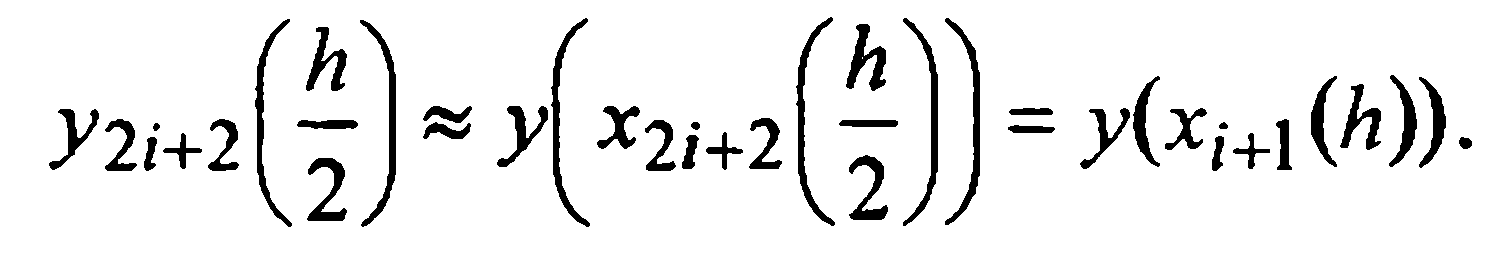
Поправка Ричардсона в таком случае будет составлять величину

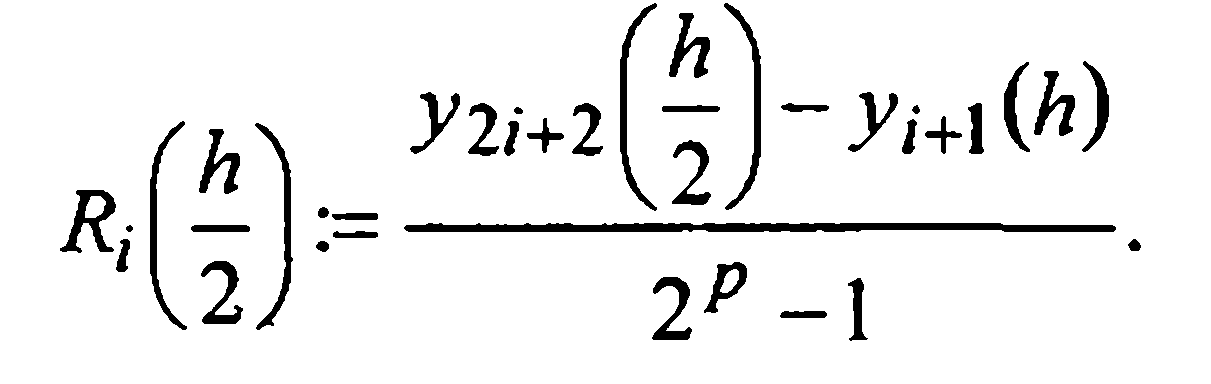(34)

Если величина 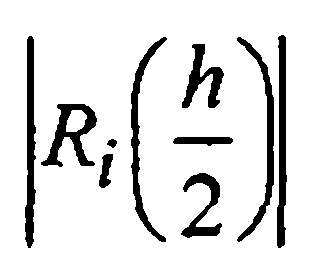меньше заданного ε, то можно считать, что ошибка приближенного равенства 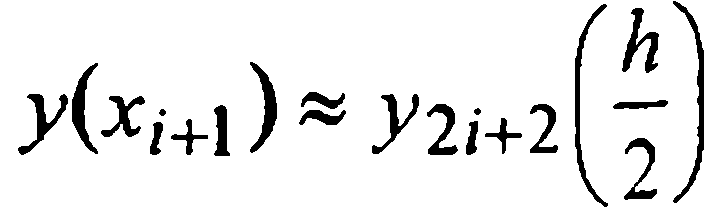не превосходит ε. Если же 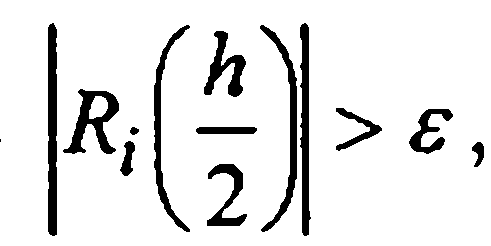то следует уменьшить расчетный шаг h.При условии 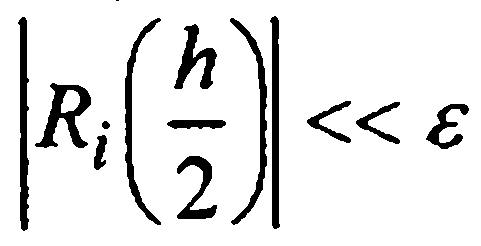стоит попытаться двигаться дальше с более крупным шагом (например, удвоить h).

Пример 2. (продолжение примера 1). Посмотрим, что дает применение принципа Рунге к нескольку простым методам численного решения того же уравнения y'=2х-3yначальным условием у(0) = 1. Из точки х=0 перейдем в точку х=0.2 за один шаг h =0.2 четырьмя одношаговыми методами: явным и неявным методами Эйлера, методом трапеций и методом Хойна — частным случа­ев метода Рунге-Кутты второго порядка. С помощью полученных значе­ний 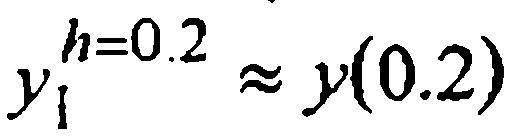и найденных ранее теми же методами в примере 1 значений 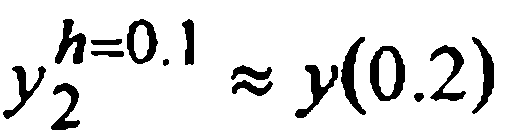подсчитаем поправки Ричардсона

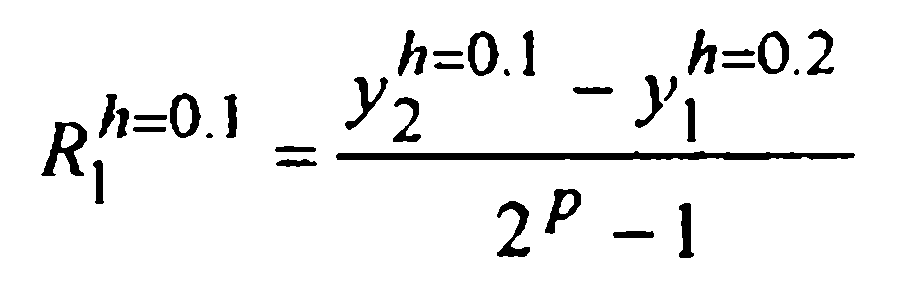
при р=1 для методов Эйлера и р=2 для методов трапеций и Хойна. Эти результаты, а также уточненные прибавлением к значениям 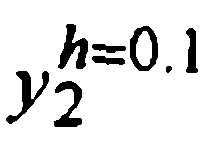попра­вок Ричардсона 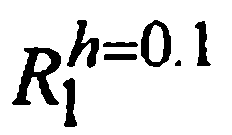приближенные значения 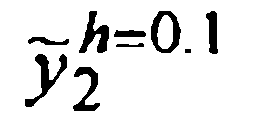решения y(0.2) и их истинные погрешности 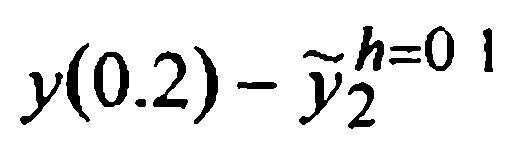сведем в следующую таблицу.

Метод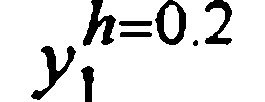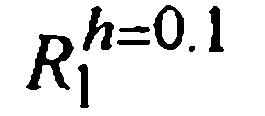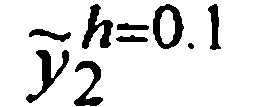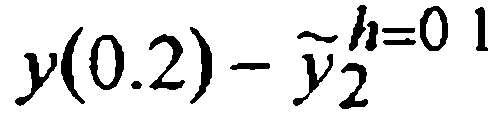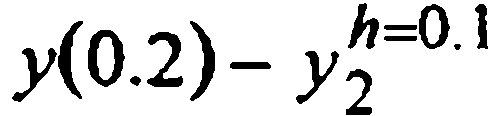
Эйлера (8)	0.4	0.11	0.62	≈-0.04	≈0.07
Неявный Эй­лера (14)	0.675	≈ -0.0407	≈ 0.5936	≈-0.01	≈ -0.05
Трапеций (15)	≈0.5692	≈0.0032	≈0.5820	≈-0.0001	≈0.003
Хойна (16)	0.62	≈ -0.0102	≈0.5793	≈ 0.0026	≈ -0.008

В эту таблицу последним столбцом помещен последний столбец из таблицы результатов примера 1, содержащий погрешности значе­ний 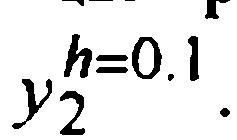Сравнение с ним столбца со значениями поправок Ричардсона показывает, что эти поправки хорошо отражают поведение погрешностей методов (хотя и не дают основания считать их модули оценками погрешностей), а предпоследнего — эффективность уточнения по правилу Рунге-Ричардсона.

Грубо обозначенная здесь технология пошагового контроля точности численного интегрирования дифференциальных уравнений и автоматического выбора расчетного шага при этом на основе двойного счета в такой непосредственной форме говорит о ее значительной «дороговизне». Действительно, предположим, что для решения задачи (1)-(2) применяется четырехэтапныйметод Рунге-Кутты четвертого порядка (33). Тогда вы­полнение одного его шага с контролем точности по правилу Рунге потребует 11 вычислений правой части уравнения (1) (по четыре получения каждого из значени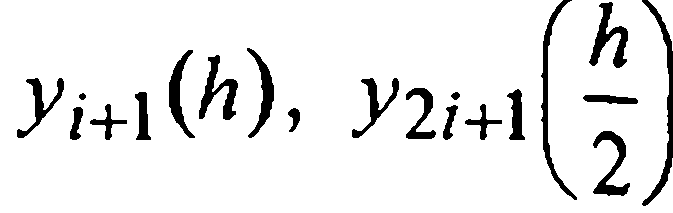й и 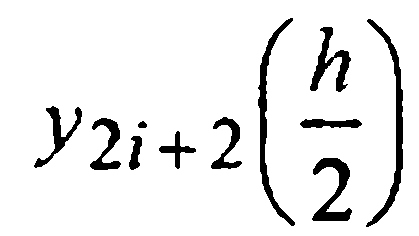минус одно общее для 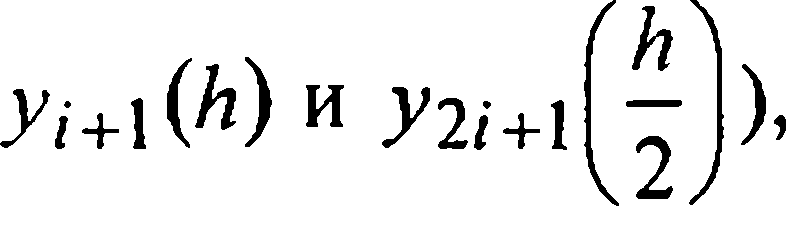весьма затратно.

Более «дешевый», но, возможно, менее строгий способ су­дить о том, достаточно ли малым выбран шаг h расчетов по ме­тоду Рунге-Кутты четвертого порядка (33), — это вычисление при каждом i= 0,1, 2,... величин

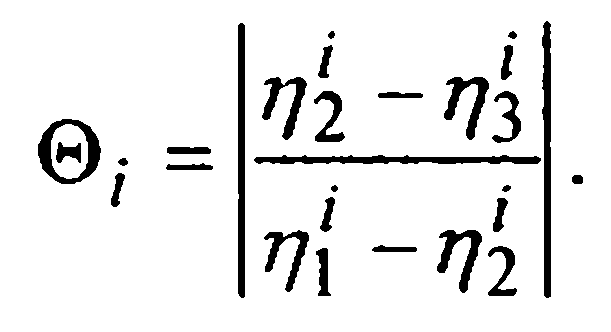
Считается, что если величина Θ_i, не превосходит нескольких со­тых, то можно продолжить вычисления с данным шагом или пы­таться при переходе от i к i+1 его увеличить; в противном случае шаг следует уменьшить, например, вдвое.

Стремление повысить вычислительную эффективность при­вело к появлению различных вычислительных версий методов Рунге-Кутты, благо для этого в семействе методов (32) имеет­ся значительное число свободных параметров. Основные сооб­ражения, положенные в основу этих версий, таковы: нужно по­лучить формулы из семейства методов Рунге-Кутты (32), которые использовали бы одни и те же значения функции — правой части уравнения (1) — и определяли бы разные кон­кретные методы одного порядка (или смежных порядков, напри­мер, четвертого и пятого); при этом, чтобы по разности результа­тов подсчета приближенных значений решения по выведенным близким формулам (с одним и тем же шагом h(!)) можно было судить о точности одного из них.

Приведем один из таких методов, который называется методом Кутты-Мерсона или, иначе, пятиэтапным мето­дом Рунге-Кутты четвертого порядка, а также методов вложенных форм.

На i-ом шаге решения задачи (1)-(2) последовательно вычисляют:

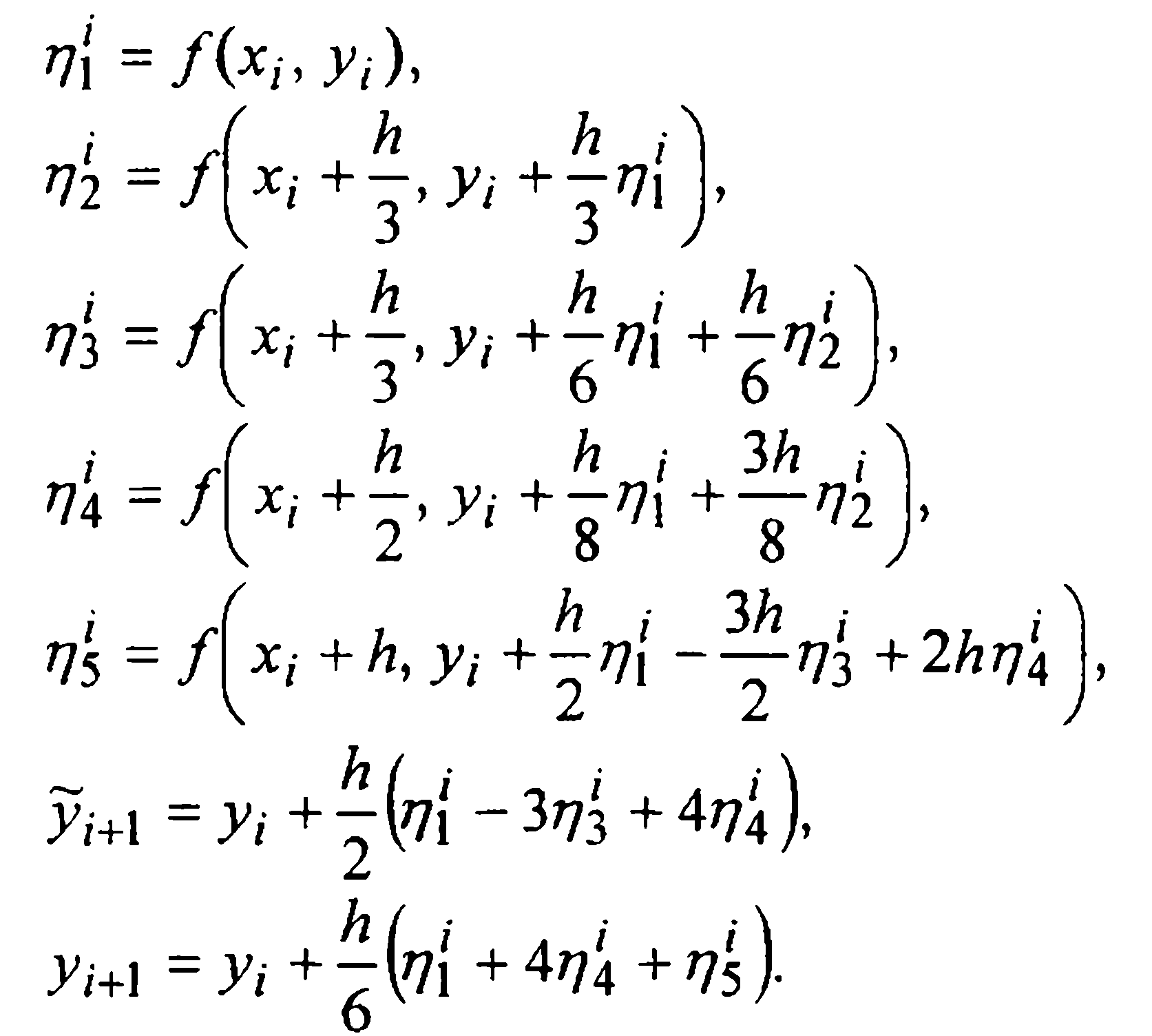
После этого подсчитывают величину

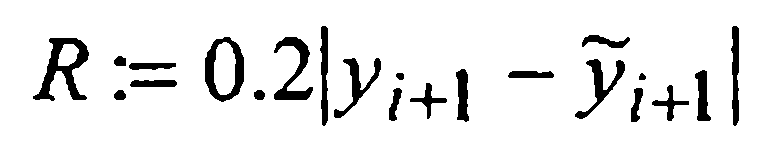
и проводят сравнения. Если значение R окажется больше задан­ного допустимого уровня абсолютных погрешностей ε, то шаг уменьшают вдвое 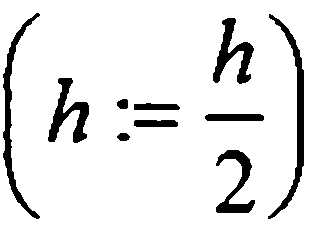и возвращаются к началу второго эта­па, т.е. заново вычисляют 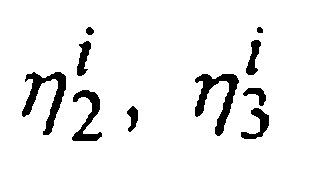и т.д. Если R≤ε, то считают 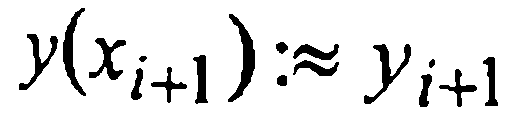с точностью ε. При переходе к следующему шагу делается проверка на возможность увеличить расчетный шаг: если 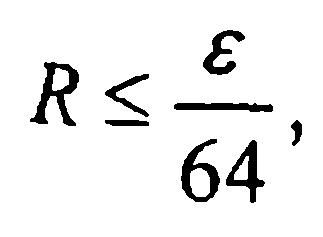то далее расчет ведется с шагом h:= 2h.