Лекція 13.Звичайні диференціальні рівняння

Основні поняття

Означення. Звичайним диференціальним рівнянням називається рівняння, яке пов'язує незалежну змінну х, шукану функцію та її похідні , , …, ,...

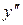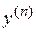Символічно диференціальне рівняння можна записати так:

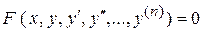(4.1)

або

. (4.2)

Означення. Порядком диференціального рівняння називається порядок найвищої похідної, що входить у рівняння.

Так, наприклад, рівняння

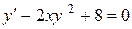є рівняння першого порядку.

Рівняння

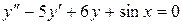є рівняння другого порядку.

Означення. Розв'язком або загальним інтегралом диференціального рівняння називається така функція , яка, після підставлення в рівняння, перетворює його в тотожність.

Диференціальне рівняння першого порядку має вигляд

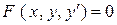. (4.3)

Якщо це рівняння можна розв'язати відносно , то його можна записати у вигляді

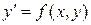. (4.4)

Означення. Умова, що при 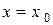функція у повинна дорівнювати заданому числу 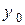, називається початковою умовою, або умовою Коші. Вона записується у вигляді

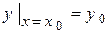або 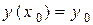. (4.5)

Означення. Задача, у якій потрібно знайти частинний розв’язок рівняння 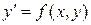, який задовольняє початковій умові 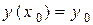, називається задачею Коші.

Означення. Загальним розв’язком диференціального рівняння першого порядку називається функція

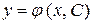, (4.5)

яка залежить від однієї довільної сталої С і задовольняє наступним умовам:

а) вона задовольняє диференціальному рівнянню при будь-якому конкретному значенні сталої С;

б) яка б не була початкова умова 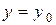при 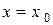, тобто 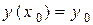, можна знайти таке значення 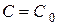, що функція 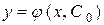задовольняє даній початковій умові.

У процесі знаходження загального розв'язку диференціального рівняння ми можемо прийти до співвідношення вигляду

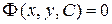, (4.6)

не розв'язаному відносно у. Розв'язавши це співвідношення відносно у, одержуємо загальний розв'язок. Однак не завжди удається виразити у в елементарних функціях; у таких випадках загальний розв'язок залишається в неявному вигляді.

Означення. Рівність вигляду 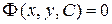, яка неявно задає загальний розв'язок, називається загальним інтегралом диференціального рівняння.

Означення. Частинним розв'язком називається будь-яка функція 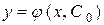, яка утворюється з загального розв'язку 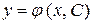, якщо в останньому довільної сталої С придати визначене значення 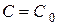. Співвідношення 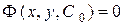називається в цьому випадку частинним інтегралом рівняння.

З геометричної точки зору загальний інтеграл представляє собою сімейство кривих на координатній площині, які залежать від однієї довільної сталої С. Ці криві називаються інтегральними кривими даного диференціального рівняння. Частинному інтегралу відповідає одна крива цього сімейства, яка проходить через деяку задану точку площини.

Розв’язати або проінтегрувати диференціальне рівняння - значить:

а) знайти його загальний розв'язок або загальний інтеграл (якщо початкові умови не задані) або

б) знайти той частинний розв'язок рівняння, який задовольняє заданим початковим умовам (якщо такі є).

Означення. Особливим розв'язком називається такий розв'язок, у всіх точках якого умова єдиності не виконується, тобто в будь-якому околі кожної точки 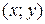особливого розв'язку існують принаймні дві інтегральні криві, які проходять через цю точку.

Особливі розв'язки не утворюються з загального розв'язку диференціального рівняння ні при яких значеннях довільної сталої С (у тому числі і при 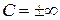).