О других итерационных методах решения слау

В основе построения и изучения или, по крайней мере, понимания многих итерационных методов лежит связь между системами алгебраических уравнений и методами дискретизации дифференциальных уравнений, их порождающими.

В простейшем абстрактном, но далеко не самом общем случае, легко установить такую связь между СЛАУ (6.1) и абстрактным дифференциальным уравнением

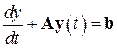(6.25)

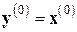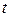с начальным условием , где – абстрактная скалярная переменная, изменяющаяся на промежутке 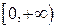, а матрица 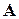и вектор 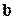те же, что и в уравнении(6.1).

Пусть постоянный вектор 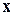и переменный вектор 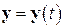– решения задач (6.1) и (6.25) соответственно. Введем вектор

.

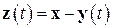Учитывая равенство 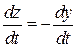, из совместного рассмотрения (6.1) и (6.25) выясняем, что 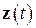удовлетворяет однородному дифференциальному уравнению

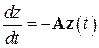
с начальным условием 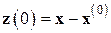. Решением этой начальной задачи служит вектор

,

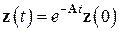и если спектр 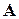лежит в правой полуплоскости (в частности, если, например, матрица 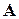положительно определена), то 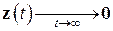при любых 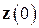. Таким образом, решение 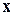системы (6.1) (стационарной задачи) может быть получено как предел при 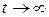решения 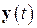задачи Коши (6.25) с произвольным начальным вектором .

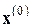Методы приближенного решения статических задач, асимптотически эквивалентных данным задачам для достаточно больших значений искусственной скалярной переменной 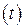, называются методами установления.

Будем далее считать параметром скалярную величину 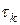, которую применительно к задаче (6.25) можно интерпретировать как шаг (вообще говоря, переменный), с которым на полуоси 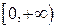фиксируются точки

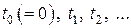
т.е.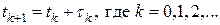

При «замораживании» 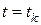уравнение (6.25) принимает вид

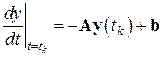(6.26)

Для производной в его левой части при малых 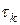на основе определения можно записать приближенное равенство

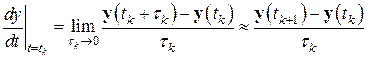
Теперь ясно, что полагая 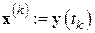(заметим, что 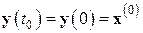), равенство (6.26) можно приближенно заменить равенством

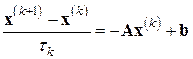(6.27)

которое можно рассматривать как некий явный итерационный процесс. Его называют двухслойным итерационным методом или методом Ричардсона.

Более общий вид семейство двухслойных итерационных методов примет, если ввести в (6.27) невырожденный матричный параметр :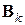

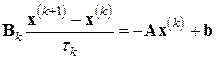(6.28)

Различные конкретные итерационные процессы решения СЛАУ (6.1) (в том числе и все рассмотренные выше) получаются из (6.28) фиксированием матриц В_k и скаляров 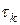. При этом, есл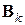и и 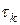не зависят от 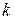, т.е. одни и те же на каждой итерации, то (6.28) определяет стационарный метод, в противном случае – нестационарный. В общем случае, за исключением 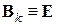, (6.28) – неявный метод.

Выбор параметров 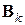, 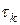в (6.28) осуществляют, добиваясь удовлетворения каких-либо отдельных или совокупности нескольких, возможно в чем-то противоречивых требований таких, как простота, хорошая структура и легкая обращаемость матриц 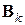и в то же время, как можно более быстрая сходимость последовательности 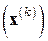к решению 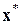системы (6.1). Разумеется, оптимальность или_, скорее, квазиоптимальность некоторых методов рассматриваемого семейства удается установить лишь при очень жестких ограничениях на решаемую систему (6.1).

Так, например, доказано, что если система (6.1) – нормальная с известными границами 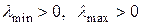спектра ее матрицы коэффициентов, то при заранее зафиксированном (максимальном в реализуемом процессе) числе итераций 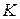метод (6.27) будет обеспечивать наименьшую погрешность, иначе, минимизировать величину 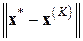, в том случае, когда параметры 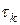вычисляются по формуле

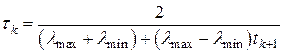(6.29)

где 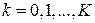, а 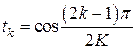– корни полинома Чебышева 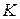-й степени. Совокупность формул (6.27), (6.29) называют явным итерационным методом с чебышевским набором параметров. Имеется обобщение приведенного утверждения и на неявный случай.

Дальнейшее формальное развитие методы установления получают как сугубо неявные методы вида (6.28) с матрицами 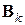, представляемыми в виде произведения простых легко обращаемых (например, ленточных) матриц, в связи с чем такие методы называются методами расщепления. Из методов расщепления наиболее известными являются методы переменных направлений* и попеременно-треугольный метод, неформальное изучение этих методов более целесообразно по месту их применения: при численном решении многомерных задач математической физики.

Рассматриваются также трехслойные итерационные методы (в частности, с чебышевскими параметрами), связывающие уже не два, а три соседних приближения: 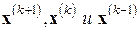. В отличие от предыдущих, такие методы являются двухшаговыми.

Другой большой класс методов итерационного решения СЛАУ (6.1) – это так называемые методы вариационного типа. К ним относятся методы минимальных невязок, минимальных поправок, минимальных итераций, наискорейшего спуска, сопряженных градиентов и т.п. Хорошего понимания и обоснования таких методов можно достигнуть лишь с привлечением теории оптимизации, ибо решение линейной алгебраической системы здесь подменяется решением эквивалентной экстремальной задачи.

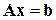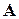А именно, пусть – нормальная -мерная система, т.е. – положительно определенная симметричная матрица, и пусть 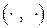– скалярное произведение в пространстве 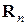. Образуем квадратичный функционал

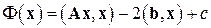(6.30)

где 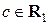– произвольная постоянная. Задача решения нормальной системы (6.1) и задача минимизации функционала (6.30) эквивалентны. Действительно, нормальная системаимеет и притом единственное решение; обозначим его 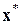. Тогда при любом векторе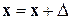

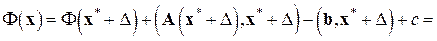
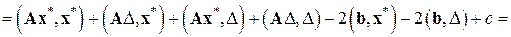
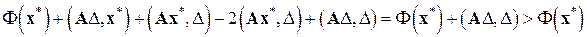
в силу самосопряженности и положительности 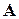; значит,

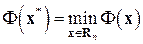
Теперь можно применять различные методы численной минимизации функционала 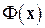(в конечном итоге, функции переменных )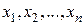

Одним из наиболее популярных и хорошо разработанных методов подобного типа является метод сопряженных градиентов. Приведем без вывода алгоритм, может быть, недостаточно подробный, но вполне определенный, чтобы с его помощью можно было решать нормальные СЛАУ (6.1) таким способом.

Фигурирующим в нем переменным можно придать следующий оптимизационный смысл:

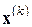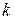– -е приближение к искомому ;

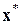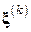– невязка 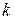-го приближения, играющая роль антиградиента функции ;

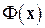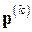- направление минимизации функции 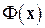в точке ;

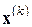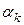– коэффициент, обеспечивающий минимум 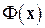в направлении вектора ;

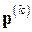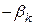– коэффициент при 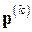в формуле для вычисления направления 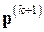, обеспечивающий -сопряженность векторов 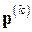и 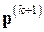( 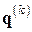– вспомогательный вектор).

Алгоритм МСГ

Шаг 1.1. Задать 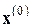(начальный вектор) и число 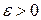(допустимый уровень абсолютных погрешностей).

Шаг 1.2. Вычислить вектор 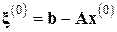(невязка начального приближения).

Шаг 1.3. Положить 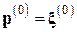, 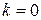(номер итерации).

Шаг 2.1. Вычислить вектор .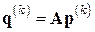

Шаг 2.2. Вычислить скаляр 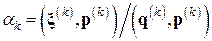(шаговый множитель).

Шаг 2.3. Вычислить вектор 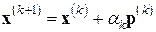(очередное приближение).

Шаг 2.4. Вычислить вектор 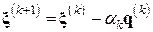(невязка 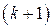-го приближения*).

Шаг 2.5. Проверить выполнение неравенства 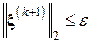, если «да», остановить работу алгоритма и вывести результаты.

Использование такого выражения невязки 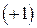позволяет обходиться без вычисления вектора 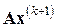. Однако нужно понимать, что подобная экономия в арифметических операциях может отразиться на вычислительной устойчивости метода.

Шаг 3.1. Вычислить скаляр .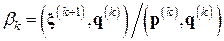

Шаг 3.2. Вычислить вектор 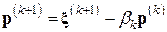(новое направление минимизации).

Шаг 3.3. Положить 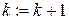и вернуться к шагу 2.1.

Интересно определить место, которое занимает этот метод в общей классификации методов решения линейных алгебраических систем. Дело в том, что метод сопряженных градиентов, являясь по форме итерационным. фактически должен быть отнесен к прямым методам, ибо доказано, что с его помощью минимум квадратичной функции (6.30) от переменных, иначе, решение n-мерной линейной системы (6.1), достигается ровно за шагов при любом начальном векторе 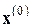. Применяют же метод сопряженных градиентов именно как итерационный метод (что видно и из приведенного алгоритма), имея в виду два обстоятельства.

Во-первых, реальный вычислительный процесс может быть довольно далек от идеального и, вследствие неизбежных ошибок округления, на n-м шаге может быть не достигнута нужная точность. Во-вторых, если размерность n решаемой задачи велика, то число шагов, достаточное для получения решения системы с нужной точностью (т.е. выход по критерию 2.4), может оказаться значительно меньшим этой теоретической величины.

Простейший вариант метода минимальных невязок определяется совокупностью формул

, , .

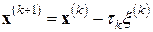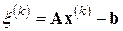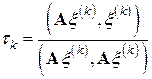Его можно рассматривать как явный двухслойный итерационный процесс (6.27), в котором параметр 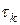на каждом итерационном шаге 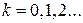выбираем таким, чтобы минимизировалась евклидова норма невязки 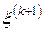получаемого приближения .

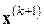Действительно, вычтем из вектора 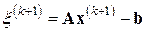вектор 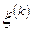. Имеем

,

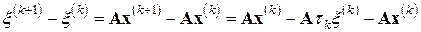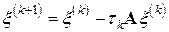
Возводя последнее равенство в квадрат (в смысле скалярного умножения векторов), получаем

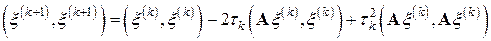
или, что то же,

.

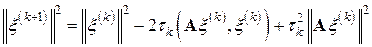Легко видеть, что минимум этой положительной квадратичной функции (значит, и величины 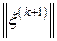) достигается именно при указанном в записи метода значении .

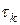В случае нормальной системы для метода минимальных невязок можно получить ту же оценку скорости сходимости, что и для метода простой итерации

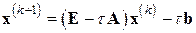
при оптимальном значении параметра 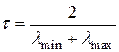(в предположении, что известны границы 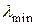и 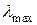спектра матрицы ).

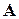Рассмотренные здесь методы далеко не исчерпывают все многообразие итерационных способов решения СЛАУ. В частности, нами совсем не затрагивалась проблема решения больших разряженных систем, где на первый план выходят блочные методы, максимально сохраняющие исходную разреженность матриц (см., например).