Аппроксимация зависимостей

Постановка задачи, основные понятия

Одной из важнейших задач, возникающих в процессе математического моделиро­вания, является вычислений значений функций, входящих в математическое описание модели. Используемые в математических моделях функции зачастую задаются табличным способом, например, если они получены в результате эксперимента.

x	f (x)
x0	f0
x1	f1
x2	f2
. . .	. . .
xn	fn

Выбранные значения аргумента x называются узлами таблицы. В общем случае узлы не являются равноотстоящими. При проведении вычислительных работ обычно воз­ни­­кает необходимость "сгущать" эти таблицы, т.е. вычислять функцию для значений ар­гу­мента, не совпадающих с теми, которые попали в таблицу. Эта проблема решается путем замены функции f(x) , для которой может быть даже неизвестно анали­ти­­чес­кое выраже­ние, некоторой функцией 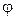(x), имеющей сравнительно несложный аналитический вид и которая в некотором смысле близка к f(x). Приближение функции f(x) более прос­той функцией 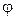(x) называется аппроксимацией. Близости этих функций добиваются вве­дением в аппрокси­ми­ру­ю­щую функцию 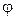(x) свободных параметров c₀, c₁, c₂, ..., c_n. Критерии «близости» аппроксимирующей функции 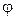(x) к неизвестной функции f(x) могут быть самые различные. Например, это может быть равенство значений 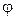(x) и f(x) в узлах таблицы, или минимум суммы квадратов разности между этими значениями. Для аппроксимации по первому критерию применяются полиноми­аль­ные и сплайновые методы; второй критерий используется методом наименьших квад­ратов.

Задачей интерполяции является построение аппроксимирующей функции 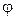(x) и нахождение по ней приближенных значений табличной функции f(x) при аргументах x, не совпадающих с узловыми, но содержащихся в интервале ( x₀, x_n). Эти значения аргу­мента в дальнейшем будем называть точками интерполяции. Если же аппрокси­миру­ющую функцию вычисляют для точек, расположенных вне интервала [x₀, x_n], то такая задача называется экстраполяцией.