Елементи лінійної алгебри та аналітичної
Геометрії
| Назва | Формули та позначення |
| Визначник 2-го порядку |  |
| Визначник 3-го порядку |  |
| Визначник 3-го порядку у вигляді розкладу його за елементами першого ряд-ка |  |
 | Формули Крамера  де де     |
| Розклад вектора за базисом | |
| Алгебраїчний запис | Геометрична ілюстрація |
 |  x=OA= прOx ā, y=OB= прOy ā x=OA= прOx ā, y=OB= прOy ā |
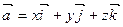 |  x=OA= прOx ā, y=OB= прOy ā, z=OC= прOz ā x=OA= прOx ā, y=OB= прOy ā, z=OC= прOz ā 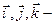 орти орти |
| Лінійні операції над векторами, заданими в координатній формі | |
| Назва операції | Виконання операції |
Додавання векторів 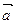 та та  | 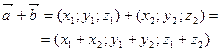 |
Віднімання векторів 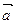 та та  |  |
Множення вектора 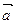 на скаляр λ на скаляр λ |  |
Лінійна комбінація векторів 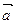 та та  |  |
Основні види добутків векторів  ; ; 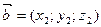 ; ; 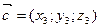 | |||
| Назва і позначення | Означення | Координатна форма | Резуль-тат |
Скалярний добуток векторів 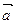 та та  : :  |   або або 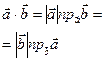 |  | число |
Векторний добуток:  | 1.  2. 2. 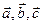 - права трійка; - права трійка;  3. 3.  |  або або 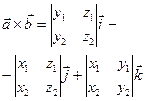 | вектор |
Мішаний добуток векторів 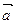 , ,  , , 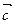 : :  |  | 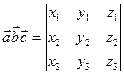 | число |
Основні формули векторної алгебри, які використовують для обчислення геометричних величин  | ||
| Назва | Векторна форма | Координатна форма |
Довжина вектора 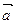 |  |  |
Орт вектора 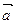 |  | 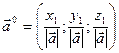 |
Напрямні косинуси вектора 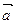 |  , , 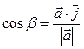 , ,  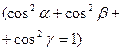 | 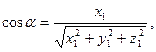 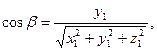  |
Косинус кута між векторами 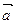 та та  |  |  |
| Площа трикутника АВС |  де де  , , 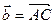 |  |
| Об’єм трикутної піраміди SABC | 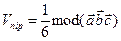   ) ) |  |
| Види рівнянь прямої на площині | ||
| Вихідні дані | Вид рівняння | Назва рівняння |
  – точка прямої; – точка прямої;  – напрямний вектор прямої – напрямний вектор прямої |     | Векторне рівняння прямої Параметричні рівняння прямої Канонічне рівняння прямої |
Дві точки прямої  , ,   | 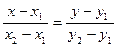 | Рівняння прямої, що проходить через дві точки |
 Точки А(а;0) і В(0;b) прямої розміщені на координатних осях Точки А(а;0) і В(0;b) прямої розміщені на координатних осях |  | Рівняння прямої у відрізках на осях | |
 Точка Точка  прямої; кут φ, який утворює пряма з додатним напрямом осі ОХ а) прямої; кут φ, який утворює пряма з додатним напрямом осі ОХ а)  б) б) |   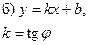 | Рівняння прямої з кутовим коефіцієнтом |
Точка  прямої; вектор прямої; вектор  =(А;В), перпендикулярний до прямої =(А;В), перпендикулярний до прямої |   | Рівняння прямої, що проходить через задану точку перпендикулярно до вектора  Загальне рівняння прямої Загальне рівняння прямої |
| Взаємне розміщення двох прямих на площині | |||
| Вихідні дані | Кут між прямими | Умова паралельно-сті прямих | Умова перпендикуляр-ності прямих |
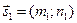 , ,  - напрямні вектори прямих - напрямні вектори прямих 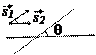 |  |  |  <=> <=>  |
 , ,  - вектори нормалей прямих - вектори нормалей прямих 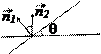 |  | 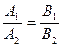 |  <=> <=> 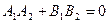 |
| k1,k2 – кутові коефіцієнти прямих |    | 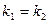 |  |
| Канонічні рівняння кривих другого порядку | ||
| Назва кривої | Геометричне зображення у прямокутній системі координат і основні характеристики кривої | Канонічне рівняння кривої та основні залежності між параметрами |
| Коло | 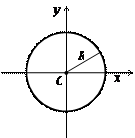 О – центр кола; R – радіус кола. О – центр кола; R – радіус кола. |  R - радіус R - радіус |
| Еліпс |  А1(-а; 0), А2 (а; 0), В1(0; -b), В2 (0;b) – вершини еліпса; F1 (-c; 0), F2 (c; 0) – фокуси еліпса А1(-а; 0), А2 (а; 0), В1(0; -b), В2 (0;b) – вершини еліпса; F1 (-c; 0), F2 (c; 0) – фокуси еліпса | 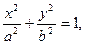 а – велика піввісь; b – мала піввісь (b<a); c – фокальна піввісь; c2=a2-b2; ексцентриситет а – велика піввісь; b – мала піввісь (b<a); c – фокальна піввісь; c2=a2-b2; ексцентриситет  , ,  |
| Гіпербола |  А1(-а; 0), А2(а; 0)– вершини гіперболи; F1 (-c; 0), F2 (c; 0) – фокуси гіперболи А1(-а; 0), А2(а; 0)– вершини гіперболи; F1 (-c; 0), F2 (c; 0) – фокуси гіперболи |  а – дійсна піввісь; b – уявна піввісь; c – фокальна піввісь; c2=a2+b2; ексцентриситет а – дійсна піввісь; b – уявна піввісь; c – фокальна піввісь; c2=a2+b2; ексцентриситет  , ,  рівняння асимптот: рівняння асимптот:  |
| Парабола | О (0;0) – вершини параболи; F  - фокус параболи; - фокус параболи;  KL – директриса параболи KL – директриса параболи |  , p=FL – параметр параболи; ексцентриситет , p=FL – параметр параболи; ексцентриситет  рівняння директриси: рівняння директриси: 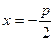 |
Запитання для самоконтролю
1. Що називається визначником другого і третього порядку? Як вони обчислюються?
2. Дайте означення мінора і алгебраїчного доповнення елемента визначника.
3. Сформулюйте властивості визначників третього порядку.
4. Запишіть формули Крамера для розв’язання систем лінійних алгебраїчних рівнянь.
5. Що називається вектором і модулем вектора?
6. Що називається ортом вектора?
7. Які вектори називаються: колінеарними? компланарними? рівними?
8. Які операції над векторами називаються лінійними? Як вони виконуються?
9. Що називається скалярним добутком векторів? Які його властивості?
10. Як виражається скалярний добуток векторів у координатній формі?
11. Який механічний зміст скалярного добутку?
12. Як знайти кут між двома векторами?
13. Як знайти проекцію вектора на вектор?
14. Яка умова перпендикулярності двох векторів?
15. Яка умова колінеарності двох векторів?
16. Дайте означення векторного добутку двох векторів. Які його властивості?
17. Запишіть формулу для обчислення векторного добутку векторів в координатній формі.
18. Який геометричний і механічний зміст векторного добутку двох векторів?
19. Що називається мішаним добутком трьох векторів? Які його властивості і геометричний зміст?
20. Що називається рівнянням лінії на площині?
21. Які види рівнянь прямої площині Ви знаєте? Запишіть і виведіть кожне з них?
22. Як визначити кут між двома прямими?
23. Які умови паралельності і перпендикулярності двох прямих?
24. Як знайти відстань від точки до прямої?
25. Які криві другого порядку Ви знаєте? Дайте означення кожної з них, виведіть їх рівняння.
Рекомендована література:[1],розділ1; [5],ч.1,практичні заняття 2-6, 10, 11, 15-19.
Приклад 1.1.Розв’язати систему рівнянь

Розв’язання.Складаємо і обчислюємо визначник системи Δ, а також допоміжні визначники  ,
,  і
і  .
.

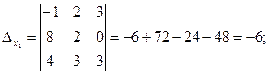


За формулами Крамера знаходимо:



Розв’язок системи 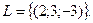
Приклад 1.2. Дано координати вершин піраміди А(2;-1;3), В(1;1;1), С(0;0;5), Д(4;-1;5). Знайти:
а) координати векторів  та їх модулі;
та їх модулі;
б) проекцію вектора  на вектор
на вектор  ;
;
в) 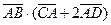 ;
;
г) кут між векторами  та
та 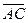 .
. 
Розв’язання.а) Знаходимо координати векторів та їх модулі:

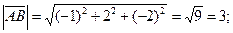
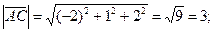

б) Проекцію вектора  на вектор
на вектор  знайдемо за формулою
знайдемо за формулою
де  ×
×  – скалярний добуток цих векторів.
– скалярний добуток цих векторів.
Оскільки  ×
×  = (-1)×2 + 2×0 + (-2)×2= -6, а
= (-1)×2 + 2×0 + (-2)×2= -6, а  то
то 
в) Знайдемо спочатку координати векторів 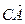 ,
,  та
та 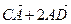 :
: 


Тоді 
г) Оскільки внутрішній кут φ при вершині А трикутника АВС – це кут між векторами  і
і 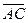 , то
, то 
 ,
, 
Отже, шуканий кут дорівнює  =
=  , тобто вектори
, тобто вектори  і
і 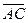 – перпендикулярні.
– перпендикулярні.
Прикллад 1.3. Обчислити роботу, яку виконує сила  =(1;-3;2) при прямолінійному переміщенні матеріальної точки з положення А(0;1;0) в положення В(1;0;1).
=(1;-3;2) при прямолінійному переміщенні матеріальної точки з положення А(0;1;0) в положення В(1;0;1).
Розв’язання.Роботу сили  по переміщенню матеріальної точки з положення А в положення В знайдемо за формулою
по переміщенню матеріальної точки з положення А в положення В знайдемо за формулою  .
.
Знайдемо координати вектора переміщення  =(1;-1;1). Тоді А=1×1+(-3)×(-1)+2×1=6.
=(1;-1;1). Тоді А=1×1+(-3)×(-1)+2×1=6.
Приклад 1.4. Вектори  і
і  утворюють кут
утворюють кут  . Обчислити модуль вектора
. Обчислити модуль вектора  якщо
якщо 
Розв’язання.Модуль вектора 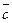 визначимо за формулою
визначимо за формулою  . Використовуючи властивості скалярного добутку, знаходимо
. Використовуючи властивості скалярного добутку, знаходимо 
Згідно означення скалярного добутку маємо:
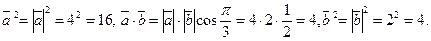 Отже,
Отже, 
Приклад 1.5. Дано координати вершин трикутника А(0;1), В(2;11), С(10;7). Методами аналітичної геометрії знайти:
а) загальні рівняння прямих АВ і АС, нормальні вектори та кутові коефіцієнти цих прямих;
б) рівняння прямої АВ у відрізках;
в) загальне рівняння прямої АК, яка містить медіану трикутника АВС;
г) загальне рівняння висоти СЕ та її довжину;
д) внутрішній кут  при вершині А трикутника АВС;
при вершині А трикутника АВС;
е) рівняння прямої, що проходить через точку В:
1. паралельно до прямої АС;
2. перпендикулярно до прямої АС;
є) координати центра ваги трикутника.
Зробити рисунок.
Розв’язання.Зробимо рисунок.

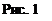
а) Підставивши в рівняння прямої, що проходить через дві дані точки координати точок А і В, отримаємо рівняння прямої АВ:
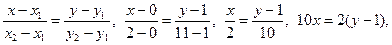
5х – у+ 1=0– загальне рівняння прямої АВ,  – нормальний вектор прямої.
– нормальний вектор прямої.
Розв’яжемо рівняння прямої АВ відносно змінної у: у=5х+1 – рівняння прямої з кутовим коефіцієнтом, де  =5.
=5.
Аналогічно знаходимо загальне рівняння прямої АС.
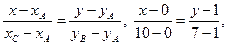

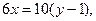
3х – 5у +5 =0 – загальне рівняння,  – нормальний вектор прямої.
– нормальний вектор прямої.
 – рівняння прямої АС з кутовим коефіцієнтом, де
– рівняння прямої АС з кутовим коефіцієнтом, де  .
.
б) Зведемо загальне рівняння прямої АВ до рівняння у відрізках. Для цього перенесемо вільний член заданого рівняння в праву частину рівності і поділимо на нього обидві частини рівняння. Отримаємо: 
З цього рівняння видно, що пряма відтинає на осях координат відрізки  і
і  , тобто, проходить через точки Д(-
, тобто, проходить через точки Д(-  ;0) та А(0;1).
;0) та А(0;1).
в) Знайдемо спочатку координати точки К, як середини відрізка ВС.

тобто, К(6;9).
Знайдемо рівняння медіани АК як рівняння прямої, що проходить через точки А і К:
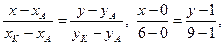 4х –3у +3=0.
4х –3у +3=0.
г) Оскільки нормальний вектор  прямої АВ буде напрямним до прямої СЕ, то, скориставшись канонічним рівнянням прямої, знайдемо рівняння висоти :
прямої АВ буде напрямним до прямої СЕ, то, скориставшись канонічним рівнянням прямої, знайдемо рівняння висоти :
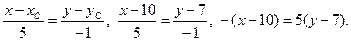
Звідки х +5у – 45=0 – шукане рівняння.
Довжину цієї висоти знайдемо як відстань від точки С до прямої АВ:
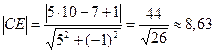 (лін. од.)
(лін. од.)
д) Внутрішній кут φ при вершині А заданого трикутника, знайдемо як кут між прямими АВ і АС.
Оскільки  ,
,  - нормальні вектори цих прямих,
- нормальні вектори цих прямих, 

Тоді 
е) 1. Запишемо рівняння в’язки прямих, що проходять через точку В(2;11): у – 11 =  ( х – 2). Оскільки шукана пряма паралельна до прямої АС (
( х – 2). Оскільки шукана пряма паралельна до прямої АС (  знайдено вище), то їх кутові коефіцієнти пов’язані співвідношенням
знайдено вище), то їх кутові коефіцієнти пов’язані співвідношенням  . Тоді рівняння прямої, що проходить через точку В і паралельна до прямої АС запишеться так:
. Тоді рівняння прямої, що проходить через точку В і паралельна до прямої АС запишеться так:
у – 11 =  (х – 2) або 3х – 5у +49 =0.
(х – 2) або 3х – 5у +49 =0.
2. Аналогічно до випадку 1 маємо у – 11 =  ( х – 2) – рівняння в’язки прямих, що проходять через точку В. Кутовий коефіцієнт шуканої прямої знайдемо з умови її перпендикулярності до прямої АС, тобто,
( х – 2) – рівняння в’язки прямих, що проходять через точку В. Кутовий коефіцієнт шуканої прямої знайдемо з умови її перпендикулярності до прямої АС, тобто,  Тоді у – 11 =
Тоді у – 11 = 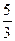 (х – 2) або 5х + 3у–43 =0 – рівняння прямої, що проходить через задану точку В перпендикулярно до прямої АС.
(х – 2) або 5х + 3у–43 =0 – рівняння прямої, що проходить через задану точку В перпендикулярно до прямої АС.
є) І спосіб. Координати точки М – центра ваги трикутника АВС, знайдемо за формулами:

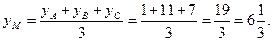
Шукана точка М(4;6  ).
).
ІІ спосіб. Координати центра ваги трикутника співпадають з точкою перетину його медіан. Оскільки медіани в точці перетину діляться у відношенні 2:1 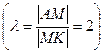 , то координати точки М – центра ваги трикутника, знайдемо за формулами:
, то координати точки М – центра ваги трикутника, знайдемо за формулами:


Отже, М(4;6  ).
).
Приклад 1.6. Скласти канонічне рівняння еліпса, якщо відстань між фокусами рівна 18, а велика піввісь – 12.
Розв’язання.За умовою задачі 2с=18, а=12. Із співвідношення b2=a2-c2 знаходимо b2=122-92=144-81=63.
Отже, рівняння еліпса має вигляд 
Приклад 1.7. Скласти рівняння гіперболи, якщо її дійсна піввісь дорівнює 8, а ексцентриситет  .
.
Розв’язання.За умовою задачі а=8,  . Оскільки
. Оскільки  то
то 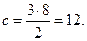 Із співвідношення b2=a2– c2 маємо b2=122– 82=144– 64=80.
Із співвідношення b2=a2– c2 маємо b2=122– 82=144– 64=80.
Отже, рівняння гіперболи 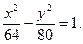
Приклад 1.8. Знайти координати центра, півосі та ексцентриситет еліпса, заданого рівнянням  .
.
Розв’язання.Згрупуємо доданки, які містять однакові змінні, і доповнимо отримані вирази до повних квадратів. Маємо:
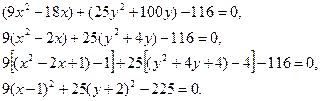
Звідси 
Центр еліпса знаходиться в точці С(1;-2), півосі а=5, b=3. Оскільки  , то ексцентриситет еліпса
, то ексцентриситет еліпса 
Приклад 1.9. Знайти координати вершини і значення параметра р параболи, заданої рівнянням  .
.
Розв’язання.Згрупуємо доданки із змінною y і виділимо повний квадрат. Маємо  або
або 
Координати вершин параболи знаходяться в точці А(-4;3). Параметр р знаходимо з умови  Вісь симетрії параболи паралельна до осі ОХ.
Вісь симетрії параболи паралельна до осі ОХ.
Приклад 1.10. Побудувати плоску фігуру, обмежену лініями  і
і  .
.
Розв’язання.Знайдемо координати точок перетину параболи і прямої, розв’язавши систему рівнянь:
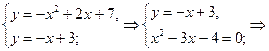 х1=-1, х2=4.
х1=-1, х2=4.
Отже, А(-1;4) і В(4;-1) – точки перетину ліній.
Побудуємо лінії та заштрихуємо фігуру Ф, яка обмежена зверху параболою, а знизу – прямою (рис.2).
 Для знаходження вершини параболи зведемо її рівняння до канонічного виду:
Для знаходження вершини параболи зведемо її рівняння до канонічного виду:


Отже, вершина параболи знаходиться в точці С(1;8), вітки направлені вниз, вісь симетрії х=1.
Завдання для самоконтролю
1. Розв’язати системи рівнянь:
а)  б)
б) 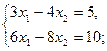 в)
в) 
г) 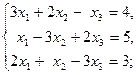 д)
д) 
е) 
2. Вектори  і
і 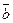 утворюють кут
утворюють кут  . Знаючи, що
. Знаючи, що  ,
,  обчислити:
обчислити:
а)  ; б)
; б) 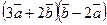 ; в)
; в)  ;
;
г)  .
.
3. Дано точки А(3;-1;0), В(2;1;1), С(3;0;-2). Знайти:
а) координати векторів  ,
, 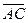 та їх модулі;
та їх модулі;
б) кут між векторами  і
і 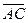 ;
;
в) 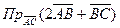 .
.
4. При якому значенні α вектори  =(2;0;α) і
=(2;0;α) і  =(3;4;2) перпендикулярні?
=(3;4;2) перпендикулярні?
5. Дано вершини трикутника А(4;3), В(-3;-3), С(2;7).Знайти:
а) рівняння прямих АВ і АС, нормальні вектори та кутові коефіцієнти цих прямих;
б) рівняння прямої АС у відрізках;
в) рівняння прямої АК, що містить медіану трикутника АВС;
г) рівняння висоти СЕ та її довжину;
д) внутрішній кут φ при вершині А;
е) рівняння прямої, що проходить через точку В:
1. перпендикулярно до прямої АС;
2. паралельно до прямої АС;
є) координати центра ваги трикутника.
Зробити рисунок.
6. Знайти рівняння кола, якщо кінці одного з його діаметрів знаходяться в точках А(3;9) і В(7;3).
7. Скласти канонічне рівняння еліпса, якщо його велика піввісь а=12, а ексцентриситет  =0,5.
=0,5.
8. Знайти півосі, координати фокусів і ексцентриситет еліпса  . Зробити рисунок.
. Зробити рисунок.
9. Скласти канонічне рівняння гіперболи, якщо її дійсна піввісь а=8, а ексцентриситет  =
=  .
.
10. Звести до канонічного виду рівняння гіперболи 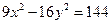 . Знайти координати її фокусів, ексцентриситет і рівняння асимптот. Зробити рисунок.
. Знайти координати її фокусів, ексцентриситет і рівняння асимптот. Зробити рисунок.
11. Визначити точки перетину прямої x+y– 3=0 і параболи 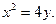
12. Встановити, яку криву задає рівняння (зробити рисунок):
а) 
б) 
в) 
г) 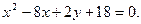
13. Побудувати плоску фігуру, обмежену лініями 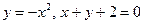 .
.
