Заступна схема мережі, вибір контурів та формування дерева графа ЕЕС
Для формування математичної моделі мережі необхідно побудувати схему заміщення, яка представляє собою сукупність схем заміщення окремих її елементів, з’єднаних між собою в тій же послідовності, що і в реальній схемі. При цьому схеми заміщення складаються на одну фазу з нейтраллю.
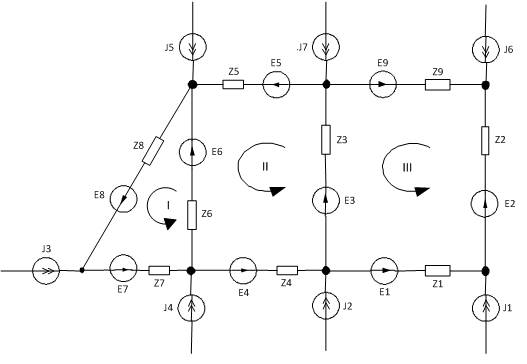 Таким чином, для схеми заміщення електричної системи, яка використовується для розрахунку встановлених режимів, представляє собою електричне коло. Це означає, що до схеми заміщення електричної системи можна застосовувати такі поняттєві характеристики електричних кіл, як вітка, вузол, контур. Як відомо, віткою називається ділянка кола, яка складається з послідовно з’єднаних ЕРС і опору (або тільки опору) і вздовж якої в будь-який заданий момент часу струм має одне і те ж саме значення. Вузол визначається як точка з’єднання двох і більше віток, а контур – як ділянка кола, утворена таким послідовним з’єднанням декількох віток, при якому початок першої вітки контура з’єднаний з кінцем останньої в одному вузлі. Згідно завдання схема буде мати вид показаний на рисунку 1.1
Таким чином, для схеми заміщення електричної системи, яка використовується для розрахунку встановлених режимів, представляє собою електричне коло. Це означає, що до схеми заміщення електричної системи можна застосовувати такі поняттєві характеристики електричних кіл, як вітка, вузол, контур. Як відомо, віткою називається ділянка кола, яка складається з послідовно з’єднаних ЕРС і опору (або тільки опору) і вздовж якої в будь-який заданий момент часу струм має одне і те ж саме значення. Вузол визначається як точка з’єднання двох і більше віток, а контур – як ділянка кола, утворена таким послідовним з’єднанням декількох віток, при якому початок першої вітки контура з’єднаний з кінцем останньої в одному вузлі. Згідно завдання схема буде мати вид показаний на рисунку 1.1
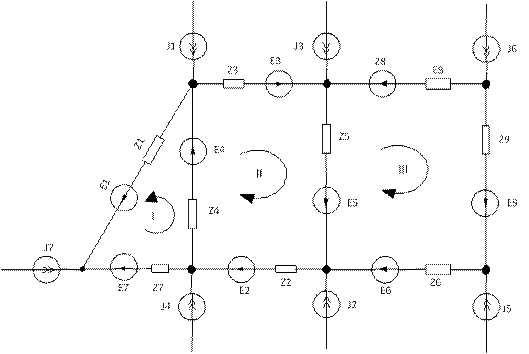
Рисунок 1.1 – Схема заміщення
Схема заміщення електричного кола (електричної мережі) може розглядатися як граф. Схема заміщення електричної мережі, як правило, є зв’язаним графом. Вона складається з віток (ребер), з’єднаних в вузли. Ці вітки утворюють ланцюги, які можуть бути замкнутими, і при цьому перетворюються в замкнуті контури. Всі величини, які характеризують стан віток (струми, напруги, ЕРС), мають певний напрям (без чого не може бути знайдений з достатньою повнотою робочий режим даної схеми). В зв’язку з цим доцільно кожній вітці схеми надати певний (довільно вибраний) напрям. Таким чином, схема заміщення мережі зазвичай є зв’язаним, направленим графом, ребрами якого є вітки, а вершинами – вузли.
Найменший зв’язаний підграф, який містить всю сукупність вершин графа, є його деревом. Такий підграф не містить контурів. Число віток, які входять в склад дерева, на одиницю менше числа вузлів всієї схеми.
Таку розімкнуту схема можна отримати шляхом виключення віток, які входять в незалежні замкнуті контури схеми. Кожен замкнутий контур схеми розмикається, якщо виключається одна з віток, які входять в нього. Якщо почергово розімкнути всі незалежні замкнуті контури, то залишиться розімкнута частина схеми – дерево. Та частина схеми, яка залишилась, називається хордами графа.
Одна і та ж схема може бути розділена на дерево і хорди по-різному.
Варіанти графів для даної мережі:
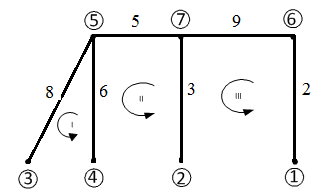
Рисунок 1.2 – Варіант 1 дерева графа
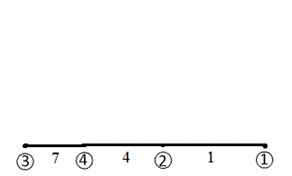
Рисунок 1.3 – Варіант 1 хорд графа
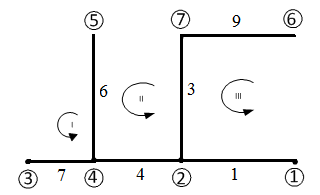
Рисунок 1.4 – Варіант 2 дерева графа
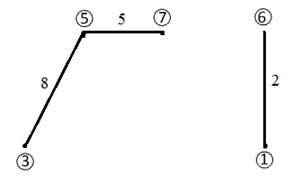
Рисунок 1.5 – Варіант 2 хорд графа
