Изменение кинетической энергии и работа равнодействующей

Кинетическая энергия

Пусть на покоящееся вначале тело массой m действуют постоянные силы, равнодействующую которых обозначим 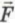(рис. 29.1).

Если перемещение тела равно , работа равнодействующей

A_рд = Fs. (1)

Индекс «рд» подчеркивает, что речь идет о работе равнодействующей всех приложенных к телу сил.

Дело в том, что мы будем использовать сейчас второй закон Ньютона, согласно которому модуль равнодействующей F связан с модулем ускорения тела а соотношением F = ma. Поэтому из формулы (1) следует:

A_рд = mas. (2)

При равноускоренном движении без начальной скорости (см. § 6):

s = v²/(2a). (3)

Подставим это выражение для s в формулу (2) и получим:

Aрд = (mv²)/2. (4)

В курсе физики основной школы вы уже познакомились с выражением, стоящим справа в формуле (4). Напомним, что
кинетическая энергия тела массой m, движущегося со скоростью , выражается формулой

E_k = (mv²)/2. (5)

(Мы рассматриваем тело как материальную точку.)

Итак, кинетическая энергия тела, движущегося с некоторой скоростью, равна работе, которую нужно совершить, чтобы разогнать покоившееся вначале тело до этой скорости.

? 1. Скорость тела увеличилась в 2 раза. Как изменилась его кинетическая энергия?

? 2. Кинетическая энергия тела уменьшилась в 2 раза. Как изменилась его скорость?

Изменение кинетической энергии и работа равнодействующей

Пусть теперь начальная скорость тела равна 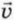₁, а направление равнодействующей 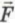по-прежнему совпадает с направлением начальной скорости (а тем самым и с направлением перемещения 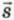). Обозначим конечную скорость тела 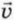₂.

? 3. Докажите, что в этом случае работа равнодействующей приложенных к телу сил равна изменению кинетической энергии:

A_рд = Fs = (mv₂²)/2 – (mv₁²)/2. (6)

Подсказка. Воспользуйтесь формулой s = (v₂² – v₁²)/(2a) (см. § 6).
Итак,
работа A_рд равнодействующей всех сил, приложенных к телу, равна изменению его кинетической энергии:

A_рд = E_k2 – E_k1. (7)

Это чрезвычайно полезное утверждение называют теоремой об изменении кинетической энергии. (В некоторых учебниках ее называют «теоремой о кинетической энергии». Мы используем более точное название (см. «Физическую энциклопедию»).) Как мы видели, она является следствием второго закона Ньютона. Поэтому применять ее можно во всех случаях, когда применим второй закон Ньютона:

· в любой инерциальной системе отсчета;

· для равнодействующей любых сил: природа этих сил (тяготения, упругости или трения) не существенна.

Мы доказали теорему об изменении кинетической энергии для случая, когда равнодействующая приложенных к телу сил постоянна и ее направление совпадает с направлением перемещения тела. Однако можно доказать, что она справедлива при любом угле между равнодействующей приложенных к телу сил и перемещением этого тела. Более того, равнодействующая может быть даже не постоянной, а переменной силой.

Благодаря этому теорему об изменении кинетической энергии можно с успехом применять, чтобы находить изменение кинетической энергии (а тем самым и изменение скорости) тела при перемещении по любой траектории. Для этого надо вычислить работу равнодействующей приложенных к телу сил.

Работа равнодействующей равна алгебраической сумме работ всех сил, действующих на тело. Поэтому чтобы найти работу равнодействующей, достаточно найти работу каждой силы при перемещении тела и сложить эти работы с учетом их знаков.

Рассмотрим несколько примеров.

Начнем с простых задач, а потом перейдем к задачам, которые просто решаются с помощью теоремы об изменении кинетической энергии, но которые вы не смогли бы решить непосредственным применением законов Ньютона.

? 4. На тело массой 2 кг действует сила 10 Н. В начальный момент скорость тела равна 5 м/с и ее направление совпадает с направлением силы. Тело переместилось на 5 м.
а) Чему равна работа силы?
б) Какова начальная кинетическая энергия тела?
в) Какова конечная кинетическая энергия тела?

? 5. На земле лежит камень массой 2 кг. К нему прикладывают направленную вертикально вверх силу , равную 30 Н.
а) Чему равна работа силы тяжести за промежуток времени, в течение которого камень подняли на 10 м?
б) Чему равна работа силы за то же время?
в) Чему равна работа равнодействующей сил, приложенных к камню, за то же время?
г) Какова конечная кинетическая энергия камня?
д) Какова конечная скорость камня?

? 6. Находящемуся на столе бруску массой 0,5 кг придали начальную скорость 2 м/с. До остановки брусок переместился по столу на 1 м.
а) Чему равно изменение кинетической энергии бруска за время движения по столу?
б) Чему равна работа равнодействующей всех сил, приложенных к бруску при движении по столу?
в) Чему равна работа силы тяжести?
г) Чему равна работа силы нормальной реакции?
д) Чему равна работа силы трения?
е) Чему равна сила трения?
ж) Каков коэффициент трения между бруском и столом?

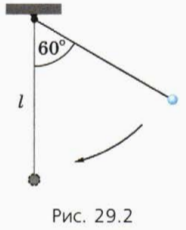
7. Шар массой m, висящий на нити длиной l, отклонили на 60º. Держа нить натянутой, шар отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 29.2)?
б) Чему равна работа действующей на шар силы натяжения нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?
г) Чему равна кинетическая энергия шара при прохождении положения равновесия?
д) Чему равна скорость шара в момент прохождения положения равновесия?

? 8. Шар массой m, укрепленный на пружине жесткостью k, может скользить без трения вдоль горизонтального стержня (рис. 29.3). Массой пружины можно пренебречь. В начальный момент скорость шара равна нулю, а пружина сжата и модуль ее деформации равен x.

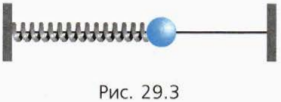
а) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия (в котором пружина не деформирована)?
б) Чему равна кинетическая энергия шара при прохождении положения равновесия?
в) С какой скоростью шар проходит положение равновесия?