Жазық фигура нүктелерінің жылдамдықтарын жылдамдықтардың лездік центрін пайдалану арқылы есептеу

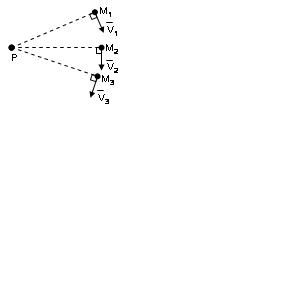
2.25-сурет

Жылдамдықтардың лездік центрі деп, берілген лездік уақыт t мезгілінде, жылдамдығы нөлге тең болатын жазық фигура жазықтығының бір нүктесін айтамыз.

Жазық фигура нүктелерінің жылдамдықтарын анықтаудың геометриялық әдісінің бір түрі, осы жазық фигураның лездік центрін

пайдалануға негізделген. Оны мына теорема арқылы айтуға болады.

3-ші теорема. Егер жазық фигураның қандайда бір нүктесінің жылдамдығы берілсе және оның екінші бір нүктесінің жылдамдығының бағыты ғана белгілі болса, онда бұл фигура жазықтығының кез келген нүктелерінің жылдамдықтарын, жылдамдықтардың лездік центрі арқылы табуға болады.

Жазық фигура (S) –тің бір нүктесі М₁ – дің жылдамдық векторы ₁ берілсін және оның екінші бір нүктесі М₂ – нің жылдамдық векторы жататын түзу бағыты белгілі болсын дейік (2.26-сурет).

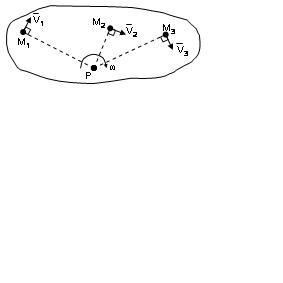
2.26-сурет

М₁ жене М₂ нүктелерінің жылдамдықтарының берілген бағыттары арқылы лездік центр Р-ның орнын табамыз.

Олардың жылдамдықтары лездік радиустар РМ₁, РМ₂, РМ₃ ұзындықтарына пропорционал болып келеді:

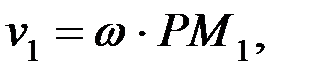
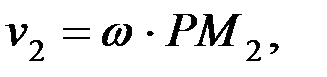
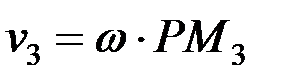
мұндағы ω жазық фигураның Р центрді айналысының лездік бұрыштық жылдамдығы. Оны соңғы үш теңдіктердің біріншісінен табамыз.

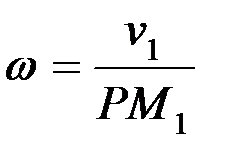
Осыдан қалған екі теңдіктердегі орнына қойсақ

.

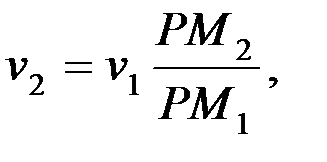
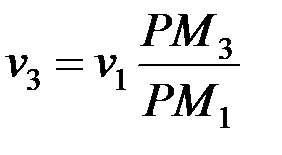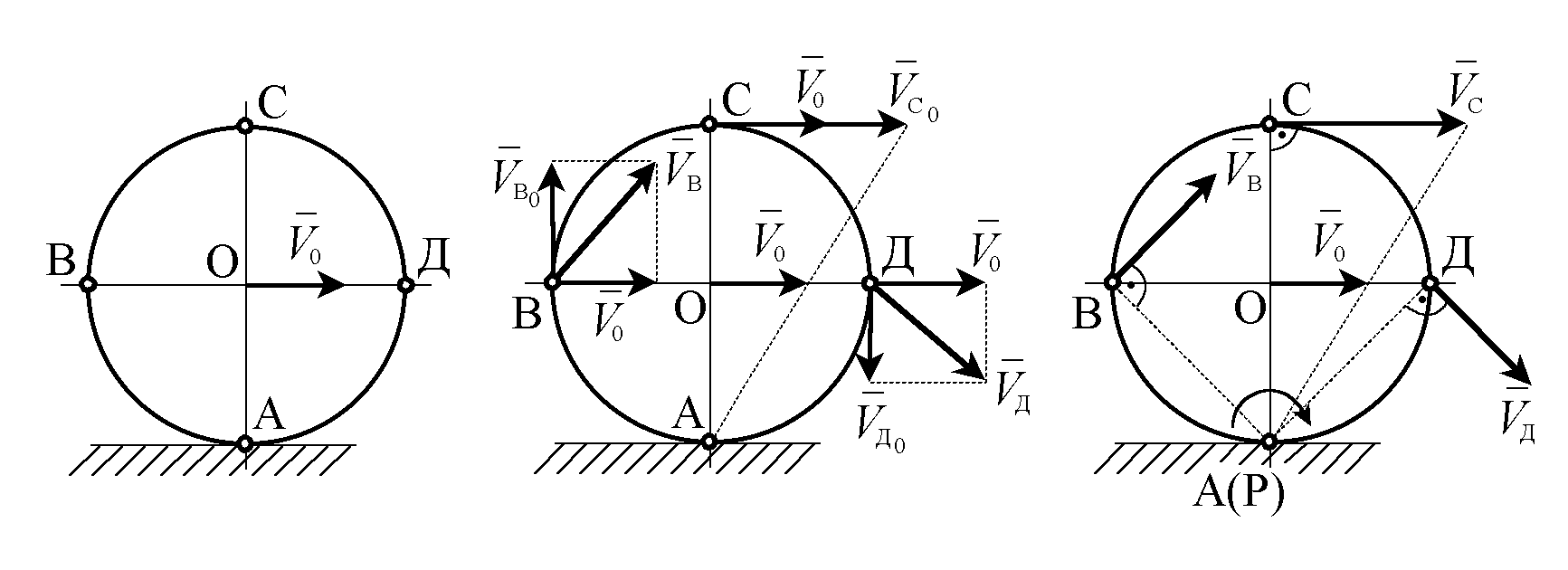
Мысал: Радиусы R = 0.5м түзу рельс бойымен сырғанамай дөңгелеп қозғалады; оның центінің жылдамдығы тұрақты және v₀ = 10 м/с-ке тең.

Дөңгелектің горизонталь және вертикаль диаметрлерінің соңғы A, B, C, D нүктелерінің жылдамдықтарын және бұрыштық жылдамдығын анықтау керек.

1.27-сурет

Шешуі:І-тәсіл: (жылдамдықтардың таралу формулаларын пайдалану).

Полюс ретінде О центрін қабылдаймыз (1.27-сурет). Онда дөңгелектің кез келген нүктесінің жылдамдығы полюс жылдамдығы мен полюсті айнала қозғалыс жылдамдығының геометриялық қосындысына тең, мысалы 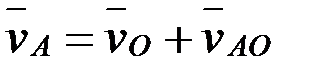. Дөңгелек сырғанамай дөңгелеп қозғалатын болғандықтан дөңгелек пен рельстің жанасушы А нүктесінің жылдамдығы нөлге тең 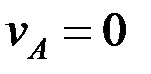, яғни А нүктесі лездік жылдамдық центрі болып табылады. Бұл нүктеде полюсті айнала қозғалыс жылдамдығы 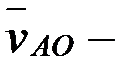мен полюс жылдамдығы 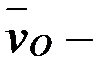ның шамалары тең, ал бағыттары қарама-қарсы, яғни 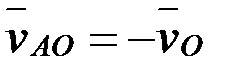. A, B, C, D нүктелерінен полюске дейінгі ара қашықтықтары тең. Сондықтан, нүктелердің полюсті айнала қозғалыс жылдамдықтары өз-ара тең, яғни .

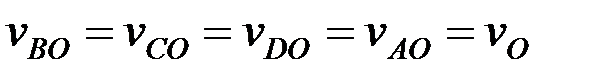Әрбір нүктеден полюс жылдамдығы 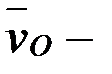ны және дөңгелектің радиусына перпендикуляр полюсті айнала қозғалыс жылдамдығын тұрғызып табатынымыз:

, ,

.

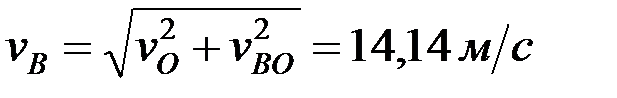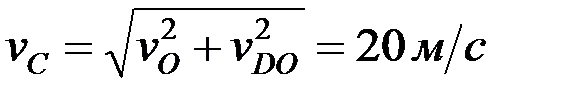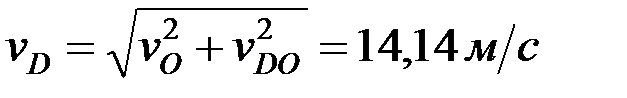Бұрыштық жылдамдығы:

.

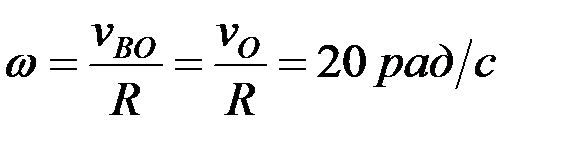II-тәсіл: (жылдамдықтар лездік центрін пайдалану):

Дөңгелектің жылдамдықтар лездік центрі A–ны полюс ретінде қабылдаймыз. Онда дөңгелектің барлық нүктелерінің жылдамдықтары жылдамдықтар лездік центрін айнала қозғалыс жылдамдықтары болады. Барлық нүктелердің жылдамдықтарының шамалары мынадай қатынастармен анықталады:

, ,

,

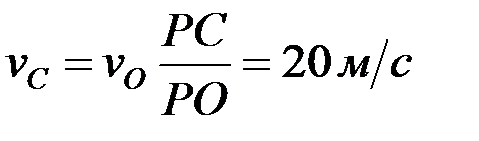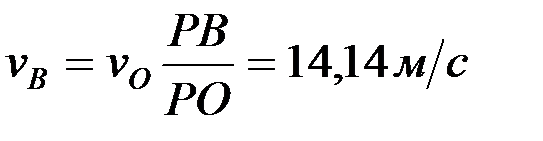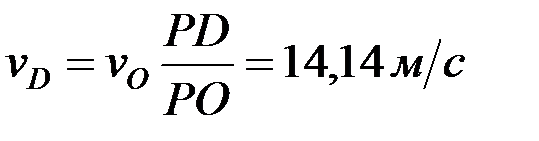мұндағы .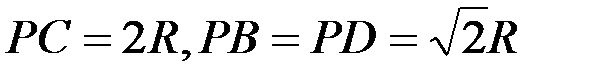

Бұрыштық жылдамдығы мынадай қатынаспен анықталады:

.
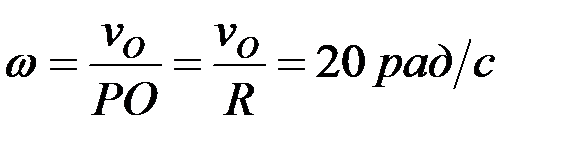