Свойства сходящихся последовательностей
31.
Определение.
Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x1,x2,...xn
Числа x1,x2,...,xn — называются элементами последовательности, символ xn — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {xn}.
Свойства ограниченных последовательностей
- Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.
- Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.
- Ограниченная последовательность имеет по крайней мере одну предельную точку.
- У ограниченной последовательности существуют верхний и нижний пределы.
- Для любого наперёд взятого положительного числа ε все элементы ограниченной числовой последовательности
 , начиная с некоторого номера, зависящего от ε, лежат внутри интервала
, начиная с некоторого номера, зависящего от ε, лежат внутри интервала 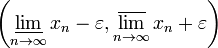 .
. - Если за пределами интервала
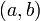 лежит лишь конечное число элементов ограниченной числовой последовательности
лежит лишь конечное число элементов ограниченной числовой последовательности  , то интервал
, то интервал  содержится в интервале
содержится в интервале 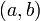 .
. - Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Определение. Арифметические действия.
Пусть даны последовательности {xn} и {yn}.
- Произведением последовательности {хn} на число m назовем последовательность m·x1, m·x2, …, m·xn, ….
- Суммой данных последовательностей назовем последовательность x1 + y1, x2 + y2, …, xn + yn, ….
- Разностью – последовательность x1 − y1, x2− y2, …, xn− yn, …,
- Произведением — последовательность x1·y1, x2·y2, … xn·yn,…
- Частным — последовательность
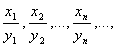 если все члены последовательности {yn} отличны от нуля.
если все члены последовательности {yn} отличны от нуля.
Указанные действия над последовательностями символически записываются так:
- – m·{ xn} = {m· xn}
- – { xn} + { yn} = { xn + yn}
- – { xn} - { yn} = { xn - yn}
- – { xn} · { yn} = { xn · yn}
- –
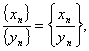 если yn ≠ 0.
если yn ≠ 0.
Т. Лемма
Если 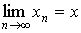 и
и  , то
, то 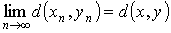 .
.
Определение.
Последовательность, имеющая предел, называется сходящейся. Если последовательность {xn} сходится и имеет своим пределом число a, то символически это записывается так:
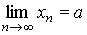 или xn→ a при n → ∞
или xn→ a при n → ∞
Последовательность, не являющаяся сходящейся, называется расходящейся.
Последовательность (xn) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство |xn - a| < ε.
Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве.
Последовательностью имеющий конечный пределназывают сходящимися. В противном случае последовательность называют расходящимися. Среди них есть последовательности, которые расходятся в бесконечность. О них мы говорим, что они имеют бесконечный предел.
Свойства сходящихся последовательностей
- Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
- Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
- Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.
- Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
- Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
- Если последовательность (xn) сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность (1 / xn), которая является ограниченной.
- Сумма сходящихся последовательностей также является сходящейся последовательностью.
- Разность сходящихся последовательностей также является сходящейся последовательностью.
- Произведение сходящихся последовательностей также является сходящейся последовательностью.
- Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
- Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
- Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
- Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
- Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.
- Любую сходящуюся последовательность (xn) можно представить в виде (xn) = (a + αn), где a — предел последовательности (xn), а αn — некоторая бесконечно малая последовательность.
- Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).
Определение.
Наименьшее среди всех чисел, ограничивающих сверху числовое множество Е 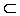 R, называется его верхней гранью и обозначается β = sup E, то есть
R, называется его верхней гранью и обозначается β = sup E, то есть
-
 x
x  E: x ≤ β,
E: x ≤ β, -
 ε > 0
ε > 0 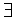 x
x  E: x > β - ε.
E: x > β - ε.
Наибольшее среди всех чисел, ограничивающих числовое множество Е 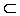 R, называется его нижней гранью и обозначается α = inf E, то есть
R, называется его нижней гранью и обозначается α = inf E, то есть
-
 x
x  E: x ≥ α,
E: x ≥ α, -
 ε > 0
ε > 0 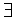 x
x  E: x < α + ε.
E: x < α + ε.
Т. Больцано – Вейерштрасса
Монотонно возрастающая (убывающая) ограниченная сверху (снизу) последовательность должна иметь предел.
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
