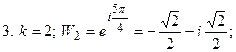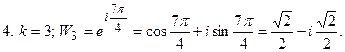Действия над комплексными числами

На множестве комплексных чисел определены те же действия, что и на множестве действительных чисел. Пусть

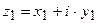и

а) Сумма и разность двух комплексных чисел определяется следующим образом:

т.е. при сложении комплексных чисел их действительные и мнимые части складываются, а при вычитании вычитаются.

Модуль суммы комплексных чисел меньше либо равен сумме модулей этих чисел:

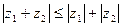
Доказательство: принимая во внимание, что модуль комплексного числа равен длине соответствующего этому числу вектора и что одна сторона треугольника короче суммы двух других сторон, то 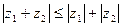. Причем знак будет иметь место лишь в том случае, когда векторы соответствующих комплексных чисел z₁ и z₂ одинаково направлены, т. е. когда аргументы этих чисел равны или отличаются на кратное 2 .

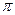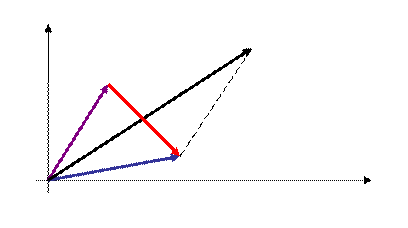
1) фиолетовой линией обозначено z₂ ;

2) синей линией обозначено z₁ ;

3) красной линией обозначена разность z₁ - z₂ ;

4) черной линией обозначена сумма z₁ + z₂ ;

- это выполняется когда направления противоположны.

б) Произведение двух комплексных чисел получается по правилу умножения многочленов, учитывая, что i² = -1:

Если комплексные числа заданы в тригонометрической форме:

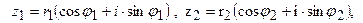(6)

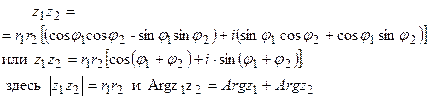
Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей: .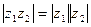

Доказать самостоятельно.

В показательной форме:

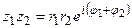
в) Деление комплексных чисел вводится как операция, обратная умножению:

В алгебраической форме:

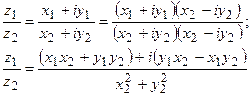
Пример: Вычислить:

Пусть числа z₁ и z₂ заданы в тригонометрической форме (6). Найдём модуль и аргумент частного. По определению:

и .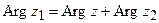

Отсюда: 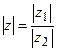и .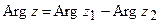

Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.

или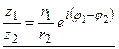

г) Возведение комплексных чисел в натуральную степень.

Целая положительная степень комплексного числа определяется так же, как и действительного: .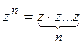

Например:

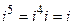и т.д. В общем случае:

.

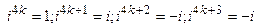Пусть число z задано в тригонометрической форме:

Тогда .

Отсюда:

.

Рис. 4.

В показательной форме:

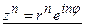
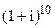Пример. Вычислить . Запишем число z=1+i в тригонометрическом виде. Здесь = ,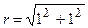

tg =1; ; z = (рис. 4).

д) Извлечение корня.

Корнем n-ой степени из комплексного числа z называется такое число w (w= ), что wⁿ=z.

Пусть числа z и w представлены в тригонометрической форме:

и

Найдём ρ иq. Так как

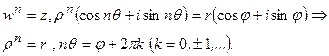
Поэтому: ρ= - арифметическое значение корня из положительного числа r, а q= 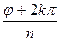(k= ). Т.о.

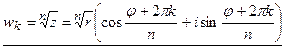или

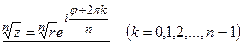
Значение q_к, дающие существенно различные значения корня n-ой степени из z соответствуют только n значениям k (0,1,2,…n-1). Остальным целым k соответствуют значения q_k, отличающиеся от одного из указанных значений на величину, кратную 2π.

Проверить, например, что w_n=w₀ !

Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из этих формул. Из формул вытекает, что все значения корня лежат на окружности радиуса ρ= и делят окружность на n равных частей.

Пример 1: Вычислить 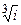. Запишем число в тригонометрической форме:

Рис.5.

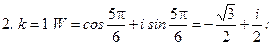
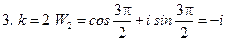
Пример 2: Вычислить . Запишем число в показательной форме:

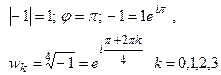
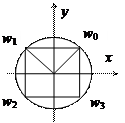
Рис. 6.