Существенное значение для работы системы АПЧ при больших расстойках имеет также форма скатов детекторной характеристики. 3 страница

Можно чисто качественно описать поведение системы ФАПЧ при воздействии шума \ (t). При большом отношении сигнал/шум разность фаз Ф (/) будет разбросана в окрестности начальной точки устойчивого равновесия фо (см. рис. 10.3). При сравнимом отношении сигнал/шум шумовое воздействие может вывести систему ФАПЧ из области начального устойчивого равновесия ф₀ и перебросить в соседние состояния равновесия ф±!, ф±₂ и т. д., т. е. в системе ФАПЧ происходят перескоки фазы на ± 2nk, возрастающие с течением времени.

Определим нестационарную функцию распределения р (ф, /), воспользовавшись диффузионным уравнением Фоккера — Планка — Колма-горова [см. (11.45)1:

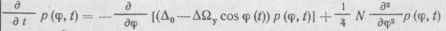
(10.21)

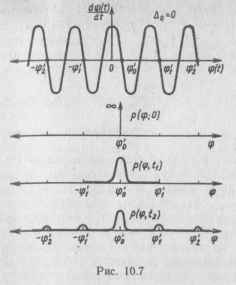
где Д„ —■ Ай_у cos ф (t) = а (ф) — коэффициент сноса; N12 = Ь — коэффициент диффузии.

Наибольшее значение имеет ста-

ционарное распределение р (ср) = = lim р (ср, t). Оно соответствует в

(10.21) условию р (ф, t) — 0,

и, следовательно, дифференциальное уравнение в частных производных превращается в обыкновенное. Обозначив а = 4Д„/Л\ В = 4ДЙ_У/Л^/, получим

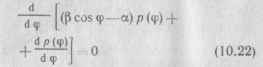
Проинтегрировав по ф, найдем решение

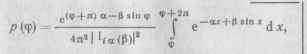
где /,-„ — функция Бесселя мнимого индекса и мнимого аргумента.

Решение этого интеграла можно получить через известные функции только для частного случая, когда а= Д_о=0, т. е. когда начальная расстройка между ГС и ПГ отсутствует и задача ФАПЧ состоит только в слежении за фазой. При этом условии

(10.23)

где /₀ (В) — функция Бесселя нулевого порядка мнимого аргумента.

Заметим, что коэффициент В пропорционален отношению сигнал/шум в полосе системы, так как AQ_y ~ ~ U_rU_c [см. (10.14)].

При малом отношении сигнал/шум (Р С 1) функция ехр (— В sin ср) да да 1„ (В) да 1. Тогда

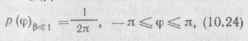
т. е. закон распределения р (ф) равновероятный.

При большом отношении сигнал/ шум "(В > 1) вначале надо разложить в ряд функцию sin ф вокруг установившегося значения разности фаз ГС и ПГ ф₀ = — я/2: sin (ф — — л/2) да 1 - ф²/2 при ф« 1. Затем

следует воспользоваться асимптотическим приближением I„ (В)р», аз да ехр В/К2лВ.Подстановка этих значений в (10.23) дает выражение для нормальной плотности вероятности:

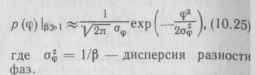
На рис. 10.8 приведены плотности вероятности разности фаз при Д₀ ==0 и различных значениях В, которые пропорциональны отношению сигнал/шум. Видно, что функция р (ф) изменяется от равновероятной (В—-0)

до нормальной (В > 1), а в пределе (Р—>-оо) стремится к б-образной. При этом всегда среднее значение <ф> = — л/2, а дисперсия о£ изменяется в зависимости от 6.

Отметим, что при наличии начальной расстройки по частоте Д„ ф 0 плотности вероятности р (ф) становятся асимметричными и, следовательно, средняя фаза смещается относительно ф = л/2. Графики изменения среднего значения <Ф> и среднеквадратического отклонения а_ф разности фаз в зависимости от отношения Д„/Дй_у приведены на рис. 10.9. С увеличением начальной расстройки Д₀ значения <ф> и о_щ возрастают, причем при Д„ -»-

ДО_у рост среднего значения замедляется, а рост дисперсии, наоборот, убыстряется.

Статистические характеристики ФАПЧ с реальными ФНЧ находят на основе их дифференциальных уравнений и по методике, описанной выше для ФАПЧ с идеальным фильтром.

Перейдем к представлению системы ФАПЧ в виде моделей. Рассмотрим модель, основанную на условии обеспечения синхронизма работы системы.

Используя формулу (10.6) для напряжения на выходе ФД, найдем напряжение на выходе ФНЧ:

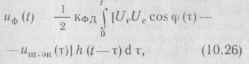
где "ш-эк(0 = U_ra_m (t)cosy (t)+ + ^с/г'^,ш(0 sin ф (/) — эквивалентный шум, представляющий собой нормальный процесс с равномерным энергетическим спектром NJ2 на низких частотах, ширина которого гораздо больше полосы частот, пропускаемых системой ФАПЧ; h (t) — импульсная переходная функция ФНЧ.

При отключении управляющего сигнала и_ф (/) от ПГ генератор выдает гармонический сигнал постоянной

частоты <о_го. После же подключения ПГ согласно (10.12) его частота

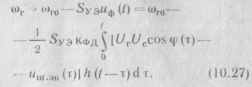
Чтобы не повторять постоянно начальную частоту (о_го, определим фазы ГС и ПГ по отношению к частоте

пг (о,.₀: ф, (/) ф,. ф,(0

ф,. (/) - - со_гиЛ Тогда формулу (10.27) можно привести к виду

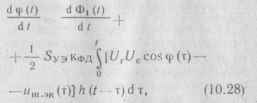
где ф(/) =Ф_х(/)-Ф₄(0.

Выражению (10.28) соответствует модель системы ФАПЧ в режиме синхронизма, изображенная на рис. 10.10. Фазовый детектор, который ранее представлялся как идеальный перемножитель двух напряжений, теперь формирует косинусоидальную функцию фазовой ошибки и, следовательно, представляется в виде двух последовательных функциональных блоков: вычитающей схемы и схемы формирования косинусоидальной нелинейности. Перестраиваемый генератор заменяется на интегратор, а это означает, что фаза выходного сигнала ПГ пропорциональна интегралу управляющего сигнала и_ф \t). ФНЧ заменяется звеном с передаточной функцией К_ФН (р). Влияние эквивалентного входного шума "ш-8к(0 учитывается непосредственным включением генератора шума в синхронную модель следящей системы уже после косинусоидальной нелинейности.

Рассмотрим теперь линейную модель системы ФАПЧ. Если считать, что динамическая фазовая ошибка мала, т. е. |ф (/)| < ' рад, то можно воспользоваться разложением функции cos ф (/) в (10.28) вокруг устой-

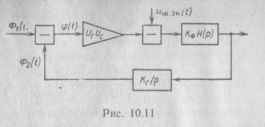
Рис. 10.11

чивого значения разности фаз фо = я/2 (см. рис. 10.3): cos (ф + я/2)-= — sin ф, а затем воспользоваться приближением

cos _чф-|- я/2) - - — siny « — ф. (10.29)

Система ФАПЧ в этом случае близка к захвату фазы, а косинусо-идальную нелинейность, показанную на рис. 10.10, можно не рассматривать. При этом работа системы ФАПЧ описывается линейным уравнением, которое получается при подстановке (10.29) в (10.28):

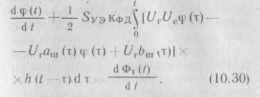
При использовании такого приближения схему, изображенную на рис. 10.10, можно заменить схемой линеаризированной модели системы ФАПЧ (рис. 10.11).

§ 10.4. Использование

системы ФАПЧ

в задачах радиоприема

Система ФАПЧ широко используется в суиергетеродинных приемниках для стабилизации частоты преобразованного сигнала ^юп |©_с (=F) ю._г| при изменениях частоты входного сигнала со_с или гетеродина «о,, из-за дестабилизирующих факторов. В результате реализуется' более узкая полоса пропуска-пня линейной части приемника, что имеет особо важное значение при высоких требованиях к чувствительности приемников лиана юна СВЧ.

Структурная схема приемника с системой ФАПЧ для этого случая приведена на рис. 10.12. На один вход ФД подводится выходной сигнал с УПЧ на преобразованной частоте to,,, а на второй вход — сигнал от эталонного гетеродина (ЭГ), имеющего частоту «эр,равную номинальному значению преобразованной частоты о)_п0. На выходе ФД вырабатывается сигнал ошибки в канале управления гетеродина Г, состоящем из фильтра нижних частот ФНЧ, усилителя постоянного тока УПТ и управляющего элемента УЭ для регулирования частоты гетеродина.

Назначение ФНЧ было обсуждено в § 10.1, 10.2, а УПТ служит для согласования максимального управляющего напряжения с максимальным размахом управляемой реактивности УЭ. Управляемые элементы могут быть электронными и электронно-механическими. Первые выполняются на полупроводниковых управляемых емкостях — варикапах, реактивных транзисторах, полевых диодах и др. Вторые представляют собой малогабаритные электродвигатели, вращающие оси переменных конденсаторов или перемещающие сердечник индуктивности. Основные требования к УЭ линейность и необходимая крутизна Sv3 дсо_г/дыфд.

Гетеродин является по существу частотным модулятором. Единственное требование, предъявляемое к гетеродину в системе ФАПЧ,— строгая линейная зависимость отклонения частоты генератора от управляющего напряжения в заданной полосе частот.

Кроме стабилизации преобразованной частоты система ФАПЧ ис-

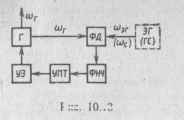
Рис. 10.13

пользуется для стабилизации только частоты гетеродина (рис. 10.13). При этом контур управления замыкается через цепь Г — ФД. Система ФАПЧ осуществляет подстройку частоты гетеродина Г под частоту эталонного генератора ЭГ. Сигнал ошибки при этом формируется в результате отклонения частоты гетеродина от частоты ЭГ. Очевидно, если эту систему применить для стабилизации преобразованной частоты, т. е. включить выход гетеродина Г на вход смесителя, то нестабильности частоты входного сигнала не будут компенсироваться.

Систему, изображенную на рис. 10.13, можно преобразовать в следящий фильтр, если на ФД вместо сигнала эталонного генератора подать входной сигнал с частотой ы_с. Тогда управляющее напряжение, формируемое ФД, будет определяться разностью частот входного сигнала co_t. и гетеродина со_г. Под воздействием этого напряжения частота гетеродина изменяется в соответствии с изменением частоты входного сигнала и система ФАПЧ обеспечивает слежение за этой частотой.

Если начальная расстройка по частоте А₀ входного сигнала и гете-

родина намного больше полосы захвата АИ₃ системы ФАПЧ, то для построения следящего фильтра целесообразно применить комбинацию параллельного соединения двух систем: ЧАПЧ и ФАПЧ (рис. 10.14).

Широкополосная система ЧАПЧ, использующая широкополосный фильтр (ШФ) и ЧД в качестве чувствительного элемента, обеспечивает необходимую полосу захвата сигнала и осуществляет слежение за частотой входного сигнала с некоторой ошибкой. Максимальная ошибка, слежения системы ЧАПЧ должна находиться в пределах полосы удержания AQ_y системы ФАПЧ. Как только частота гетеродина подстроится настолько близко к частоте сигнала, пропускаемого узкополосным фильтром (УФ), что сигнал ошибки войдет в полосу захвата системы ФАПЧ, последняя начнет функционировать. Гетеродин при работающей системе ФАПЧ точно следит за медленно изменяющейся частотой входного сигнала.

Узкая шумовая полоса системы ФАПЧ, достигающая десятков и даже единиц герц, позволяет получить большое отношение сигнал/шум на выходе. Однако для этого требуется, чтобы в момент включения системы ФАПЧ широкополосная система ЧАПЧ отключалась и вновь включалась только при поиске сигнала или его потере системой ФАПЧ.

Подобные комбинированные следящие фильтры широко применяют для измерения доплеровской частоты принятого сигнала, в устройствах формирования когерентных по частоте сигналов в оптимальных (квазиоптимальных) приемниках, каналах синхронизации радиотелеметрических систем, когерентных радиолиниях связи для получения опорного сигнала и в других приложениях.

В панорамных приемниках, обнаруживающих и оценивающих частоту принятого сигнала в широком диапазоне частот, система ФАПЧ может использоваться в устройствах автоматического поиска частоты

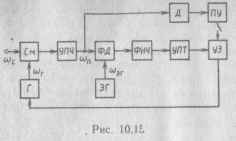
. Рис. 10.15

(рис. 10.15). Поисковое устройство (ПУ), представляющее собой генератор гармонических или пилообразных колебаний, подает напряжения на УЭ, изменяя частоту сигнала гетеродина Г, подаваемого на смеситель См, по соответствующим законам. На входе УПЧ выделяется напряжение преобразованной частоты со_п, подаваемое на ФД. Когда эта частота окажется близкой к частоте эталонного генератора, наступит режим захвата, система ФАПЧ будет следить за частотой входного сигнала и наступит режим следящего фильтра, при котором информация о частоте входного сигнала снимается с гетеродина.

Режим поиска и слежения следующий: во время поиска система ФАПЧ разомкнута и управляет поиском сигнала с выхода детектора Д, а в режиме слежения — система поиска (ПУ) отключается.

Использование системы ФАПЧ как устройства демодуляторов ФМ-ЧМ-и АМ-сигналов рассматривается в разд. 3.

§ 10.5. Цифровые системы ФАПЧ

В связи с развитием цифровых методов передачи и обработки информации широкое распространение получили цифровые системы ФАПЧ. Обобщенная структурная схема цифровой системы в принципе подобна аналоговой (см. рис. 10.1) с той лишь разницей, что каждое устройство является цифровым. На вход цифровой системы ФАПЧ (ЦФАПЧ) поступает периодический сигнал, который формируется устройством преобразования к виду, удобному для работы

цифрового фазового детектора (ЦФД) На второй вход ЦФД поступает сиг нал от цифрового перестраиваемого генератора (ЦПГ), в результате чеп на выходе ЦФД вырабатывается кс довая комбинация, соответствующа: разности фаз обоих входных сигналов В цифровом фильтре (ЦФНЧ) кодо вая комбинация подвергается фильт рации по определенному алгоритму Цифровой управляющий элемен' (ЦУЭ) вырабатывает управляющее на пряжение, которое в зависимости о входной кодовой комбинации произ водит дискретную коррекцию фазь или частоты ЦПГ.

Рассмотрим принцип действш ЦФАПЧ, где управление частотен ЦПГ осуществляется изменением фа зы некоторого опорного напряженж с помощью устройства «добавления — вычитания» (УДВ) импульсов опор ного генератора (ОГ). Структурна; схема подобной ЦФАПЧ показана н; рис. 10.16. Пусть на вход системы по ступает гармонический сигнал, кото рый формирующим устройством (ФУ преобразуется в последовательное™ коротких импульсов с частотой следо вания /о = 1/Т₀ (рис. 10.17, а). Для работы ЦФД требуется в общем слу чае четыре входа (входы / — IV) у два выхода (выходы /, //). На вхо; / поступает последовательность сигнальных импульсов, а на входы //, III с выхода делителя частоты (ДЧ) подаются две сдвинутые на 180° относительно друг друга импульсные последовательности типа меандр с частотой /_м = /о (рис. 10.17, б, в).

В зависимости от фазового рассогласования сигнальной импульсной

последовательности (вход /) с меандром (входы //, ///) вырабатывается строб ошибки длительностью Т_СтР (рис. 10.17, г), который заполняется вспомогательной импульсной последовательностью частоты /_в (рис. 10.17, д), когерентной частоте /₀ (вход IV). Таким образом, за длительность строба вырабатывается определенное число вспомогательной импульсной последовательности частоты /_в, поступающей на выход / ЦФД (рис. 10.17, е). Количество импульсов на выходе / и является кодовой комбинацией, характеризующей фазовое рассогласование входных колебаний.

Отметим, что если импульсы входа / приходятся на положительную полуволну меандра входа //, то кодовая комбинация снимается с выхода /, а на выходе // она отсутствует (рис. 10.17, ж). Если же импульсы входа / приходятся на положительную полуволну меандра входа ///, то кодовая комбинация снимается с выхода //, а на выходе / ее нет.

Число импульсов в кодовой комбинации зависит от соотношения частот /„ и /_в, а также от фазового рассог-

ласования ф \п\ в момент времени t_n = пТ₀ (п — 0, 1. 2, ...) входных сигналов. При равенстве частот импульсных последовательностей /„ = /"„ нормированная характеристика ЦФД/^?{ф[«1} является релейной, т. е. двухуровневой: — 1,1 (рис. 10.18, а), а при /_п >/„ многоуровневой (рис. 10.18, б).

ЦФНЧ выполняет обычную операцию интегрирующего или пропорционально-интегрирующего звена.

В бесфильтровой системе ЦФАПЧ при условии равенства частот входной и вспомогательной импульсных последовательностей (/„ = /_в) на вход УДВ за период регулирования в зависимости от разности фаз сравниваемых сигналов поступает один импульс коррекции — «опережения» (выход /) или «отставания» (выход //). Одновременно на УДВ от опорного генератора подается периодическая последовательность импульсов с частотой for — Df_n (рис. 10.19, а), где D > 1 — коэффициент деления делителя частоты, выбираемый из условия целесообразного дискрета фазовой коррекции. При добавлении

(рис. 10.19, б) или вычитании (рис. 10.19, г) одного импульса коррекции с выходов ЦФД соответственно изменяются длительности импульсов меандра (рис. 10.19, в, д) на величину ±Д7 — Тог. что соответствует фазовому сдвигу сигнала с выхода ДЧ на величину ±Аср = = 2n/D.

В отсутствие импульсов коррекции от ЦФД длительности полуволн меандра одинаковые. Таким образом,

функцию ЦПГ с управляющим з-j ментом выполняют ОГ, УДВ и Д

Если в начале работы ЦФАГ имелась частотная расстройка меж входным сигналом и меандром (/₀ Ф /_м), то будет наблюдаться нерехг ный процесс, по истечении которс средняя частота меандра станет равн частоте входного сигнала, а их ту венные значения могут отличатьс

Отметим, что существуют разлт ные модификации цифровых и аг лого-цифровых систем ФАПЧ [21

Основы

Статистической

Теории

Радиоприема

И структуры

Приемных

Устройств

ГЛАВА 11

СТАТИСТИЧЕСКИЙ СТРУКТУРНЫЙ СИНТЕЗ ОПТИМАЛЬНЫХ РАДИОПРИЕМНЫХ УСТРОЙСТВ

§ 11.1. Радиоприем

как статистическая задача

Структурный синтез радиоприемных устройств. В современных условиях радиоприемные устройства (РПУ), как правило, работают в сложной помеховой обстановке 1131. Поэтому обеспечение помехозащиты РПУ от различных видов помех естественного и искусственного происхождения является важной задачей.

Структурный синтез оптимальных РПУ в условиях помех заданного типа является одной из радикальных мер помехозащиты и изучается в статистической теории радиоприема [30]. Ниже рассматривается синтез в условиях воздействия на РПУ лишь аддитивных широкополосных шумовых помех («белого шума») гауссового или марковского типа.

Основная проблема оптимального приема состоит в наилучшем (в рамках заданного критерия оптимальности) решении поставленной перед радио-

приемным устройством задачи. При структурном синтезе оптимального РПУ возникает типичная статистическая задача: по заданным исходным (априорным) данным о статистических свойствах сообщений, сигналов, помех, радиоканалов и их функционального взаимодействия, при выбранном критерии оптимальности и типе решаемой в РПУ задачи найти оптимальные алгоритмы обработки информации. Наилучшими являются оптимальные радиоприемные устройства, синтезированные в условиях полной априорной определенности.. Априорная неопределенность снижает качество оптимального приема и требует специальных методов ее устранения.

Современная статистическая теория оптимального приема едина [30] для РПУ любых информационных радиосистем передачи информации, радиолокационных, радионавигационных и др. Она основана на математической статистике и теории статистических решений.

Виды оптимального приема. При

пространственно-временном приеме объектом наблюдения является поле смеси- сигнала и шума: Е_£ (/, г)= == Е_с(г, г, к) + Е_ш (t, г),принимаемое антенным устройством в некотором ограниченном объеме пространства г £ V и времени t £ Т. На основе обработки этого поля РПУ выносит некоторое решение D — D(?\.), как-то связанное с полезной информацией к.

При временном приеме объектом наблюдения, на основе которого выносится нужное решение D, является процесс

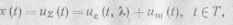
(11.1)

представляющий собой напряжение смеси сигнала и шума на выходе ан-тенно-фидерного устройства (АФУ) заданной конфигурации.

В теории оптимального приема радиоприемное устройство, состоящее из оптимального приемника и решающего устройства, с помощью решающего правила ф₀ (D/x(r)) на основе обработки процесса (11.1) выносит нужное решение D. При дискретной обработке наблюдаемый процесс (11.1) квантуется по времени (с шагом At = = Т/т) и заменяется векторной выборкой X — [х_л..... X) = х (tj

I At)..... х„,\.

Оптимальные радиоприемные устройства различного назначения. Радиоприемное устройство обнаружения сигнала чаще всего бывает двух-альтернативным (бинарное обнаружение). Здесь выносится решение D= = 1 (ДА), если в наблюдаемом поле или процессе сигнал есть. В противном случае выносится решение ' D — О (НЕТ).

Радиоприемное устройство различения (многоальтернативного) выносит решение D — I, I -■ 1, п, если в наблюдаемом поле или процессе присутствует /-й вариант сигнала и_с1 (г), передаваемый через канал связи. При п — 2 имеется бинарное различение,

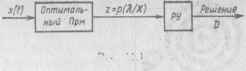
Рис. 11.1

широко распространенное в РПУ дискретных сигналов.

Радиоприемное устройство оценки параметра к сигнала выносит (в конце интервала наблюдения / == Т) решение D = к, причем параметр к считается на этом интервале наблюдения неизменным. Это радиоприемные устройства измерения параметров сигнала: частоты, фазы, амплитуды, групповой задержки, направления прихода волны.

Радиоприемное устройство оценки (фильтрации) непрерывного сообщения k(t), существенно изменяющегося на интервале наблюдения, выносит

текущую оценку D (t) — k(t), t£ Т. Это следящие радиоприемные устройства. Если к (г) — модулирующее напряжение сигнала, то процесс фильтрации сообщения эквивалентен процессу демодуляции. В ряде случаев фильтруется не параметр сигнала, а сам сигнал и_с (г, к).

Радиоприемное устройство разрешения сигналов работает в условиях, когда в наблюдаемом поле или процессе одновременно присутствует совокупность сигналов u_cl (t), I = \,п. От РПУ требуется либо обнаружить раздельно каждый из сигналов (разрешение — обнаружение), либо различить их всех (разрешение — различение), либо измерить или отфильтровать параметр каждого из сигналов (разрешение — оценка).

Байесово решение при произвольных сигналах и помехах. В условиях полной априорной определенности наилучшим считается [301 радиоприемное устройство, которое для любых решаемых задач распадается на оптимальный приемник (Прм) и решающее устройство (РУ) (рис. 11.1). Первый из них, на основе обработки процессов (11.1) с дискретной выборкой X =

. X (к), в которой закодирован параметр сигнала к, в момент времени t = Т формирует так называемую апостериорную плотность вероятностей, описываемую формулой Байеса [81:

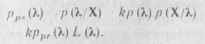
Здесь k р~^л (X) коэффициент, не зависящий от к; р_г, (к) р (к)--априорная плотность вероятностей; L (к) -= р (XX) функция правдоподобия.

При непрерывной обработке (Л/->--v 0) все плотности вероятностей в (11.2) переходят в функционалы плотностей вероятностей [81 вида р\(х (/)[ = = lim р (X), а функция правдопо-

Д*-0

добия — в функционал правдоподобия f (к) - lim L (к) - р [х иу'к\.

ДГ-0

В качестве критерия оптимальности при байесовом решении берется критерий минимума среднего риска [30], который и определяет структуру решающего устройства.

Структурные схемы оптимальных радиоприемных устройств при произвольных сигналах и помехах. Существует целый ряд оптимальных РПУ, использующих байесовы алгоритмы. Рассмотрим наиболее важные вари-

анты таких радиоприемных устройств.

1. О и т и м а л ь н ы е РПУ оценки параметра сигнал а. Если к ~ [k_lt ...

kj, км\ — векторный параметр, подлежащий оценке, то выходной эффект оптимального Прм г - р (к!\) на рис. 11.1 представляет собой многомерную функцию аргумента к. Тогда в качестве решения принимается оптимальная оценка D = -к (X) в виде одной из характерных точек (мода, медиана, центр тяжести) этой многомерной апостериорной плотности вероятностей.

Качество байесовых оценок в оптимальном РПУ (рис. 11.1) и, в частности, их потенциальная точность существенно зависят от функции правдоподобия L (к), входящей в виде сомножителя в апостериорную плотность вероятностей (11.2). Эта функция существенно зависит от соотношения сигнал'шум q Э_с/Э_ш на входе РПУ (рис. 11.2, а). При q < 1 видны многочисленные шумовые (ложные) выбросы, не соответствующие истинной

оценке к. При q 4, в частности, имеется двузначность отсчета с ложной оценкой к'. Лишь при с/ > 10 остается единственный правильный пик истинной оценки.

При формировании в оптимальном РПУ (рис. 11.1) выходного эффекта г (л) = р (к/Х) =* kp (к) L (к) возможны два частных случая:

а) априорная и апостериорная точности оценок сравнимы (рис. 11.2, б). Априорная плотность вероятностей р (к), может существенно сгладить шумовые выбросы функции правдоподобия и благоприятно повлиять на неоднозначность отсчета;

б) апостериорная точность значительно выше априорной (рис. 11.2,в). Апостериорная плотность вероятностей практически совпадает с функцией правдоподобия и выходной эффект оптимального Прм

г(к) р(Щ) wL(k) = p(%lk). (11.3)

Если при этом в РУ (рис. 11.2) в качестве оптимальной оценки берется точка максимума функции правдоподобия (11.3), то оценка к=[ку, ...

.... kj..... к_м\ называется максимально правдоподобной и часто используется в теории оптимального приема 1301.

2. Оптимальные РПУ м.ногоальтернати в н о г о различения. Здесь параметр к дискретен и соответствует набору к_ь i = 1, М исходных ситуаций присутствия в смеси (11.1) t-й копии сигнала u_ci (t) - и_с (t, к = k_t). Дискретно также решение D =-- Dj, j = 1, М, когда принимается гипотеза о присутствии в смеси (11.1) /-й копии сигнала.