Сигнал как аналитическая функция
Федеральное агентство связи
ГОУ ВПО «Сибирский государственный университет
телекоммуникаций и информатики»
Уральский технический институт связи и информатики (филиал)
АНАЛИЗ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ
В СИСТЕМЕ MATLAB
Методические указания к выполнению домашних заданий
по дисциплине «Радиотехнические цепи и сигналы»
для студентов всех форм обучения
специальностей 200700 – Радиотехника,
Екатеринбург
УДК 621.381
Составитель М. П. Трухин
Научный редактор доц., канд.техн.наук В. Г. Коберниченко
Анализ радиотехнических сигналов в системе MATLAB: методические указания к выполнению домашних заданий / М. П. Трухин – Екатеринбург: УрТИСИ, 2006. 48 с
Приведены задания и методические указания по их выполнению с использованием математической системы MATLAB.
Библиогр.: 9 назв. Табл.2. Рис.37.
Подготовлено кафедрой ОПД
ОГЛАВЛЕНИЕ
1 ПРЕДСТАВЛЕНИЕ СИГНАЛОВ В СИСТЕМЕ MATLAB.................................................... 4
1.1 Сигнал как аналитическая функция.................................................................................... 4
1.2 Сигнал как конечный взвешенный набор известных функций................................... 5
2 ДОМАШНЕЕ ЗАДАНИЕ 1...................................................................................................... 11
2.1 Содержание задания........................................................................................................... 11
2.2 Варианты исследуемых сигналов................................................................................... 12
2.3 Пример выполнения задания 1....................................................................................... 16
2.3.1 Математическая модель сигнала на одном периоде повторения......................... 16
2.3.2 Математическая модель периодического сигнала.................................................... 17
2.3.4 Распределение энергии в спектре периодического сигнала................................. 19
2.3.5 Спектральная плотность непериодического сигнала............................................... 21
2.3.6 Энергетический спектр непериодического сигнала.................................................. 22
2.3.7 Автокорреляционная функция непериодического сигнала.................................... 23
2.3.8 Функция взаимной корреляции непериодического сигнала и меандра с амплитудой, равной максимальному значению сигнала........................................................................... 24
3 ДОМАШНЕЕ ЗАДАНИЕ № 2.................................................................................................. 27
3.1 Содержание задания........................................................................................................... 27
3.2 Пример выполнения задания № 2................................................................................... 28
3.2.1 Математическая модель амплитудно-модулированного сигнала......................... 28
3.2.2 Дискретный спектр АМК с периодическим модулирующим сигналом................. 29
3.2.3 Амплитудно-модулированное колебание с одной боковой полосой................... 30
3.2.4 Фазо-модулированный сигнал....................................................................................... 31
3.2.5 Частотно-модулированный сигнал............................................................................... 33
3.2.6 Определение интервала дискретизации.................................................................... 35
4 ДОМАШНЕЕ ЗАДАНИЕ 3...................................................................................................... 36
4.1 Содержание задания........................................................................................................... 36
4.2 Пример выполнения задания 3........................................................................................ 36
4.2.1 Дискретная модель сигнала s(t)...................................................................................... 36
4.2.2 Дискретная модель смещённого сигнала sсм(t)........................................................... 39
4.2.3 Дискретная модель зашумлённого сигнала sШ(t)........................................................ 40
4.2.4 Представление сигналов в базисе Чёбышева........................................................... 41
4.2.5 Представление сигналов в мультипликативном однородном базисе................. 43
4.2.6 Представление сигналов в базисе Уолша................................................................... 45
БИБЛИОГРАФИЧЕСИЙ СПИСОК........................................................................................... 48
1 ПРЕДСТАВЛЕНИЕ СИГНАЛОВ В СИСТЕМЕ MATLAB
Сигнал как аналитическая функция
Сигнал представляется в виде математического соотношения, в котором устанавливается связь между переменной, которой сопоставлено свойство сигнал, и конечным набором других переменных (свойств), которые называются параметры сигнала. Например, в непрерывном гармоническом колебании 
параметрами сигнала могут быть амплитуда 
, циклическая частота 
и начальная фаза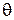 
.
При моделировании такого сигнала в системе MATLAB как некоторого объекта, устанавливающего непрерывную связь между параметрами сигнала и его значением, можно использовать следующие варианты:
1. Представление сигнала в виде команды в командной строке. Сначала в рабочее пространство вносятся фиксированные значения параметров:
Uo = 1;
f = 10;
theta = 0;
задаётся набор точек, в которых (или которой) сигнал должен быть вычислен:
t = 0:0.01:1;
а потом по команде
xt = Uo*sin(2*pi*f*t+theta);
в рабочем пространстве появляется соответствующий набор значений сигнала.
2. Представление аналитического выражения сигнала в виде строки. Если заданы параметры сигнала, т.е. все переменные в его аналитическом выражении, то это выражение можно записать сначала в форме строки
s = 'Uo*sin(2*pi*f*t+theta)';
а затем вычислять одно или несколько его значений с помощью М-функции eval:
xs = eval(s);
3. Представление сигнала в виде встроенной строки. Такое представление – нечто среднее между представлением сигнала просто строкой и М-функцией, поскольку в этом случае при вычислении сигнала его параметры можно задавать как входные переменные. Сначала записывается встроенная строка (inline-объект)
y = inline('sin(2*pi*f*t + theta)','t', 'f', 'theta')
результат выполнения которой отображается в виде формы обращения к функции:
Inline function: y(t,f,theta) = sin(2*pi*f*t + theta)
Значения сигнала определяются при выполнении команды обращения, например,
xg = y(t, f, 0)
4. Представление сигнала в виде М-функции. Это наиболее универсальный и часто используемый вид задания сигналов. Поскольку в системе MATLAB можно использовать переменное количество входных (nargin) и выходных (nargout) параметров, то некоторые из них могут при вызове М-функции опускаться.
function y = sinf(t,f,theta)
% y = sinf(t,f,theta)
% y = sinf(2*pi*f*t + theta)
if nargin = = 3
y = sinf(2*pi*f*t + theta);
elseif nargin = = 2
y = sinf(2*pi*f*t);
end
Вычисление значений сигнала для заданного набора параметров выполняется по команде
xf = sinf(t, f, theta);
или, например, по команде
xf = sinf(t, 10);
5. Представление сигнала в символическом виде. Такое представление обладает наибольшей универсальностью, так как позволяет не только вычислять значения сигнала в любой момент времени, но и определять символические (по-существу, аналитические) результаты его математических преобразований: производной, интеграла, разложения в ряды, интегральных преобразований.
Сначала задаётся описание параметров как символических переменных:
syms t f theta Uo
затем аналитическое выражение сигнала представляется строкой:
s = 'Uo*sin(2*pi*f*t+theta)';
Результат дифференцирования гармонического сигнала по времени
ds = diff(s,'t')
выглядит так (ds – тоже символьное представление):
ds = 2*Uo*cos(2*pi*f*t+theta)*pi*f ,
что соответствует аналитическому выражению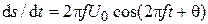 
. Переход к численным значениям выполняется с использованием функции eval при условии задания параметров в рабочем пространстве:
Uo = 1; theta = 0; t = 0:0.01:1;
xf = eval(s)
Так как частота f в этом примере численно не определена, то результат обращения к функции eval представляет строку из 101 символьного выражения:
xf =[0, sin(1/10*pi*f), sin(1/5*pi*f), ..., sin(20*pi*f)]