Сызықтық операторларға амалдар қолдану
n  1. Сызықтық операторлар жиыны.
1. Сызықтық операторлар жиыны.
Сызықтық операторлардың теңдігі
F өрісінде берілген n өлшемді V  векторлық кеңістігіне әсер ететін сызықтық операторлардың жиынын L(V
векторлық кеңістігіне әсер ететін сызықтық операторлардың жиынын L(V  ) деп белгілейік. Сонда
) деп белгілейік. Сонда
L(V  ) =
) = 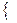
 |
|  : V
: V 
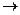 V
V  &
&  – сызықтық
– сызықтық 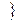 .
.
Сызықтық операторлардың теңдігі, әдеттегіше, бейнелеулердің теңдігі ретінде анықталады:  ,
, 
 L(V
L(V  )
)
def
(  =
=  )
) 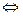 (
(  х
х  V
V 
 (х) =
(х) =  (х) ) (*)
(х) ) (*)
Егер екі сызықтық оператор тең болса, онда белгілі – бір базистегі олардың матрицалары да тең болады: 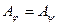 .
.
n  2. Сызықтық операторларды қосу
2. Сызықтық операторларды қосу
Айталық,  ,
, 
 L(V
L(V  ) болсын. Мынадай заңдылық анықтайық:
) болсын. Мынадай заңдылық анықтайық:
(  +
+  ) (х) =
) (х) =  (х) +
(х) +  (х) , х
(х) , х  V
V  (4)
(4)
Осы анықталған  +
+  заңдылығы
заңдылығы  мен
мен  сызықтық операторларының қосындысы деп аталады.
сызықтық операторларының қосындысы деп аталады.
Лемма.  +
+  қосындысы сызықтық оператор болады.
қосындысы сызықтық оператор болады.
Дәлелдеу.  х
х  V
V  үшін
үшін  (х) және
(х) және  (х) векторлары бірмәнді анықталған, себебі
(х) векторлары бірмәнді анықталған, себебі  ,
,  – сызықтық операторлар. Векторлық кеңістікте + БАО болғандықтан,
– сызықтық операторлар. Векторлық кеңістікте + БАО болғандықтан,  (х) +
(х) +  (х) векторы да бірмәнді анықталады. Онда
(х) векторы да бірмәнді анықталады. Онда  +
+  заңдылығы бейнелеу (оператор) болады. Сызықтық болатынын көрсетейік.
заңдылығы бейнелеу (оператор) болады. Сызықтық болатынын көрсетейік.
(4)  ,
,  с.оп.
с.оп.
(  +
+  )(
)(  х+
х+  у) =
у) =  (
(  х+
х+  у) +
у) +  (
(  х +
х +  у) =
у) = 
 (х)+
(х)+ 
 (у)+
(у)+ 
 (х)+
(х)+ 
 (у)= =|в.к.акс. | =
(у)= =|в.к.акс. | =  (
(  (х)+
(х)+  (х)) +
(х)) +  (
(  (у)+
(у)+  (у)) = |(4) бой. |=
(у)) = |(4) бой. |=  (
(  +
+  )(х)+
)(х)+  (
(  +
+  )(у).
)(у).
Онда  +
+ 
 L(V
L(V  ).
).
Анықтама. Берілген  және
және  сызықтық операторларына
сызықтық операторларына  +
+  сызықтық операторын сәйкестікке қоятын амалды сызықтық операторларды қосу амалы деп атайды.
сызықтық операторын сәйкестікке қоятын амалды сызықтық операторларды қосу амалы деп атайды.
Сонымен, L(V  ) жиынында + БАО-сы анықталды.
) жиынында + БАО-сы анықталды.
Қосынды  +
+  сызықтық оператордың матрицасын анықтайық. V
сызықтық оператордың матрицасын анықтайық. V  кеңістігі- нің қандай да бір е
кеңістігі- нің қандай да бір е  , е
, е  , ... , е
, ... , е  базисіндегі
базисіндегі  сызықтық операторының матрицасы А
сызықтық операторының матрицасы А  ,
,  сызықтық операторының матрицасы А
сызықтық операторының матрицасы А 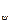 болсын. Қосынды
болсын. Қосынды
 +
+  сызықтық операторының осы базистегі матрицасын А
сызықтық операторының осы базистегі матрицасын А 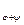 деп белгілейік
деп белгілейік
Онда (2¢) бойынша 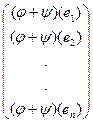 = А
= А 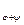
 ; екінші жағынан, (4) бойынша
; екінші жағынан, (4) бойынша
||
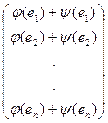 =
= 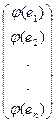 +
+ 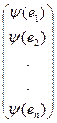 = А
= А 
 + А
+ А 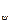
 = =|матрицаларды көбейту қосуға қатысты дистрибутивті болғандықтан| =
= =|матрицаларды көбейту қосуға қатысты дистрибутивті болғандықтан| =
=( А  + А
+ А 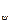 )
)  ; бұдан, вектордың базис арқылы жіктелуінің бірмәнділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады: А
; бұдан, вектордың базис арқылы жіктелуінің бірмәнділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады: А 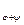 = А
= А  + А
+ А 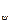 . (*)
. (*)
(Соңғы теңдікті өзіңіз сөзбен оқыңыз).
L(V  ) жиынында анықталған + БАО-ның төмендегідей қасиеттері бар:
) жиынында анықталған + БАО-ның төмендегідей қасиеттері бар:
1  .
. 
 ,
, 
 L(V
L(V  )
)  +
+  =
=  +
+ 
2  .
. 
 ,
,  ,
, 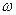
 L(V
L(V  ) (
) (  +
+  )+
)+ 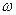 =
=  +(
+(  +
+ 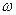 )
)
3  .
. 

 L(V
L(V  )
)  +
+ 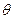 =
= 
4  .
. 

 L(V
L(V  )
) 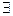 (–
(–  )
)  L(V
L(V  )
)  +(–
+(–  ) =
) = 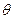 .
.
Бұл қасиеттерді өздеріңіз дәлелдеңіз. Нұсқау. 4  қасиетте алдымен (–
қасиетте алдымен (–  ) заңдылығын анықтап алу керек, сонан кейін оның сызықтық екенін көрсету керек, соңында
) заңдылығын анықтап алу керек, сонан кейін оның сызықтық екенін көрсету керек, соңында  -ге қарама-қарсы болатынын дәлелдеу керек.
-ге қарама-қарсы болатынын дәлелдеу керек.
Анықталған (4) амалдың қасиеттерінен L(V  ) жиыны абельдік группа болатыны шығады:
) жиыны абельдік группа болатыны шығады: 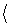 L(V
L(V  ), +
), + 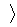 – абельдік группа.
– абельдік группа.
n  3. Сызықтық операторды скалярға көбейту
3. Сызықтық операторды скалярға көбейту
Айталық, 
 L(V
L(V  ),
), 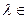 F болсын. Мынадай заңдылық анықтайық:
F болсын. Мынадай заңдылық анықтайық:
( 
 )(х) =
)(х) = 
 (х) , х
(х) , х  V
V  (5)
(5)
Осы анықталған 
 заңдылығы
заңдылығы  сызықтық операторының
сызықтық операторының  скалярына көбейтіндісі деп аталады.
скалярына көбейтіндісі деп аталады.
Лемма. (5) формуламен анықталған 
 заңдылығы сызықтық оператор болады.
заңдылығы сызықтық оператор болады.
Дәлелдеу.  сызықтық оператор болғандықтан
сызықтық оператор болғандықтан  х
х  V
V  үшін
үшін  (х) векторы бірмәнді анықталған. Векторлық кеңістіктегі скалярға көбейту амалының берілуінен
(х) векторы бірмәнді анықталған. Векторлық кеңістіктегі скалярға көбейту амалының берілуінен 
 (х) векторы да бірмәнді анықталатыны шығады. Онда
(х) векторы да бірмәнді анықталатыны шығады. Онда 
 заңдылығы бейнелеу (оператор) болады. Сызықтық болатынын көрсетейік.
заңдылығы бейнелеу (оператор) болады. Сызықтық болатынын көрсетейік.
(5)  с.о. в.к.акс.
с.о. в.к.акс.
( 
 )(
)(  х+
х+  у) =
у) = 
 (
(  х+
х+  у) =
у) =  (
( 
 (х) +
(х) + 
 (у) ) =
(у) ) = 

 (х) +
(х) + 

 (у) = = |в.к.акс.| =
(у) = = |в.к.акс.| =  (
( 
 (х)) +
(х)) +  (
( 
 (у)) = |(5) бой.| =
(у)) = |(5) бой.| =  (
( 
 )(х) +
)(х) +  (
( 
 )(у).
)(у).
Онда 

 L(V
L(V  ).
).
Анықтама. Берілген  сызықтық операторына
сызықтық операторына 
 сызықтық операторын сәйкестікке қоятын амалды сызықтық операторды скалярға көбейту амалы деп атайды.
сызықтық операторын сәйкестікке қоятын амалды сызықтық операторды скалярға көбейту амалы деп атайды.
Ескерту. Анықталған скалярға көбейту амалы L(V  ) жиынында сыртқы амал болады.
) жиынында сыртқы амал болады.
Осы 
 сызықтық операторының матрицасын анықтайық. V
сызықтық операторының матрицасын анықтайық. V  кеңістігінің қандай да бір е
кеңістігінің қандай да бір е  , е
, е  , ... , е
, ... , е  базисіндегі
базисіндегі  сызықтық операторының матрицасы А
сызықтық операторының матрицасы А  болсын. Анықталған
болсын. Анықталған 
 сызықтық операторының осы базистегі матрицасын А
сызықтық операторының осы базистегі матрицасын А 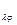 деп белгілейік.
деп белгілейік.
Онда (2¢) бойынша 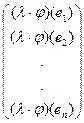 = А
= А 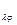
 ; екінші жағынан, (5) бойынша
; екінші жағынан, (5) бойынша
||
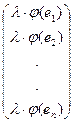 =
= 
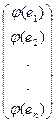 =
=  А
А 
 ; бұдан, вектордың базис арқылы жіктелуінің бірмәнділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады: А
; бұдан, вектордың базис арқылы жіктелуінің бірмәнділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады: А 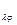 =
=  А
А  . (Теңдікті сөзбен оқыңыз).
. (Теңдікті сөзбен оқыңыз).
L(V  ) жиынында анықталған скалярға көбейту – сыртқы амалының мынадай қасиеттері бар:
) жиынында анықталған скалярға көбейту – сыртқы амалының мынадай қасиеттері бар:
1  .
. 

 L(V
L(V  )
) 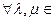 F (
F ( 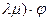 =
= 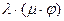
2  .
. 

 L(V
L(V  )
) 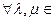 F (
F ( 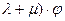 =
= 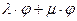
3  .
. 
 ,
, 
 L(V
L(V  )
) 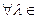 F
F  (
(  +
+  ) =
) = 
 +
+ 

4  .
. 

 L(V
L(V  ) 1·
) 1·  =
=  , мұндағы 1 – F өрісінің бірі.
, мұндағы 1 – F өрісінің бірі.
(Қасиеттердің дәлелдеуі өзбетімен).
(4), (5) амалдардың анықтамасы мен олардың қасиеттерінен L(V  ) жиынының өзі F өрісінде берілген векторлық кеңістік құрайтыны шығады:
) жиынының өзі F өрісінде берілген векторлық кеңістік құрайтыны шығады:
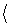 L(V
L(V  ), +,
), +, 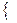

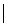
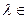 F
F 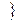
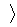 – векторлық кеңістік.
– векторлық кеңістік.
Сонда, өрісте берілген векторлық кеңістіктегі сызықтық операторлар жиыны, өзі, сол өрісте берілген векторлық кеңістік құрайды.
n  4. Сызықтық операторларды көбейту
4. Сызықтық операторларды көбейту
Айталық,  ,
, 
 L(V
L(V  ) болсын. Мынадай заңдылық анықтайық:
) болсын. Мынадай заңдылық анықтайық:
( 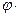
 ) (х) =
) (х) =  (
(  (х)) , х
(х)) , х  V
V  (6)
(6)
Осы анықталған 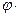
 заңдылығы
заңдылығы  мен
мен  сызықтық операторларының көбейтіндісі деп аталады.
сызықтық операторларының көбейтіндісі деп аталады.
Лемма. 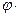
 көбейтіндісі сызықтық оператор болады.
көбейтіндісі сызықтық оператор болады.
Дәлелдеу.  сызықтық оператор болғандықтан,
сызықтық оператор болғандықтан,  х
х  V
V  үшін
үшін  (х) векторы бірмәнді анықталған, ал
(х) векторы бірмәнді анықталған, ал  де сызықтық оператор болғандықтан
де сызықтық оператор болғандықтан  (
(  (х)) векторы бірмәнді анықталған. Онда
(х)) векторы бірмәнді анықталған. Онда 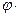
 заңдылығы бейнелеу (оператор) болады. Оның сызықтық болатынын тексерейік.
заңдылығы бейнелеу (оператор) болады. Оның сызықтық болатынын тексерейік.
(6)  с.оп.
с.оп.  с.оп. (6)
с.оп. (6)
( 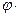
 )(
)(  х+
х+  у)=
у)=  (
(  (
(  х+
х+  у)) =
у)) =  (
( 
 (х)+
(х)+ 
 (у)) =
(у)) = 
 (
(  (х))+
(х))+ 
 (
(  (у)) =
(у)) =
=  (
( 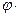
 )(х) +
)(х) +  (
( 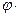
 )(у).
)(у).
Онда 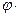

 L(V
L(V  ).
).
Анықтама. Берілген  және
және  сызықтық операторларына
сызықтық операторларына 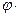
 сызықтық операторын сәйкестікке қоятын амалды сызықтық операторларды көбейту амалы деп атайды.
сызықтық операторын сәйкестікке қоятын амалды сызықтық операторларды көбейту амалы деп атайды.
Сонымен, L(V  ) жиынында · БАО-сы анықталды.
) жиынында · БАО-сы анықталды.
Көбейтінді 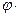
 сызықтық оператордың матрицасын анықтайық. V
сызықтық оператордың матрицасын анықтайық. V  кеңіс- тігінің қандай да бір е
кеңіс- тігінің қандай да бір е  , е
, е  , ... , е
, ... , е  базисіндегі
базисіндегі  сызықтық операторының матрицасы А
сызықтық операторының матрицасы А  ,
,  сызықтық операторының матрицасы А
сызықтық операторының матрицасы А 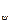 болсын. Көбейтінді
болсын. Көбейтінді 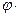
 сызықтық операторының осы базистегі матрицасын А
сызықтық операторының осы базистегі матрицасын А 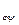 деп белгілейік.
деп белгілейік.
Онда (2¢) бойынша 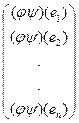 = А
= А 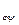 ·
·  ; екінші жағынан, (6) бойынша
; екінші жағынан, (6) бойынша
||
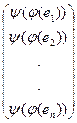 =
=  (
( 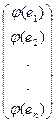 ) =
) =  (А
(А 
 ) = |
) = |  с.оп.|= А
с.оп.|= А 
 (
(  ) =
) =
= А 
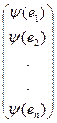 = А
= А  А
А 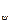
 ; бұдан, вектордың базис арқылы жіктелуінің бірмән- ділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады:
; бұдан, вектордың базис арқылы жіктелуінің бірмән- ділігінен, екі жіктелудің коэффициенттерінің теңдігі шығады:
А 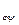 = А
= А  ·А
·А 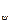 . (**)
. (**)
Соңғы теңдікті сөзбен оқыңыз.
L(V  ) жиынында анықталған · БАО-ның төмендегідей қасиеттері бар:
) жиынында анықталған · БАО-ның төмендегідей қасиеттері бар:
1  .
. 
 ,
,  ,
, 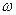
 L(V
L(V  ) (
) ( 
 )
) 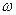 =
=  (
( 
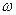 )
)
2  .
. 
 ,
,  ,
, 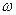
 L(V
L(V  ) (
) (  +
+  )
) 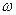 =
= 
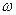 +
+ 
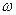
 &
& 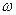 (
(  +
+  ) =
) = 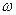
 +
+ 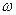

3  .
. 

 L(V
L(V  )
) 
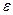 =
= 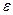
 =
= 
Бұл қасиеттерді өздеріңіз дәлелдеңіз.
Анықталған (4), (6) амалдар мен олардың қасиеттерінен L(V  ) жиыны бірі бар сақина болатыны шығады:
) жиыны бірі бар сақина болатыны шығады: 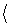 L(V
L(V  ), +, ·
), +, · 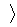 – бірі бар сақина.
– бірі бар сақина.
Сонда, өрісте берілген векторлық кеңістіктегі сызықтық операторлар жиыны сақина құрайды.Оны сызықтық операторлар сақинасы дейді.
Жоғарыда, §5-те біз, n өлшемді векторлық кеңістіктегі сызықтық операторлар мен n–ші ретті квадрат матрицалар арасында өзара бірмағыналы сәйкестік (биекция) болатынын көрдік. Ал осы §8-гі n  2, n
2, n  4 – дің нәтижесінен бұл сәйкестіктің аддитивті және мультипликативті болатыны шықты ( (*), (**) формулаларын қара). Онда, сызықтық операторлар сақинасы мен квадрат матрицалар сақинасы изоморфты болғаны:
4 – дің нәтижесінен бұл сәйкестіктің аддитивті және мультипликативті болатыны шықты ( (*), (**) формулаларын қара). Онда, сызықтық операторлар сақинасы мен квадрат матрицалар сақинасы изоморфты болғаны:
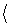 L(V
L(V  ), +, ·
), +, · 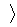
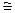
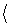 М
М  (F), +, ·
(F), +, · 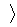 .
.
