Теоретическое введение

Электромагнитная индукция – это явление возникновения электродвижущей силы в контуре при изменении магнитного потока, пронизывающего контур. Если контур проводящий, то в нем возникает электрический индукционный ток. По закону Фарадея электродвижущая сила равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность контура:

. (1)

Магнитный поток, по определению, сквозь поверхность некоторого контура для однородного магнитного поля равен скалярному произведению вектора индукции магнитного поля В на вектор площади контура: Ф = ВS cos a. Угол a – это угол между вектором магнитной индукции и вектором площади. Вектор площади численно равен площади поверхности контура и направлен по нормали к контуру. Магнитный поток через поверхность контура имеет геометрический смысл: он пропорционален числу силовых линий, пронизывающих эту поверхность. Поток может быть изменен тремя способами: либо изменением индукции магнитного поля, либо изменением площади контура, либо изменением угла a, то есть поворотом контура в магнитном поле или, наоборот, магнитного поля относительно контура.

Если в магнитном поле находится катушка с некоторым числом витков, то витки можно представить как последовательно соединенные контуры. Тогда ЭДС электромагнитной индукции определится как сумма ЭДС всех витков, то есть как скорость изменения во времени суммы магнитных потоков через все витки. Эту сумму называют потокосцеплением (Y = S Ф_i). Для катушки ЭДС электромагнитной индукции равна скорости изменения потокосцепления:

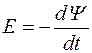. (2)

Направление индукционного тока определяется правилом Ленца: индукционный ток имеет такое направление, чтобы своим магнитным полем компенсировать то изменение магнитного потока, которое вызвало данный ток, или, индукционный ток имеет такое направление, чтобы препятствовать изменению причины, вызвавшей этот ток.

Явление взаимной индукции – это частный случай явления электромагнитной индукции, при котором изменение магнитного потока через контур обусловлено изменением силы электрического тока в другом контуре. Пусть два контура магнитно связаны друг с другом, то есть силовые линии магнитного поля, созданного одним контуром, пронизывают поверхность другого контура (рис. 1). Магнитный поток через поверхность второго контура будет пропорционален силе тока J в первом контуре. Пропорционально силе тока и потокосцепление катушки:

Ф=MJ,для катушек Y = MJ. (3)

Коэффициент пропорциональности M называется взаимной индуктивностью. Для неферромагнитных сред он постоянен, для ферромагнитных сред зависит от силы тока.

Подставив формулы (3) в уравнение закона Фарадея (1, 2), получим, что ЭДС взаимной индукции пропорциональна скорости изменения силы тока в проводниках, создающих магнитное поле:

. (4)

Направление индукционного тока во втором контуре определяется правилом Ленца. Например, при возрастании силы тока в первом контуре индукционный ток во втором контуре будет направлен противоположно, противодействуя возрастанию магнитного потока (рис. 1). При этом контуры отталкиваются под действием сил Ампера. При выключении – наоборот.

Рассчитать теоретически взаимную индуктивность можно лишь в некоторых случаях, например, для двух длинных катушек с общим сердечником (рис. 2). Магнитный поток в сердечнике, создаваемый током первой катушки равен Ф = BS = (mm₀n₁ J₁) S, где m₀ = 4p ∙10^-7 Гн/м – магнитная постоянная, m – магнитная проницаемость материала сердечника, – концентрация витков первой катушки, т. е. число витков на единицу длины l сердечника; S – площадь сечения сердечника.

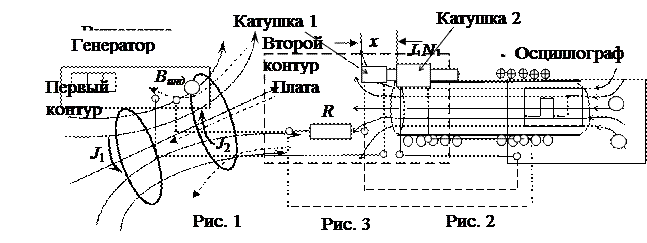
Сердечник катушек общий, поэтому тот же поток пронизывает витки второй катушки. Потокосцепление, связанное со всеми витками второй катушки равноY =ФN₂. Подставив формулу потока, число витков N₂ = n₂l и объем сердечника V = l S в формулу (3), получим для взаимной индуктивности двух катушек: M=mm₀n₁n₂V . Как видно она зависит от расположения контуров, их размеров, от магнитной проницаемости среды, от числа витков.

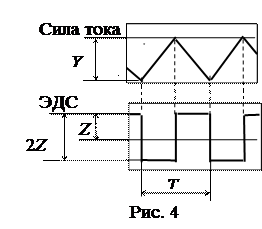
Экспериментальное измерение взаимной индуктивности двух катушек можно произвести, используя формулу (4), по величине ЭДС взаимной индукции. Первичная катушка подключена к генератору пилообразного напряжения (рис. 3). Поэтому сила электрического тока в катушке 1 изменяется по линейному закону: при возрастании напряжения J=с t, а при спаде J = J₀ – c t , как показано на осциллограмме (рис. 4). Во вторичной катушке возникает ЭДС взаимной индукции. Для измерения силы тока в первой катушке и ЭДС применяется осциллограф.

Скорость изменения силы тока определим как отношение амплитуды силы тока ко времени одного полупериода: . Период равен величине, обратной частоте генератора: 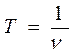. Тогда .

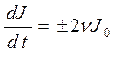Подставив скорость изменения силы тока в закон взаимной индукции (4), получим, что ЭДС во второй катушке будет постоянна , как во время возрастания силы тока в первой катушке, так и при спаде, но противоположной полярности (рис. 4). Отсюда взаимная индуктивность двух катушек может быть определена по формуле

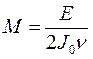. (5)

Если к осциллографу подключить вторичную катушку, то ЭДС взаимной индукции будет пропорциональна половине высоты прямоугольного импульса Z на экране осциллографа: Е=К_ЕZ , где К_Е – коэффициент усиления осциллографа в режиме измерения ЭДС.

Для измерения амплитуды силы тока в первичной катушке осциллограф подключают к выводам резистора R, по которому течет тот же ток, что и в катушке. По закону Ома сила тока в резисторе равна 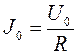. Амплитуду напряжения можно определить по высоте Y треугольного пика на экране осциллографа: U₀=K_JY. Тогда амплитуду силы тока можно рассчитать по формуле 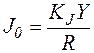. Здесь К_J – коэффициент усиления осциллографа в режиме измерения силы тока в первичной катушке. Таким образом, подставив формулы для ЭДС и силы тока в уравнение (5), получим для экспериментального измерения взаимной индуктивности формулу

. (6)