Иррациональные неравенства
Некоторые виды иррациональных неравенств.
О. 4.1. Неравенства, в которых переменная или выражение, содержащее переменную, входит под знаком радикала, называются иррациональными.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень. Если в неравенство входит квадратный корень, то в квадрат; если входит корень третьей степени − в куб и т. д. Однако, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. В противном случае можно получить неравенство неравносильное исходному неравенству. Простой пример: несмотря на то, что  − верное неравенство, при возведении его в квадрат, получим неравенство
− верное неравенство, при возведении его в квадрат, получим неравенство  ,которое уже верным не является.
,которое уже верным не является.
Для решения иррациональных неравенств, содержащих корни чётных степеней, приходится обязательно находить ОДЗ, поэтому наиболее универсальным является способ равносильных преобразований. Рассмотрим схемы решения наиболее часто встречающихся иррациональных неравенств.
1).Неравенства вида 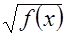 <
< 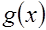 (6)
(6) 
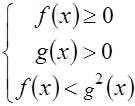 .
.
2).Неравенства вида 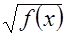
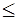
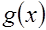 (7)
(7) 
 .
.
3).Неравенства вида 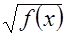 >
> 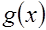 (8)
(8) 


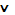
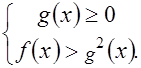
4).Неравенства вида 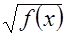
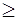
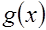 (9)
(9) 


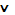
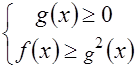 .
.
5).Неравенства вида 
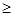 0 (или
0 (или  ) (10) решаются при помощи определения нестрогого неравенства.
) (10) решаются при помощи определения нестрогого неравенства.
Например, 
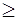 0
0 

6).Неравенства вида 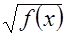
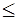
 (11)
(11) 

Пример 8. Решить неравенство 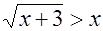 .
.
Δ По схеме 3) данное неравенство равносильно совокупности двух систем
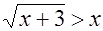


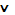
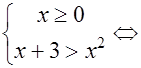

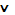




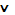


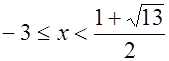 .
.
Ответ:  .
.
Пример 9. Решить неравенство 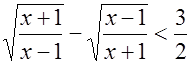 .
.
Δ Обозначим  , тогда
, тогда  , где
, где 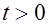 .
.
Исходное неравенство принимает вид:  .
.
Учитывая условие 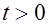 , получаем:
, получаем: 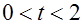 .
.
Воспользовавшись обратной подстановкой, решим неравенство: 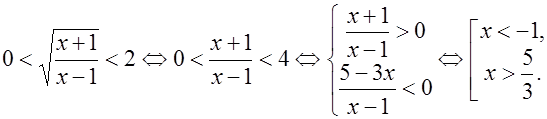
Ответ:  .
.
Учебная карта к занятию 6
Задания уровня А
1.1 Решите уравнения а) 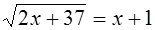 ,
,
б) 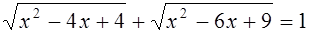 .
.
Задания уровня В
2.1 Решите уравнения а) 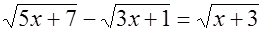 ,
,
б) 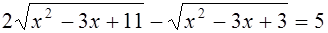 .
.
2.2 Решите неравенства а)  ,
,
б) 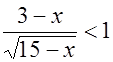 , в)
, в) 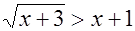 .
.
Задания уровня С
3.1Решите уравнение 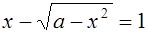 .
.
Домашнее задание
1.2 Найдите область определения функции
а) 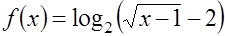 , б)
, б)  ,
,
в) 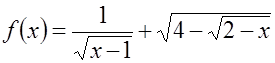 .
.
2.3 Найдите область определения функции
а) 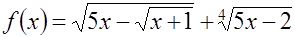 ;
;
б)  .
.
2.4 Решите неравенство 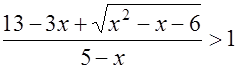 .
.
3.2Для каждого действительного значения параметра а найдите решение неравенства  .
.
Ответы и указания к заданиям
1.1а)  ; б)
; б) 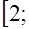
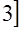
 Указание. Свернуть подкоренные выражения в квадрат, применить свойство модуля:
Указание. Свернуть подкоренные выражения в квадрат, применить свойство модуля: 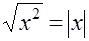 . 1.2а)
. 1.2а)  . Указание. По свойству логарифмической функции нахождение
. Указание. По свойству логарифмической функции нахождение 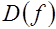 сводится к решению неравенства
сводится к решению неравенства 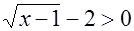 б)
б) 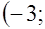
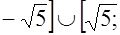
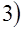 , в)
, в) 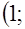
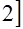 . Указание. По свойству корня чётной степени нахождение
. Указание. По свойству корня чётной степени нахождение 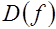 сводится к решению системы неравенств:
сводится к решению системы неравенств:  .
.
2.1а) 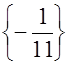 . Указание. См. пример 2; б)
. Указание. См. пример 2; б)  . Указание. Ввести замену:
. Указание. Ввести замену:  .
.
2.2а) 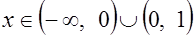 . Указание. Ввести замену:
. Указание. Ввести замену:  . б)
. б)  , в)
, в) 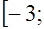
 . 2.3а)
. 2.3а) 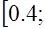
 ; б)
; б)  . Указание. См. пример 1.2.
. Указание. См. пример 1.2.
2.4 
 Указание. Привести неравенство к стандартному виду:
Указание. Привести неравенство к стандартному виду:  . Затем найти ОДЗ данного неравенства и перейти к равносильной совокупности систем (с учётом ОДЗ). 3.1
. Затем найти ОДЗ данного неравенства и перейти к равносильной совокупности систем (с учётом ОДЗ). 3.1 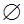 , если
, если 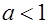 ;
;  , если
, если 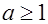 . Указание. Путём уединения радикала получить уравнение вида
. Указание. Путём уединения радикала получить уравнение вида  =
= 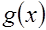 (3), которое равносильно системе (4), решаемой при помощи равносильных преобразований. 3.2
(3), которое равносильно системе (4), решаемой при помощи равносильных преобразований. 3.2 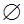 ,если
,если 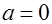 ;
; 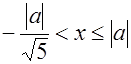 , если
, если  .
.
