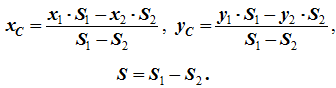Устойчивость при опрокидывании, коэффициент устойчивости

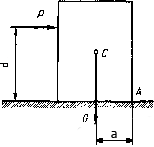
Составим сумму моментов задаваемых сил Р и G относительно опорной точки А:

Pd=Ga

Назовем абсолютные величины моментов сил G и Р относительно точки А удерживающим и опрокидывающим моментами:

M_уд=Ga

M_опр=Pd

Устойчивость при опрокидывании в технике принято определять отношением величины удерживающего момента к величине опрокидывающего момента:

K_у= M_уд/ M_опр

Это отношение называют коэффициентом устойчивости. Очевидно, что в случае предельной устойчивости коэффициент устойчивости равен единице, а в случае устойчивого состояния

K_у > 1.

Сила тяжести, центр тяжести, методы определения центра тяжести

Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести

Fт=GMm/R2

где М - масса Земли; R - радиус Земли.

Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле (2,28) модуль ускорения свободного падения g находят по формуле

g=Fт/m=GM/R2.

Из формулы следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы следует, что Fт = mg. В векторном виде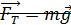

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела.

Способы определения координат центра тяжести.

1. Аналитический (путем интегрирования).

2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3. Экспериментальный (метод подвешивания тела).

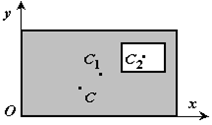
4. Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны

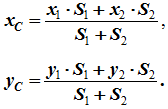
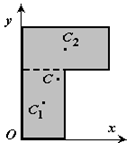
5. Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры :