Для самостоятельного решения. 1.1.01. Первую половину времени своего движения автомобиль двигался со скоростью v1=80 км/ч, а вторую половину времени – со скоростью v2=40 км/ч
1.1.01. Первую половину времени своего движения автомобиль двигался со скоростью v1=80 км/ч, а вторую половину времени – со скоростью v2=40 км/ч. Какова средняя скорость движения <v> движения автомобиля?
Ответ: а) <v>=50 км/ч; б) <v>=70 км/ч; в) <v>=6 км/ч; г) <v>=80 км/ч; д) <v>=60 км/ч.
1.1.02. Первую половину своего пути автомобиль двигался со скоростью v1=80 км/ч, а вторую половину пути – со скоростью v2=40 км/ч. Какова средняя скорость движения <v> движения автомобиля?
Ответ: а) <v>=53,3 км/ч; б) <v>=63,3 км/ч; в) <v>=73,3 км/ч;
г) <v>=43,3 км/ч; д) <v>=33,3 км/ч.
1.1.03. Уравнение движения материальной точки имеет вид x=2+t–0,5t2. Найти скорость v точки в момент времени t=2 с.
Ответ: а) v=-2 м/с; б) v=1 м/c; в) v=-1 м/с; г) v=2 м/с; д) v=
=-2,5 м/с.
1.1.04. Уравнение движения материальной точки вдоль оси X имеет вид x=2+t-0,5t2. Найти ускорение a точки.
Ответ: а) a=2 м/с2; б) a= -2 м/с2; в) a= -1 м/с2; г) a=1 м/с2;
д) a=1,2 м/с2.
1.1.05. Две материальные точки движутся согласно уравнениям x1=10+t+2t2 и x2=3+2t+0,2t2. В какой момент времени скорости этих точек одинаковы?
Ответ: а) t=2 с; б) t=3 с; в) t=0,28 с; г) t= -2,8 с; д) t=2,8 с.
1.1.06. Две материальные точки движутся согласно уравнениям: x1=4t+8t2-16t3 и x2=2t-4t2+t3. В какой момент времени ускорения этих точек будут одинаковы?
Ответ: а) t=0,54 с; б) t=0,44 с; в) t=0,34 с; г) t=0,24 с; д) t=0,14 с.
1.1.07. Две материальные точки движутся согласно уравнениям: x1=4t+8t2-16t3 и x2=2t-4t2+t3. Найти скорости этих точек в момент времени, когда их ускорения одинаковы.
Ответ: а) v1=36 м/с; v2=17 м/с; б) v1=3,6 м/с; v2=17 м/с;
в) v1=5,6 м/с; v2=-17 м/с; г) v1=17 м/с; v2=-39,6 м/с; д) v1=39,6 м/с; v2=-17 м/с.
1.  1.08. Точка движется по окружности радиусом R=4 м. Закон ее движения выражается уравнением s=8-2t2. Определить момент времени t, когда нормальное ускорение аn точки равно 9 м/с2.
1.08. Точка движется по окружности радиусом R=4 м. Закон ее движения выражается уравнением s=8-2t2. Определить момент времени t, когда нормальное ускорение аn точки равно 9 м/с2.
Ответ: а) t=1,5 с; б) t=2,5 с; в) t=1,5 с; г) t=3,5 с; д) среди приведенных ответов правильного нет.
1.1.09. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1.19). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти тангенциальное ускорение точки, лежащей на поверхности вала.
Ответ: а) at=4 м/с2; б) at=0,04 м/с2; в) at=0,4 м/с2; г) at=
=0,08 м/с2; д) at=0,8 м/с2.
1.1.10. На вал радиусом 10 см намотана нить, к концу которой привязана гиря (рис. 1.19). Опускаясь равноускоренно, гиря прошла расстояние 200 см за 10 с. Найти нормальное ускорение точки, лежащей на поверхности вала, в конечный момент движения.
Ответ: а) an=16 м/с2; б) an=0,16 м/с2; в) an=1,6 м/с2; г) an= =160 м/с2; д) an=0,016 м/с2.
1.1.11. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося диска, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30о с вектором ее линейной скорости (рис. 1.20).
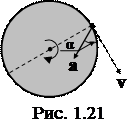 Ответ: а) an/at=0,5; б) an/at=0,8; в) an/at=0,68; г) an/at=0,7;
Ответ: а) an/at=0,5; б) an/at=0,8; в) an/at=0,68; г) an/at=0,7;
д) an/at=0,58.
1.1.12. Найти угловое ускорение колеса, если известно, что через 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α=60о с направлением линейной скорости этой точки (рис. 1.21).
Ответ: а) e=44 с-2; б) e=4,4 с-2; в) e=0,044 с-2; г) e=440 с-2;
д) e=0,43 с-2.
1.1.13. Стационарный искусственный спутник движется по окружности в плоскости земного экватора, оставаясь, все время над одним и тем же пунктом земной поверхности. Определить угловую скорость w спутника.
Ответ: а) w=7,27∙10-5 рад/с; б) w=3∙10-5 рад/с; в) w=7 рад/с;
г) w=5,3 рад/с; д) w=4,3×10-5 рад/с.
1.1.14. Определить нормальное ускорение точек, лежащих на земной поверхности на широте Москвы (j=58o, R3=6400 км).
Ответ: а) anМ=0,18 м/с2; б) anМ=1,8 м/с2; в) anМ=18 м/с2;
г) anМ=180 м/с2; д) anМ=0,018 м/с2.
1.1.15. Определить линейную скорость точек, лежащих на земной поверхности на экваторе (R3=6400 км).
Ответ: а) vэ=4,65 м/с; б) vэ=46,5 м/с; в) vэ=0,465 м/с; г) vэ= =465 м/с; д) vэ=4650 м/с.
1.1.16. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=А+2t+1t3. Найти угловую скорость w через время t=2,00 с после начала движения.
Ответ: а) w=0,14 рад/с; б) w=1,4 рад/с; в) w=24 рад/с; г) w=
=14 рад/с; д) w=2,4 рад/с.
1.1.17. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=А+2t+t3. Найти угловое ускорение e в момент времени t=0,5 c.
Ответ: а) e=3 рад/с2; б) e=1 рад/с2; в) e=2 рад/с2; г) e=
=0,3 рад/с2; д) e=0,03 рад/с2.
1.1.18. Диск радиусом 0,1 м вращается согласно уравнению j=10+20t - 2t2. Определить по величине тангенциальное ускорение точек на окружности диска.
Ответ: а) at=0,4 м/с2; б) at=-4 м/с2; в) at=-0,8 м/с2; г) at=0,8 м/с2; д) at=-0,4 м/с2.
1.1.19. Диск радиусом 0,1 м вращается согласно уравнению j=10+20t – 2t2. Определить по величине нормальное ускорение точек на окружности диска для момента времени t=4с.
Ответ: а) an=1,6 м/с2; б) an=2,6 м/с2; в) an=0,6 м/с2; г) an=16 м/с2; д) an=0,16 м/с2.
1.1.20. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м. Уравнение движения автомобиля j=10+10t–0,5t2. Найти полное ускорение автомобиля в момент времени t=9 с.
Ответ: а) а=7,05 м/с2; б) а=8,05 м/с2; в) а=10,5 м/с2; г) а= =70,5 м/с2; д) а=0,5 м/с2.
1.1.21. Диск радиусом 0,1 м вращается согласно уравнению j=10+20t-2t2. Определить по величине полное ускорение точек на окружности диска для момента времени t=4с.
Ответ: а) a=1 м/с2; б) a=0,65 м/с2; в) a=2,65 м/с2; г) a=1,65 м/с2; д) a=6,5 м/с2.
1.1.22. Материальная точка совершает гармоническое колебание, уравнение которого имеет вид: x=3coswt. Период колебаний T=2 c. Определить скорость материальной точки в момент времени 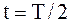 .
.
Ответ: а) v=0 м/с; б) v=1 м/с; в) v=2 м/с; г) v=2,5 м/с; д) v=3 м/с.
1.1.23. Материальная точка совершает гармоническое колебание, уравнение которого имеет вид: x=2sinwt. Период колебаний T=5 c. Определить скорость материальной точки в момент времени 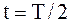 .
.
Ответ: а) v=1,5 м/с; б) v=-2,5 м/с; в) v=3,5 м/с; г) v=4,5 м/с;
д) v=5,5 м/с.
1.1.24. Материальная точка совершает гармоническое колебание, уравнение которого имеет вид: x=3coswt. Период колебаний T=2 c. Определить ускорение материальной точки в момент времени 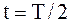 .
.
Ответ: а) a=9,6 м/с2; б) a=19,6 м/с2; в) a=29,6 м/с2; г) a=39,6 м/с2; д) a=49,6 м/с2.
1.1.25. Материальная точка совершает гармоническое колебание, уравнение которого имеет вид: x=2sinwt. Период колебаний T=5 c. Определить ускорение материальной точки в момент времени  .
.
Ответ: а) a=3 м/с2; б) a=2 м/с2; в) a=1 м/с2; г) a=0 м/с2;
д) a=0,5 м/с2.
1.1.26. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям: x=3cos[2p(t+0,5)]; y=4cos(2pt). Найти уравнение траектории движения точки.
Ответ: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 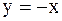 ;
;
д)  .
.
1.1.27. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям: x=3coswt; y=2sinwt. Найти уравнение траектории точки.
Ответ: а)  ; б)
; б)  ; в)
; в) 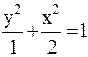 ;г)
;г) 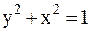 ; д)
; д) 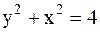 .
.
1.1.28. Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 0,05 м, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение равно 0,025 м.
Ответ: а) v=140 м/с; б) v=14 м/с; в) v=1,4 м/с; г) v=0,14 м/с;
д) v=0,014 м/с.
1.1.29. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний T=24 с, начальная фаза j0=0.
Ответ: а) t=1 с; б) t=1,5 с; в) t=2 с; г) t=2,5 с; д) t=3 с.
1.1.30. Начальная фаза гармонического колебания j0=0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
Ответ: а) t=T/4; б) t=T/5; в) t=T/3; г) t=T/2; д) t=T/6.
1.1.31. Тело массой m=0,5 кг движется прямолинейно, причем зависимость пройденного телом пути S от времени t дается уравнением: S=A-Bt+5t2-t3. Найти силу F, действующую на тело в конце первой секунды движения.
Ответ: а) F=0,2 Н; б) F=2 Н; в) F=3,5 Н; г) F=0,35 Н;
д) среди приведенных ответов правильного нет.
1.1.32. Материальная точка массой 2 кг движется под действием некоторой силы согласно уравнению x=2+5t+t2-0,2t3. Найти значение этой силы в момент времени t=2 с.
Ответ: а) Т=0,8 Н; б) Т=1,8 Н; в) Т=-0,8 Н; г) Т=-1,8 Н;
д) Т=2,8 Н.
1.1.33. Материальная точка движется под действием некоторой силы согласно уравнению Х=2+5t+t2-0,2t3. В какой момент времени значение этой силы равно нулю?
Ответ: а) t=5,67 с; б) t=1,67 с; в) t=2,67 с; г) t=4,67 с; д) t=3,67 с.
1.1.34. Под действием постоянной силы 10 Н тело движется прямолинейно так, что зависимость пройденного телом расстояния от времени задается уравнением: S=5-2t+t2. Найти массу тела.
Ответ: а) m=5 кг; б) m=7 кг; в) m=9 кг; г) m=11 кг; д) m=15 кг.
1.1.35. Сила F сообщает телу массой m1=2 кг ускорение a1=1 м/с2. Телу какой массы эта сила сможет сообщить ускорение 2 м/с2?
Ответ: а) m=3 кг; б) m=5 кг; в) m=1,5 кг; г) m=2,5 кг; д) m=1 кг.
 1.1.36. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. С каким ускорением будут двигаться бруски, если к одному из них приложить силу в F=10 Н, направленную горизонтально (рис. 1.22)? Трением пренебречь.
1.1.36. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. С каким ускорением будут двигаться бруски, если к одному из них приложить силу в F=10 Н, направленную горизонтально (рис. 1.22)? Трением пренебречь.
Ответ: а) а=2 м/с2; б) а=0,2 м/с2; в) а=0,02 м/с2; г) а=1,2 м/с2; д) а=3,2 м/с2.
1.1.37. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе (рис. 1.22). Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить ко второму бруску? Трением пренебречь.
Ответ: а) T=12 Н; б) T=3 Н; в) T=13 Н; г) T=5 Н; д) T=2 Н.
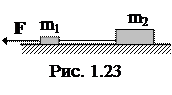 1.1.38. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить к первому бруску (рис. 1.23)? Трением пренебречь.
1.1.38. Два бруска массами m1=1 кг и m2=4 кг, соединенные шнуром, лежат на столе. Какова будет сила натяжения шнура, соединяющего бруски, если силу в F=10 Н приложить к первому бруску (рис. 1.23)? Трением пренебречь.
Ответ: а) T=10 Н; б) T=8 Н; в) T=6 Н; г) T=12 Н; д) T=4 Н.
1.1.39. Автомобиль весит 9,8×103 Н. Во время движения автомобиля по горизонтальной дороге, на него действует сила трения, равная 0,1 его веса. Чему должна быть равна сила тяги, развиваемой двигателем автомобиля, чтобы он двигался равномерно?
Ответ: а) F=98×103 Н; б) F=9,8×103 Н; в) F=0,98×103 Н; г) F= =0,98 Н; д) F=7,8×103 Н.
1.1.40. Автомобиль весит 9,8×103 Н. Во время движения автомобиля по горизонтальной дороге, на него действует сила трения, равная 0,1 его веса. Чему должна быть равна сила тяги, развиваемой двигателем автомобиля, чтобы он двигался с ускорением 2 м/с2?
Ответ: а) F=0,98∙103Н; б) F=1,98∙103Н; в) F=3,98∙103Н; г) F= =2,98∙103 Н; д) F=4,98∙103 Н.
1.1.41. С каким ускорением поднимается лифт, если пружинные весы с гирей в 2 кг в момент начала подъема показали 24 Н? Принять g=10м/с2.
Ответ: а) a=1 м/с2; б) a=2 м/с2; в) a=4 м/с2; г) a=3 м/с2; д) a= =2,5 м/с2.
1.1.42. Тело равномерно скользит по наклонной плоскости с углом a. Чему равен коэффициент трения f?
Ответ: а) f=sina; б) f=cosa; в) f=tga; г) f=ctga;
д) f=sina×cosa.
1.1.43. Две гири с массами m1=1 кг и m2=2 кг соединены нерастяжимой, невесомой нитью, перекинутой через невесомый блок. Найти ускорение, с которым движутся гири (рис. 1.24). Трением в блоке пренебречь. Принять g=9,8 м/с2.
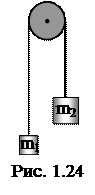 Ответ: а) а=3,27 м/с2; б) а=0,3 м/с2; в) а=9,8 м/с2; г) а=0,98 м/с2; д) а=0,4 м/с2.
Ответ: а) а=3,27 м/с2; б) а=0,3 м/с2; в) а=9,8 м/с2; г) а=0,98 м/с2; д) а=0,4 м/с2.
1.1.44. Две гири с массами 2 кг и 1 кг соединены нерастяжимой, невесомой нитью, перекинутой через невесомый блок (рис. 1.24). Найти силу натяжения нити, действующую на гири. Трением в блоке пренебречь. Принять g=9,8 м/с2.
Ответ: а) Т= 1,31 Н; б) Т= 2,31 Н; в) Т= 23,31 Н;
г) Т= 13,1 Н; д) Т= 3,31 Н.
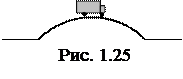 1.1.45. Радиус кривизны выпуклого моста, двигаясь по которому со скоростью 72 км/ч автомобиль не оказывает давления на мост в верхней его точке (рис. 1.25), равен (принять ускорение свободного падения g=10 м/с2):
1.1.45. Радиус кривизны выпуклого моста, двигаясь по которому со скоростью 72 км/ч автомобиль не оказывает давления на мост в верхней его точке (рис. 1.25), равен (принять ускорение свободного падения g=10 м/с2):
Ответ: а) R=50 м; б) R=100 м; в) R=40 м; г) R=120 м; д) R=60 м.
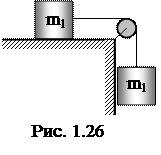 1.1.46. Невесомый блок укреплен на конце стола. Гири равной массы соединены нитью перекинутой через блок (рис. 1.26). Коэффициент трения одной из гирь о стол равен 0,1.1. Найти ускорение, с которым движутся гири. Трением в блоке пренебречь.
1.1.46. Невесомый блок укреплен на конце стола. Гири равной массы соединены нитью перекинутой через блок (рис. 1.26). Коэффициент трения одной из гирь о стол равен 0,1.1. Найти ускорение, с которым движутся гири. Трением в блоке пренебречь.
Ответ: а) а=5,1 м/с2; б) а=7,3 м/с2; в) а=
=9 м/с2; г) а=1,23 м/с2; д) а=4,4 м/с2.
1.1.47. Невесомый блок укреплен на конце стола. Гири равной массы по 1 кг каждая соединены нитью перекинутой через блок. Коэффициент трения одной из гирь о стол равен 0,1 (рис. 1.26). Найти силу натяжения нити. Трением в блоке пренебречь.
Ответ: а) Т=5,4 Н; б) Т=1,8 Н; в) Т=-2,8 Н; г) Т=3,8 Н;
д) Т=2,8 Н.
1.1.48. Маховик радиусом 0,2 м и массой 1 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно 14,7 Н (рис. 1.27). Какое число оборотов в секунду будет делать маховик через 1 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
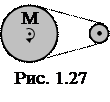 Ответ: а) n=2,67 об/с; б) n=5,67 об/с; в) n= =10,67 об/с; г) n=18,67 об/с; д) n=23,4 об/с.
Ответ: а) n=2,67 об/с; б) n=5,67 об/с; в) n= =10,67 об/с; г) n=18,67 об/с; д) n=23,4 об/с.
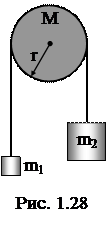 1.1.49. Две гири разного веса соединены нитью, перекинутой через блок, момент инерции которого
1.1.49. Две гири разного веса соединены нитью, перекинутой через блок, момент инерции которого
50 кг×м2 и радиус 0,2 м. Блок вращается с трением и момент сил трения равен 98,1 Н×м (рис. 1.28). Найти разность натяжения нитей по обе стороны блока, если известно, что он вращается с постоянным угловым ускорением 2,36 рад/с2.
Ответ: а) ΔТ=2,68×103 Н; б) ΔТ=5,68×103 Н;
в) ΔТ=1,68×103 Н; г) ΔТ=1,08×103 Н; д) ΔТ=3,68×103 Н.
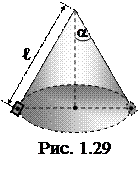 1.1.50. Грузик, подвешенный на нити длиной
1.1.50. Грузик, подвешенный на нити длиной
1 м, (рис. 1.29) движется в горизонтальной плоскости так, что нить, описывающая конус, образует с вертикалью угол 37o. Какое число оборотов в минуту делает грузик?
Ответ: а) n=23,6 об/мин; б) n=33,5 об/мин;
в) n=43,6 об/мин; г) n=53,6 об/мин; д) n=63,6 об/мин.
1.1.51. Грузик массой 120 г, подвешенный на нити длиной 1 м, вращается в горизонтальной плоскости с частотой n=0,56 об/с. Найти силу натяжение нити.
Ответ: а) Т=1,48 Н; б) Т=2,47 Н; в) Т=3,47 Н; г) Т=4,47 Н;
д) Т=5,47 Н.
1.1.52. Груз массой 100 кг, подвешенный на канате, поднимается вертикально вверх ускоренно с ускорением 0,7 м/с2. Определить натяжение каната в этом случае.
Ответ: а) Т=1,5×102 Н; б) Т=2,5×102 Н; в) Т=10,5×102 Н; г) Т= =20,5×102 Н; д) Т=30,5×102 Н.
1.1.53. Груз массой 100 кг, подвешенный на канате, поднимается вертикально вверх равномерно. Определить натяжение каната в этом случае.
Ответ: а) Т=45,8×102 Н; б) Т=25,8×102 Н; в) Т=35,8×102 Н; г) Т= =0,8×102 Н; д) Т=9,8×102 Н.
1.1.54. Груз массой 100 кг, подвешенный на канате, поднимается вертикально вверх замедленно с ускорением 0,8 м/с2. Определить натяжение каната в этом случае.
Ответ: а) Т=9×102 Н; б) Т=10×102 Н; в) Т=20×102 Н; г) Т=30×102 Н; д) Т=40×102 Н.
 1.1.55. На гладком столе лежит брусок массой m=4 кг (рис. 1.30). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти ускорение, с которым движется брусок. Массой блоков и трением пренебречь.
1.1.55. На гладком столе лежит брусок массой m=4 кг (рис. 1.30). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти ускорение, с которым движется брусок. Массой блоков и трением пренебречь.
Ответ: а) а=0,4 м/с2; б) а=1,4 м/с2; в) а=2,4 м/с2; г) а=3,4 м/с2; д) а=4,4 м/с2.
1.1.56. На гладком столе лежит брусок массой m=4 кг (рис. 1.30). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти силу натяжения, действующую на первую гирю. Массой блоков и трением пренебречь.
Ответ: а) Т1=31,2 Н; б) Т1=21,2 Н; в) Т1=11,2 Н; г) Т1=1,12 Н; д) Т1=0,112 Н.
1.1.57. На гладком столе лежит брусок массой m=4 кг (рис. 1.30). К бруску привязаны шнуры, перекинутые через неподвижные блоки. К концам шнуров подвешены гири, массы которых m1=1 кг и m2=2 кг. Найти силу натяжения, действующую на вторую гирю. Массой блоков и трением пренебречь.
Ответ: а) Т=46,8 Н; б) Т=36,8 Н; в) Т=26,8 Н; г) Т=16,8 Н;
д) Т=6,8 Н.
1.1.58. К потолку трамвайного вагона подвешен на нити шар. Вагон тормозит, и его скорость изменяется от 18 км/ч до 6 км/ч за время 3 с. На какой угол отклонится при этом нить с шаром?
Ответ: а) a=36,5о; б) a=26,5о; в) a=16,5о; г) Т=16,8 Н; д) a=6,5о.
1.1.59. Найти силу тяги, развиваемую двигателем автомобиля, движущегося в гору с ускорением 1 м/с2. Уклон горы равен 1 м на каждые 25 м пути. Масса автомобиля 1 т. Коэффициент трения равен 0,1.1.
Ответ: а) Fт=2,37×103 Н; б) Fт=5,37×103 Н; в) Fт=7,37×103 Н;
г) Fт=9,37×103 Н; д) Fт=11,37×103 Н.
 1.1.60. Тело массой 5 кг брошено под углом 30о к горизонту с начальной скоростью 20 м/с (рис. 1.31). Пренебрегая сопротивлением воздуха, найти изменение импульса тела за время полета.
1.1.60. Тело массой 5 кг брошено под углом 30о к горизонту с начальной скоростью 20 м/с (рис. 1.31). Пренебрегая сопротивлением воздуха, найти изменение импульса тела за время полета.
 Ответ: а) Dp=200 (кг×м)/с; б) Dp=100 (кг×м)/с; в) Dp=50 (кг×м)/с;
Ответ: а) Dp=200 (кг×м)/с; б) Dp=100 (кг×м)/с; в) Dp=50 (кг×м)/с;
г) Dp=10 (кг×м)/с; д) Dp=5 (кг×м)/с.
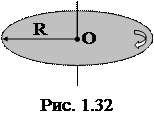
1.1.61. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через центр масс диска перпендикулярно его плоскости (рис. 1.32). Определить величину вращающего момента.
Ответ: а) M=3,25 Н×м; б) M=2,25 Н×м; в) M=1,25 Н×м; г) M= =0,25 Н×м; д) M=0,125 Н×м.
 1.1.62. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с–2 вокруг оси, проходящей через точку расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости (рис. 1.33). Определить величину вращающего момента.
1.1.62. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с–2 вокруг оси, проходящей через точку расположенную на расстоянии l=0,5R от центра масс диска перпендикулярно его плоскости (рис. 1.33). Определить величину вращающего момента.
Ответ: а) M=4,88 Н×м; б) M=3,88 Н×м; в) M=2,88 Н×м; г) M= =1,88 Н×м; д) M=0,88 Н×м.
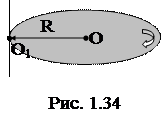 1.1.63. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 1.34). Определить величину вращающего момента.
1.1.63. Диск радиусом R=0,5 м и массой m=2 кг вращается с угловым ускорением 5 с-2 вокруг оси, проходящей через точку расположенную на расстоянии l=R от центра масс диска перпендикулярно его плоскости (рис. 1.34). Определить величину вращающего момента.
Ответ: а) M=0,075 Н×м; б) M=0,75 Н×м; в) M=1,75 Н×м; г) M= =2,75 Н×м; д) M=3,75 Н×м. 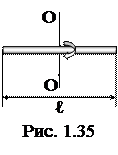
1.1.64. Тонкий стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением e=3 рад/c2 около оси, проходящей через середину стержня перпендикулярно к его длине (рис. 1.35). Определить величину вращающего момента M.
Ответ: а) М=0,025 Н×м; б) М=0,035 Н×м; в) М=0,045 кг×м2/c2;
г) М=0,055 Н×м; д) М=0,065 Н×м.
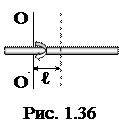 1.1.65. Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии l=0,25 м от середины стержня перпендикулярно к его длине (рис. 1.36). Определить угловое ускорение стержня.
1.1.65. Тонкий стержень длиной 50 см и массой 400 г вращается под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии l=0,25 м от середины стержня перпендикулярно к его длине (рис. 1.36). Определить угловое ускорение стержня.
Ответ: а) e=7 с-2; б) e=6 с-2; в) e=5 с-2; г) e=4 с-2; д) e=3 с-2.
 1.1.66. Тонкий стержень массой 300 г вращается с угловым ускорением e=4 рад/c2 под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии d=0,25 м от середины стержня перпендикулярно к его длине. Определить длину стержня (рис. 1.37).
1.1.66. Тонкий стержень массой 300 г вращается с угловым ускорением e=4 рад/c2 под действием вращающего момента M=0,1 Н×м около оси, проходящей через точку, находящуюся на расстоянии d=0,25 м от середины стержня перпендикулярно к его длине. Определить длину стержня (рис. 1.37).
Ответ: а) l=0,4 м; б) l=0,5 м; в) l=0,6 м; г) l=0,7 м; д) l=0,8 м.
1.1.67. Тонкий стержень длиной 0,5 м под действием вращающего момента M=1 Н×м вращается с угловым ускорением e=3 рад/c2, относительно оси, проходящей через точку, находящуюся на расстоянии d=0,5l (l – длина стержня) от середины стержня перпендикулярно к его длине (рис. 1.37). Определить массу стержня.
Ответ: а) m=2 кг; б) m=3 кг; в) m=4 кг; г) m=5 кг; д) m=6 кг.
1.1.68. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид: j=5+4t2-t3. Какова величина момента сил в момент времени t=2 с.
Ответ: а) M=3,64 Н×м; б) M=-0,64 Н×м; в) M = 0,64 Н×м; г) M= =-2,64 Н×м; д) M -3,64 Н×м.
1.1.69. Шар массой 10 кг и радиусом 20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид: j=5+4t2-t3. Какова величина момента импульса шара в момент времени, равный 2 с.
 Ответ: а) L=3,64 (кг×м2)/с; б) L=-0,64 (кг×м2)/с; в) L=0,64(кг×м2)/с; г) L=-2,64 (кг×м2)/с; д) L=-3,64 (кг×м2)/с.
Ответ: а) L=3,64 (кг×м2)/с; б) L=-0,64 (кг×м2)/с; в) L=0,64(кг×м2)/с; г) L=-2,64 (кг×м2)/с; д) L=-3,64 (кг×м2)/с.
1.1.70. Определить момент инерции шара, массой 10 кг и радиусом 20 см (рис. 1.38), относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=0,56 кг×м2; б) I=0,46 кг×м2; в) I= =0,36 кг×м2; г) I=0,26 кг×м2; д) I=0,16 кг×м2.
1.1.71. Определить момент инерции медного шара радиусом R=10 см относительно оси, расположенной на расстоянии l=0,5R от центра шара.
Ответ: а) I=5,4×10-3 кг×м2; б) I=2,4×10-3 кг×м2; в) I=3,4×10-3 кг×м2; г) I=4,4×10-3 кг×м2; д) I=1,4×10-3 кг×м2.
1.1.72. Определить момент инерции Земли относительно оси вращения.
Ответ: а) I=20,7×1037 кг×м2; б) I=11,7×1037 кг×м2; в) I=9,7×1037 кг×м2; г) I=5,7×1037 кг×м2; д) I=3,7×1037 кг×м2.
1.1.73. Определить момент импульса Земли относительно оси вращения.
Ответ: а) L=17×1033 (кг×м2)/с; б) L=15×1033 (кг×м2)/с; в) L= =12×1033 (кг×м2)/с; г) L=7×1033 (кг×м2)/с; д) L=3×1033 (кг×м2)/с.
 1.1.74. Обруч массой m=1 кг и радиусом
1.1.74. Обруч массой m=1 кг и радиусом
100 см (рис. 1.39) вращается относительно оси, проходящей через центр масс с угловой скоростью 100 рад/с. Определить модуль момента импульса обруча.
Ответ: а) L=150 (кг×м2)/с; б) L=10 (кг×м2)/с; в) L=80 (кг×м2)/с;
г) L=100 (кг×м2)/с; д) L=130 (кг×м2)/с.
 1.1.75. Определить момента инерции обруча, (рис. 1.40) массой m=1 кг и радиусом R=100 см относительно оси, перпендикулярной его плоскости, расположенной на расстоянии l=0,5R от центра.
1.1.75. Определить момента инерции обруча, (рис. 1.40) массой m=1 кг и радиусом R=100 см относительно оси, перпендикулярной его плоскости, расположенной на расстоянии l=0,5R от центра.
 Ответ: а) I=5,25 кг×м2; б) I=4,25 кг×м2;
Ответ: а) I=5,25 кг×м2; б) I=4,25 кг×м2;
в) I=3,25 кг×м2; г) I=2,25 кг×м2; д) I=1,25 кг×м2.
1.1.76. Определить момента инерции алюминиевого цилиндра (рис. 1.41) радиусом R=100см и высотой h=0,5 м относительно оси, перпендикулярной плоскости его оснований, расположенной на расстоянии l=0,5R от центра.
 Ответ: а) I=3,2×103 кг×м2; б) I=4,2×103 кг×м2; в) I=5,2×103 кг×м2; г) I=6,2×103 кг×м2; д) I=7,2×103 кг×м2.
Ответ: а) I=3,2×103 кг×м2; б) I=4,2×103 кг×м2; в) I=5,2×103 кг×м2; г) I=6,2×103 кг×м2; д) I=7,2×103 кг×м2.
1.1.77. Свинцовый цилиндр (рис. 1.42) радиусом 10 см высотой h=0,2 м вращается относительно оси, проходящей через центр масс перпендикулярной основанию цилиндра, с угловой скоростью 100 рад/с. Определить модуль момента импульса такого цилиндра.
Ответ: а) L=1,55 (кг×м2)/с; б) L=15,5 (кг×м2)/с;
в) L=25,5 (кг×м2)/с; г) L=35,5 (кг×м2)/с; д) L=45,5 (кг×м2)/с.
1.1.78. Определить момента инерции алюминиевого цилиндра радиусом R=0,10 м и высотой h=0,50 м относительно оси, перпендикулярной плоскости его оснований, расположенной на расстоянии l=2R от центра (рис. 1.43).
 Ответ: а) I=2,9 кг×м2; б) I=1,9 кг×м2; в) I= =0,9 кг×м2; г) I=0,19 кг×м2; д) I=0,29 кг×м2.
Ответ: а) I=2,9 кг×м2; б) I=1,9 кг×м2; в) I= =0,9 кг×м2; г) I=0,19 кг×м2; д) I=0,29 кг×м2.
1.1.79. Маховое колесо начинает вращаться с угловым ускорением e=0,5 рад/с2 и через время t=15 с после начала движения приобретает момент импульса L=73,5 (кг×м2)/с. Определить момент инерции махового колеса.
Ответ: а) I=9,8 кг×м2; б) I=7,2 кг×м2; в) I=5,8 кг×м2; г) I=6,2 кг×м2; д) I=2,2 кг×м2.
1.1.80. К ободу диска радиусом R=0,1 м приложена касательная сила F=19,6 Н. Какой момент импульса приобретет диск через время t=5 с?
Ответ: а) L=10,8 (кг×м2)/с; б) L=9,8 (кг×м2)/с; в) L=8,8 (кг×м2)/с; г) L=7,8 (кг×м2)/с; д) L=6,8 (кг×м2)/с.
1.1.81. Для гироскопической стабилизации корабля используют в качестве гироскопа однородный круглый диск массой 5×104 кг и радиусом 2 м, который вращается с угловой скоростью 94,2 рад/с. Определить модуль момента импульса стабилизатора.
Ответ: а) L=9,42×106 кг×м2/с; б) L=94,2×106 кг×м2/с; в) L= =0,942×106 кг×м2/с; г) L=1,942×108 кг×м2/с; д) L=2,942×108 кг×м2/с.
1.1.82. Диск радиусом 20 см и массой 7 кг вращается согласно уравнению j=3-t+0,1t3. Определить модуль момента сил в момент времени t=2 с.
Ответ: а) М=0,168 Н×м; б) М=168 Н×м; в) М=17 Н×м; г) М=8 Н×м; д) М=16 Н×м.
1.1.83. Маховик, масса которого m=5 кг равномерно распределена по ободу радиусом r=20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой n=720 об/мин. Найти проекцию тормозящего момента на ось, сонаправленную с угловой скоростью, если маховик останавливается за промежуток времени Dt=20 сек.
Ответ: а) Mт= -0,075 Н×м; б) Mт= -0,0075 Н×м; в) Mт= -75 Н×м; г) Mт= -0,75 Н×м; д) Mт= -7,5 Н×м.
1.1.84. Маховое колесо, имеющее момент инерции 245 кг×м2, вращается, делая 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти численное значение момента сил трения.
Ответ: а) М=313 Н×м; б) М=513 Н×м; в) М=173 Н×м; г) М=
=283 Н×м; д) М=163 Н×м.
1.1.85. Маховое колесо вращается, делая 25 об/с. Через две минуты после того, как на колесо перестал действовать вращающий момент M=513 Н×м, оно остановилось. Найти момент инерции махового колеса.
 Ответ: а) I=592 кг×м2; б) I=492 кг×м2; в) I=392 кг×м2; г) I=
Ответ: а) I=592 кг×м2; б) I=492 кг×м2; в) I=392 кг×м2; г) I=
=292 кг×м2; д) I=192 кг×м2.
1.1.86. На барабан радиусом R=0,5 м намотан шнур, к концу которого привязан груз массой 10 кг (рис. 1.44). Найти момент инерции барабана, если известно, что груз опускается с ускорением a=2,04 м/с2.
Ответ: а) I=9,6 кг×м2; б) I=19,6 кг×м2; в) I=29,6 кг×м2; г) I=39,6 кг×м2; д) I=49,6 кг×м2.
1.1.87. На барабан массой M=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение груза. Барабан считать однородным цилиндром (рис. 1.44). Трением пренебречь.
Ответ: а) a=5 м/с2; б) a=3 м/с2; в) a=1 м/с2; г) a=7 м/с2;
д) a=4 м/с2.
1.1.88. Момент силы, действующий на тело, равен 9,8 Н×м. Через 10 с после начала вращения тело достигло угловой скорости 4 с-1. Найти момент инерции тела.
Ответ: а) I=4,5 кг×м2; б) I=14,5 кг×м2; в) I=24,5 кг×м2; г) I=
=34,5 кг×м2; д) I=44,5 кг×м2.
1.1.89. Сплошной шар массой m=1 кг и радиусом R=5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением: j=4+2t+t2. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу.
Ответ: а) F=0,44 Н; б) F=0,34 Н; в) F=0,24 Н; г) F=0,14 Н;
д) F=0,04 Н.
1.1.90. Сплошной шар массой m=1 кг и радиусом R=5 см вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. После прекращения действия силы шар останавливается. Закон вращения шара выражается уравнением: j=1+4t-5t2. Определить тормозящий момент.
Ответ: а) М=5 Н×м; б) М=37 Н×м; в) М=55 Н×м; г) М=75 Н×м; д) М=100 Н×м.
1.1.91. Материальная точка массой 0,05 кг совершает колебания, уравнение которых имеет вид: x=0,1sin5pt. Найти силу, действующую на точку в момент, когда фаза колебаний равна 30о.
Ответ: а) F=-0,92 Н; б) F= -0,82 Н; в) F= -0,72 Н; г) F= -0,62 Н; д) F=-0,52 Н.
1.1.92. Материальная точка массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид x=0,2sin8pt. Найти численное значение возвращающей силы в момент времени t=0,1с.
Ответ: а) F=0,54 Н; б) F=0,74 Н; в) F=1,4 Н; г) F=0,94 Н;
д) F=0,84 Н.
1.1.93. Точка совершает гармонические колебания, уравнение которых имеет вид x=5sin(3/2)pt. Найти момент времени, когда точка имеет фазу колебаний 0,927 рад.
Ответ: а) t=0,2 с; б) t=0,3 с; в) t=0,4 с; г) t=0,5 с; д) t=0,6 с.
1.1.94. Чему равен период колебаний математического маятника длиной l=1 м, находящегося в трамвайном вагоне, движущемся горизонтально с ускорением a=7 м/с2?
Ответ: а) T=0,8 с; б) T=1,8 с; в) T=2,8 с; г) T=3,8 с; д) T=4,8 с.
1.1.95. Определить период колебаний математического маятника длиной l=1 м в лифте, движущемся вертикально с ускорением a=2 м/с, направленным вверх.
Ответ: а) T=3,83 с; б) T=2,83 с; в) T=1,83 с; г) T=0,83 с;
д) T=0,083 с.
1.1.96. Определить период колебаний математического маятника длиной l=1 м в лифте, который движется вертикально с ускорением a=1,8 м/с2, направленным вниз.
Ответ: а) T=5,2 с; б) T=4,2 с; в) T=3,2 с; г) T=2,2 с; д) T=1,2 с.
1.1.97. Какова длина математического маятника, совершающего колебания по закону x=0,04cos(2t+0,8)?
Ответ: а) l=0,45 м; б) l=1,45 м; в) l=1,95 м; г) l=2,45 м;
д) l=2,95 м.
1.1.98. Один из двух математических маятников совершил за некоторое время n1=6 колебаний, а другой – n2=10 колебаний. Разность длин маятников Dl=16×10-2 м. Найти длины маятников ℓ1 и ℓ2.
Ответ: а) ℓ1=0,25 м, ℓ2=0,09 м; б) ℓ1=0,4 м, ℓ2=0,24 м; в) ℓ1= =0,5 м, ℓ2=0,34 м; г) ℓ1=1,0 м, ℓ2=0,84 м; д) ℓ1=0,6 м; ℓ2=0,44 м.
1.1.99. Найти массу груза, который на пружине с жесткостью
250 Н/м совершает 100 полных колебаний за 80 с.
Ответ: а) m=5 кг; б) m=4 кг; в) m=3 кг; г) m=2 кг; д) m=1 кг.
1.1.100. Уравнение колебаний пружинного маятника массой 200 г имеет вид x=0,05cos(8pt+p/3). Определить жесткость пружины, если ее массой можно пренебречь.
Ответ: а) k=1,26 Н/м; б) k=12,6 Н/м; в) k=126 Н/м; г) k=226 Н/м; д) k=326 Н/м.
1.1.101. К пружине подвешен груз массой 10 кг. Сколько колебаний может совершить этот пружинный маятник за 5 с, если под действием силы 20 Н пружина растягивается на 3 см?
Ответ: а) N=3,5; б) N=4,5; в) N=5,5; г) N=6,5; д) N=7,5.
1.1.102. Стержень длиной 40 см колеблется около оси, перпендикулярной стержню и проходящей через один из его концов. Определить период колебаний такого маятника. Принять g=9,8 м/с2.
Ответ: а) T=0,94 с; б) T=1,04 с; в) T=1,14 с; г) T=1,24 с;
д) T=1,34 с.
1.1.103. Обруч диаметром 56,6 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти частоту этих колебаний. Принять g=9,8 м/с2.
Ответ: а) n=0,96 Гц; б) n=0,76 Гц; в) n=0,66 Гц; г) n=0,56 Гц; д) n=0,46 Гц.
1.1.104. Диск радиусом 10 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний такого физического маятника. Принять g=9,8 м/с2.
Ответ: а) T=0,58 с; б) T=0,68 с; в) T=0,78 с; г) T=0,88 с;
д) T=0,98 с.
1.1.105. Тонкий однородный стержень длиною 60 см колеблется около горизонтальной оси, проходящей через конец стержня. Определить длину математического маятника, период колебаний которого равен периоду колебаний стержня.
Ответ: а) ℓ=1,4 м; б) ℓ=1 м; в) ℓ=0,4 м; г) ℓ=2 м; д) ℓ=0,8 м.
1.1.106. Физический маятник в виде тонкого кольца совершает малые колебания около оси, проходящей через одну из точек кольца перпендикулярно его плоскости. Найти длину математического маятника, обладающего тем же периодом, что и данное кольцо.
Ответ: а) ℓ=2R м; б) ℓ=3R м; в) ℓ=4 Rм; г) ℓ=5R м; д) ℓ=6R м.
1.1.107. Логарифмический декремент затухания маятника l=0,003. Определить число N полных колебаний, которые должен совершить маятник, чтобы амплитуда уменьшилась в два раза.
Ответ: а) N=91; б) N=121; в) N=151; г) N=191; д) N=231.
1.1.108. Чему равен логарифмический декремент колебаний математического маятника, если за 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника равна 1 м.
Ответ: а) l=2,3; б) l=1,3; в) l=0,23; г) l=0,23; д) l=0,023.
1.1.109. За время t=8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания.
Ответ: а) b=0,0023 с-1; б) b=0,023 с-1; в) b=0,23 с-1; г) b=1,23 с-1; д) b=2,23 с-1.1.
1.1.110. Гиря, подвешенная к спиральной пружине, совершает упругие колебания в некоторой среде. Логарифмический декремент затухания l=0,004. Сколько колебаний должна совершить гиря, чтобы амплитуда колебаний уменьшилась в два раза (рис. 1.1.73)?
Ответ: а) N=273; б) N=173; в) N=73; г) N=7,3; д) N=3.
 1.1.111. Гиря, подвешенная к спиральной пружине, совершает упругие колебания в некоторой среде (рис. 1.45). Логарифмический декремент затухания l=0,004. За какое время t произойдет уменьшение амплитуды колебаний в два раза?
1.1.111. Гиря, подвешенная к спиральной пружине, совершает упругие колебания в некоторой среде (рис. 1.45). Логарифмический декремент затухания l=0,004. За какое время t произойдет уменьшение амплитуды колебаний в два раза?
Ответ: а) t=1,72 с; б) t=17,2 с; в) t=172 с; г) t= =272 с; д) t=0,172 с.
1.1.112. Амплитуда затухающих колебаний математического маятника за время t=60 с уменьшилась в два раза. За какое время уменьшится амплитуда колебаний того же маятника в восемь раз?
Ответ: а) t=160 с; б) t=170 с; в) t=180 с; г) t=190 с; д) t=200 с.
1.1.113. По грунтовой дороге, по которой прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l=30 см друг от друга, прокатили детскую коляску. Коляска имеет две одинаковые параллельные рессоры, каждая из которых прогибается на x0=2 см под действием груза массой m0=1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M=10 кг.
Ответ: а) v=1,47 м/с; б) v=0,87 м/с; в) v=0,67 м/с; г) v=0,47 м/с; д) v=0,27 м/с.
1.1.114. Определить длину рельса железнодорожного полотна, если при скорости поезда v=21 м/с рессоры его вагонов особенно сильно совершают колебательные движения под действием толчков колес о стыки рельс. Нагрузка на рессору равна 5,5×103 кг. Рессора прогибается на 16 мм при нагрузке 103 кг.
Ответ: а) l=9,5 м; б) l=21,5 м; в) l=18,5 м; г) l=15,5 м;
д) l=12,5 м.
1.1.115. При какой скорости вагон начнет сильно раскачиваться вследствие толчков на стыках рельс, если длина рельс 25 м? Жесткость пружин рессоры вагона 4,81×105 Н/м. Масса вагона с грузом 64 тонны. Вагон имеет четыре рессоры.
Ответ: а) v=22 м/с; б) v=12 м/с; в) v=2 м/с; г) v=0,22 м/с;
д) v=0,12 м/с.
1.1.116. Определить собственную частоту колебаний моста, по которому запрещается движение взводу солдат, идущих строевым шагом. Длина шага равна 0,8 м. Длина моста 96 м. Предполагаемое время движения солдат по мосту 1 мин.
Ответ: а) n=2 Гц; б) n=1 Гц; в) n=0,5 Гц; г) n=3 Гц; д) n=4 Гц.
1.1.117. Под действием силы тяжести, действующей на электромотор, консольная балка прогнулась на Dx=1 мм. При каком числе оборотов якоря электромотора в минуту может возникнуть опасность резонанса?
Ответ: а) n=746 об/мин; б) n=946 об/мин; в) n=1046 об/мин;
г) n=1146 об/мин; д) n=1246 об/мин.
1.1.118. Во сколько раз циклическая резонансная частота вынужденных колебаний будет больше циклической частоты собственных колебаний системы, при коэффициенте затухания β=0,2w0, где w0 – циклическая частота собственных незатухающих колебаний.
Ответ: а) в 3,96 раза; б) в 2,96 раза; в) в 1,96 раза; г) в 0,96 раза; д) в 0,096 раза.
1.1.119. Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты в два раза? Коэффициенты затухания β принять равным 0,1w0, где w0 – циклическая частота собственных незатухающих колебаний.
Ответ: а) в 14,8 раза; б) в 15,8 раза; в) в 16,8 раза; г) 17,8 раза; д) в 18,8 раза.
1.1.120. При выступлении одного из популярных певцов в зрительном зале неожиданно "зазвененили" стекла окон. Определить собственную циклическую частоту стекол, если коэффициенты затухания β=0,2w0, где w0 – циклическая частота собственных незатухающих колебаний, а частота отклика n=1200 Гц.
Ответ: а) n=826 Гц; б) n=926 Гц; в) n=1026 Гц; г) n=1226 Гц; д) n=1426 Гц.
