Метод гаусса с постолбцовым выбором главного элемента

В основе метода Гаусса лежит поэтапное приведение системы (5.1) к треугольному виду, исключая последовательно сначала 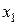из второго, третьего, … -го уравнений, затем из третьего, четвертого, …, -го уравнений преобразованной системы, и т.д.

На первом этапе заменим второе, третье, …, -е уравнения на уравнения, получающиеся сложением этих уравнений с первым, умноженным соответственно на 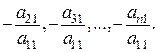Результатом этого этапа преобразований будет эквивалентная (5.1) система

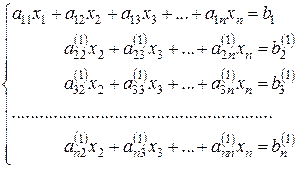(5.2)

коэффициенты которой (с верхним индексом 1) подсчитываются по формулам

, где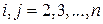

При этом можно считать, что 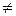0, так как по предположению система (5.1) однозначно разрешима, значит, все коэффициенты при 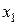не могут одновременно равняться 0, и на первое место всегда можно поставить уравнение с отличным от нуля первым коэффициентом.

На втором этапе проделываем такие же операции, как и на первом, с подсистемой системы (5.2), получающейся исключением первого уравнения. Эквивалентный (5.2) (а значит, и (5.1)) результат второго этапа будет иметь вид

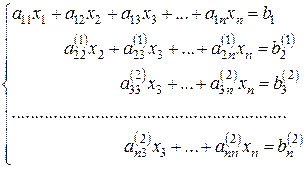
где ; .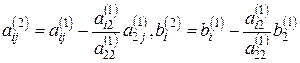

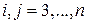Продолжая этот процесс, на (n-1) этапе, так называемого прямого хода метода Гаусса данную систему (5.1) приведем к треугольному виду:

(5.3)

Коэффициенты системы могут быть получены по формулам

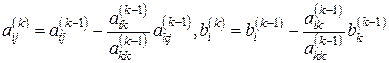, (5.4)

где верхний индекс 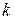(номер этапа) должен изменяться от 1 до 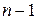, нижние индексы 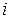и 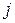(в любой очередности) – от до ; по определению полагаем

.

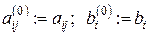Треугольная система (5.3) позволяет последовательно, одно за другим вычислять значения неизвестных, начиная с последнего:

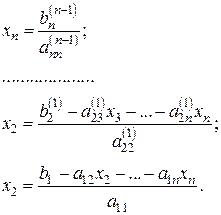
Этот процесс последовательного вычисления значений неизвестных называют обратным ходом метода Гаусса. Он определяется формулой

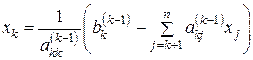, (5.5)

где 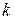полагают равным 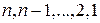и сумма по определению считается равной нулю, если нижний предел суммирования у знака имеет значение больше верхнего.

Итак, решение СЛАУ вида (5.1) методом Гаусса сводится к последовательной реализации вычислений по формулам (5.4) и (5.5).

Учитывая цикличность выполняемых при этом операций, а так же целесообразность хранения промежуточных результатов (пересчитываемых коэффициентов промежуточного этапа), запишем простой алгоритм решения линейных систем (5.1) методом Гаусса:

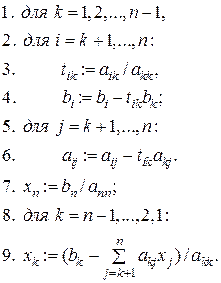
Ошибки округления при выполнении алгебраических операций на каждом шаге метода Гаусса могут привести к достаточно большой погрешности результата. Для уменьшения влияния ошибок округления и исключения деления на нуль в формулах (5.4), на каждом шаге прямого метода переставляют строки подматрицы таким образом, чтобы деление осуществлялось на наибольший по модулю элемент столбца. Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами. Отсюда название рассматриваемой модификации метода, исключающей деление на нуль и уменьшающей вычислительные погрешности, – метод Гаусса с постолбцовым выбором главного элемента (или, иначе, с частичным упорядочиванием по столбцам).

Частичное упорядочивание по столбцам требует внесения в алгоритм следующих изменений: между строками 1и 2 нужно сделать вставку:

«Найти 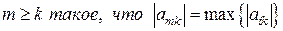; если 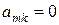, остановить работу алгоритма («однозначного решения нет»), иначе поменять местами 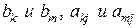при всех » (*)

Более разумным, наверное, является сравнение 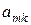не с нулем, а с некоторым малым 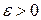, задаваемым вычислителем в зависимости от различных априорных соображений. Счет останавливается или берется под особый контроль, если окажется 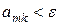. Заметим, что соответствующая частичному упорядочиванию вставка (*) в алгоритм позволяет фактически в процессе его выполнения проводить алгоритмическое исследование системы (5.1) на однозначную разрешимость.

Устойчивость алгоритма к погрешностям исходных данных и результатов промежуточных вычислений можно еще усилить, если выполнять деление на каждом этапе на элемент, наибольший по модулю во всей матрице, преобразуемой на данном этапе подсистемы. Такая модификация метода Гаусса, называемая методом главных элементов, применяется довольно редко, поскольку сильно усложняет алгоритм. Усложнение связано как с необходимостью осуществления двумерного поиска главных элементов, так и с необходимостью запоминать номера столбцов, откуда берутся эти элементы (перестановка столбцов означает как бы переобозначение неизвестных, в связи с чем требуется обратная замена).

Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу 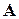системы к треугольному виду (см. (5.3)), таковы, что они не изменяют определителя матрицы 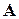. Учитывая, что определитель треугольной матрицы равен произведению диагональных элементов, имеем

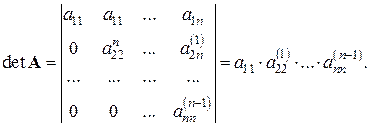
Таким образом, определитель матрицы равен произведению всех ведущих элементов при ее преобразовании методом Гаусса.

При желании получить 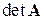дополнительно к решению СЛАУ 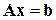алгоритм предыдущего пункта должен быть пополнен всего лишь одной следующей строкой:

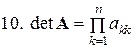
Если метод Гаусса используется только для вычисления определителя, из алгоритма его реализации следует изъять строки 4 и 7-9.

Так как перестановка строк матрицы меняет знак определителя, то при постолбцовом выборе главного элемента, т.е. при включении в алгоритм вставки *, нужно в результате учесть число 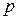произведенных перестановок, точнее, четность этого числа. Это означает, что при вычислении 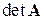алгоритмом Гаусса с частичным упорядочиванием вместо строки 10 должна быть включена строка

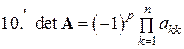
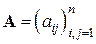Для получения матрицы , обратной к матрице , исходящей из того, что она является решением матричного уравнения

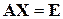, (5.6)

где 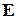– единичная матрица.

Представляя искомую матрицу 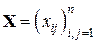как набор (вектор-строку) векторов-столбцов

, , …, ,

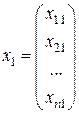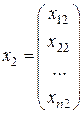а единичную матрицу 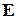как набор единичных векторов

, ,…, ,

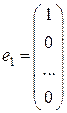матричное уравнение (5.6) в соответствии с правилами умножения матриц подменим эквивалентной системой не связанных между собой векторно-матричных уравнений

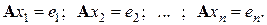(5.7)

Каждое из последних уравнений имеет вид (5.1а) и может быть решено методом Гаусса. При этом специфичным является то обстоятельство, что все СЛАУ (5.7) имеют одну и ту же матрицу коэффициентов, а это означает, что наиболее трудоемкая часть метода Гаусса – приведение матрицы системы к треугольному виду – общая для всех систем (5.7). Так что, если требуется приспособить рассмотренный выше алгоритм решения СЛАУ методом Гаусса к обращению матриц, целесообразно не просто применить его последовательно раз к системам (5.7), а слегка подкорректировать: «размножить» строки 4 и 9 так, чтобы в роли вектора 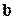оказались все единичные векторы 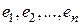. Тогда в результате завершения работы алгоритма будут получаться столбец за столбцом (столбцы «перевернуты»!) элементы обратной матрицы 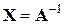. При этом введение в алгоритм частичного упорядочивания, т.е. постолбцовый выбор главного элемента, не требует запоминаний и обратных замен.