Дәріс. Матрицалар және анықтауыштар. Матрицалар

Алғы сөз

Математика қазіргі таңдағы көптеген ғылыми салаларындағы қолданылатын әдістердің теориялық фундаменті болып табылады. Бұл әрине, компьютерлік технологияның онан әрі дамуына байланысты, математиканың қолдану ауқымы кеңейе түсуде.

Курстың мазмұны:сызықтық алгебра және аналитикалық геметрия элементтері. Математикалық анализ: бір айнымалы функцияның дифференциалдық және интегралдық есептеулері.

Курстың мақсаты:студенттерді негізгі математикалық ұғымдарда кезігетін математикалық әдістермен таныстыру. Оқу процесінде кезігетін арнайы курстар мен өз бетінше математиканы қолдану бағытында кезігетін әдістерді игеруге негіз салу.

Курстың міндеттері:жоғары математиканың негізгі ұғымдарын және жер құрылыс саласындағы оны қолдануын оқып білу. Математикалық моделдер туралы түсінік беру және оларды жүзінде қолдана білу.

Студенттер бойында келесі біліктіліктер қалыптасуы керек:бөлінген кредит мөлшерінде өзінің математикалық біліктілігін ұштай отырып, жоғарғы математикадағы оқылатын математикалық ұғымдармен әдістерді жете меңгеріп, өз мамандығында оларды қолдана білетін дәрежеге жетуі тиіс.

Игеруі керек:бір айнымалы функцияның дифференциалдық және интегралдау есептеулерін және меңгеріп, сонымен қатар олардың қолдануларын меңгеру тиіс. Кейбір математикалық моделдерді оқып, олардың қолдану ауқымын білуі тиіс.

Қалыптасатын дағдылары: сабаққа ауқытымен келіп, берілген тапсырмаларды орындап, тиісті балдарын тиянақты түрде тырнақтап жинауды үйрену.

дәріс. Матрицалар және анықтауыштар. Матрицалар

Матрица деп, m- жол және n- бағаннан тұратын сандар немесе әріптерден құрылған тік бұрышты кестені айтады.

Матрица латынның үлкен әріптерімен белгіленеді A,B,C,… және былай жазылады:

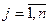немесе қысқаша , мұндағы (яғни ) – жолдың нөмірі, (яғни ) – бағанның нөмірі.

А матрицасын өлшемді матрица дейді және оны деп жазады. Матрицаны құрайтын сандарын сол матрицаның элементтері дейді. элементтері бас диагоналді құрайды. - - өлшемді матрица.

Бір жолдан тұратын матрицаны жол-матрица дейді. Бір бағаннан тұратын матрицаны баған-матрица дейді. Егер матрицаның жолдарының саны бағандарының санына тең болса, ондай матрицаны квадрат матрицадейді. Оның өлшемі болады.

Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.

Егер диагональ матрицаның бас диагоналі бір сандарынан тұрса, онда ондай матрицаны бірлік матрица дейді және оны Е деп белгілейді.

Егер квадрат матрицаның бас диагоналінің бір жағына орналасқан элементтері түгелдей нөлге тең болса, онда оны үшбұрышты матрица дейді.

Егер матрицаның барлық элементтері нөлге тең болса, онда ондай матрицаны

нөлдік матрица дейді. Мысалы. а) квадрат; б) диагональ; в) бірлік; г) нөлдік матрицалар:

а) ; б) ; в) ; г) .

А матрицасының жолдарын сәйкес бағандар етіп алмастырғаннан пайда болған матрицаны транспонирленген матрица деп атайды және оны деп белгілейді. Транспонирлеу амалының қасиеттері:

1-мысал.

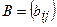Матрицаларға амалдар қолдану.Қосу амалы амалы өлшемдері бірдей матрицалар үшін ғана енгізіледі. Екі және матрицаларының қосындысы деп, элементтері

болатын матрицасын айтады және оны 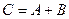деп белгілейді.

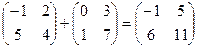
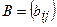2-мысал. матрицасын санына көбейту деп әрбір элементі болатын матрицасын айтады.

3-мысал. -А=(-1)А матрицасын А матрицасына қарама-қарсы матрица деп атайды. Олай болса, матрицалардың айырымын былай анықтауға болады: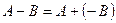

Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері:

мұндағы 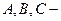матрицалар, 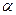және - сандар.

Екі матрицаны көбейту амалы бірінші матрицаның бағандарының саны екінші матрицаның жолдарының санына тең болғанда ғана енгізіледі. 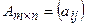матрицасының 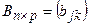матрицасына көбейтіндісі деп элементтері

, ,

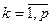
болатын 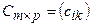матрицасын айтады. Схемалық түрде былай көрсетуге болады:

4-мысал. ,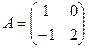

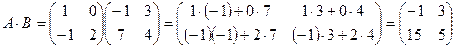
, осыдан

Егер 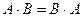болса, онда А және В матрицалары алмастырылатын матрицалар деп аталады.

Матрицаларды көбейту амалының қасиеттері:

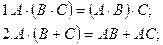
Анықтауыштар.Анықтауыш сатылы түрде анықталады.

1) Кезкелген сан бірінші ретті анықтауыш.

2) Өлшемділігі 2-ге тең квадрат матрица үшін саны (мұндағы - нақты сандар) А матрицасының анықтауышы немесе 2-ші ретті анықтауыш деп аталады және ол 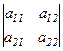, , 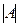, деп белгіленеді. Сонымен

5-мысал.

3) - 3-ші ретті матрица болсын.

А матрицасының анықтауышы немесе 3-ші ретті анықтауышы деп, төменгі формуламен есептелінетін санды айтады:

.

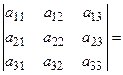
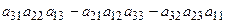Бұл формуланы жеңіл есте сақтау үшін алғашқы оң таңбалы үш қосылғышты 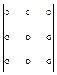схемасы бойынша, ал қалған үш теріс таңбалы қосылғыштарды схемасы бойынша есептелетіндігін ескеру қажет.

4) 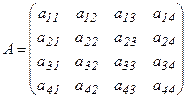квадрат матрицасының элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны 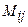деп белгілейді. Ал саны элементінің алгебралық толықтауышы деп аталады. Онда 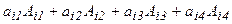саны 4-ші ретті анықтауыш деп аталады және ол 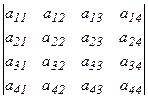түрінде белгіленеді. Дәл осылай 5-ретті анықтауыш анықталады:

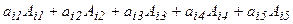(1.1)

Осылайша кезкелген -ші ретті анықтауышты 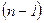-ші ретті анықтауыштар арқылы анықтаймыз.

(1.1) формуласы анықтауышты кез келген жолдың элементтері арқылы жіктеу деп аталады.

6-мысал.

Анықтауыштың қасиеттері:

1. Анықтауыштың жолдарын сәйкес бағандармен алмастырғаннан анықтауыштың мәні өзгермейді.

2. Егер анықтауыштың қандай да бір жолы (бағаны) тек нөлден тұрса, онда анықтауыш нөлге тең.

3.Егер анықтауыштың екі жолы (бағаны) пропорционал болса, онда анықтауыш нөлге тең.

4. Жолдың (бағанның) ортақ көбейткішін анықтауыштың алдына шығарып жазуға болады.

5.Егер анықтауыштың екі жолын (бағанын) алмастырса, онда анықтауыштың таңбасы өзгереді.

6. Егер қандай да бір жолдың (бағанның) элементтеріне кез келген санға көбейтілген басқа жолдың сәйкес элементтерін қосқаннан анықтауыш өзгермейді.

Әдебиеттер: 1 нег.[5-20], 11 қос. [92-115]

Бақылау сұрақтар:

1. Екінші ретті анықтауыш деген не? 4-ретті анықтауыш деген не? Анықтауыштардың

негізгі қасиеттерін атаңыз.

2. Матрицаның анықтауыштан айырмашылығы неде? Матрицаларға қолданылатын амалдарды атаңыз.

3. Екі матрицаны көбейту қай кезде орындалады?