Новая парадигма динамики

Томас Кун в книге «Структура научных революций» утверждает, что крупные изменения происходят в науке в общем не тогда, когда выдвигаются новые теории, а когда меняются простые модели, с помощью которых ученые формулируют и осваивают теорию. Концептуальная модель или задача, которая охватывает основные свойства целого класса задач, названа им «парадигмой». Модель, состоящая из массы и пружины, является такой парадигмой теории колебаний. В области нелинейной динамики классическими парадигмами стали движение маятника и задача трех тел небесной механики.

Нет лучшего примера теории, новые модели и парадигмы которой обещают значительные перемены в естественнонаучном и математическом мышлении, чем нелинейная динамика, испытывающая сейчас революционные изменения. Двумя главными парадигмами здесь являются аттрактор Лоренца и логистическое уравнение. Эти два примера заключают в себе многие особенности хаотической динамики, такие, как разбегающиеся траектории, субгармонические бифуркации, удвоение периода, отображения Пуанкаре и фрактальные размерности. Как для освоения теории линейных колебаний необходимо изучить все тонкости модели из массы с пружиной, без которых нельзя понять колебания сложных систем. Каждому, кто ищет свой путь в современной нелинейной динамике, не обойтись без понимания явлений, скрытых в модели Лоренца и логистическом уравнении. Другие, менее яркие парадигмы также важны для понимания и развития теории динамических систем. Среди них вынужденные движения осциллятора Ван дер Поля, модели осциллятора Дуффинга, разработанные Уэдой и Холмсом.

Математические модели хаотических физических систем. Мы будем отличать математические модели, построенные для физических процессов с хаотической динамикой, и физические эксперименты, в которых непосредственно наблюдаются хаотические движения. Читатели, имеющие в распоряжении небольшой компьютер, могут наблюдать хаотические решения для многих из этих моделей с помощью численного интегрирования методом Рунге-Кутта.

Тепловая конвекция в жидкости. По-видимому, самой знаменитой сейчас моделью является система Лоренца, которая возникла в результате попытки моделирования динамики атмосферы. Представим себе слой жидкости, находящийся под действием силы тяготения, который подогревается снизу, так что поперек слоя поддерживается разность температур (см. рисунок). Когда эта разность становится достаточно большой, возникают циркуляционные, подобные вихрям, движения жидкости, в которых теплый воздух (жидкость) поднимается, а холодный – опускается. Верхушки параллельных рядов конвективных валов можно иногда увидеть, пролетая над слоем облаков. Двумерное конвективное течение можно описать с помощью классического уравнения Навье-Стокса. Это уравнение раскладывается по фурье-гармоникам вдоль двух пространственных направлений, а на поверхности и на дне слоя жидкости задаются граничные условия. При малых разностях температур жидкость неподвижна, но при некотором критическом значении возникает конвективное, т.е. циркуляционное течение. Это движение называют конвекцией Рзле-Бенара.

Рисунок 1.71 - Тепловая конвекция а – схематическое изображение конвективных валов в подогреваемой снизу жидкости; б – три неустойчивые сингулярные точки в фазовом пространстве уравнений Лоренца

Лоренц изучал разложения Фурье, в которых оставлено всего три гармоники. При принятых упрощениях скорость жидкости следующим образом выражается через функцию тока :

.

В модели Лоренца безразмерные функции тока и возмущенная температура записываются в виде

,

где толщина слоя жидкости принята равной единице. В результате получаются следующие уравнения для :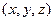

,

Параметр – безразмерное отношение коэффициентов вязкости и теплопроводности (число Прандтля), – безразмерный градиент температуры (связанный с числом Рэлея), a – геометрический множитель, причем (рисунок 1.72)

Рисунок 1.72 - Траектория, отвечающая хаотическому решению уравнений Лоренца для тепловой конвекции жидкости, по результатам численного моделирования

При наборе параметров 10, 28 и 8/3 (использованном Лоренцем) имеются три точки равновесия, и все они неустойчивы. В начале координат расположена седловая точка, а две другие – неустойчивые фокусы, т.е. спиральные точки равновесия. Тем не менее, можно показать, что движение глобально ограничено. Поэтому траекториям не остается ничего другого, кроме как оставаться внутри эллипсоидальной области в фазовом пространстве. Пример таких блуждающих траекторий, полученный при численных расчетах, показан на рисунке.

Траектория, отвечающая хаотическому решению уравнений Лоренца для конвекции жидкости, по результатам численного моделирования.

Часто случается, что важные открытия делаются не одним исследователем – несколько человек в разных местах примерно одновременно обнаруживают новое явление. Так случилось и с моделями динамики тепловой конвекции, имеющими небольшое число степеней свободы. Выше мы обсудили ныне знаменитые уравнения Лоренца, которые через некоторое время после их получения вызвали громадный интерес математиков. Но примерно в то же время Мур и Шпигель, сотрудники соответственно Института им. Годдарда и Нью-йоркского университета, предложили модель неустойчивых колебаний жидкости, которая вращается, содержит магнитное поле или является сжимаемой и в которой присутствует тепловая диссипация. Как и уравнения Лоренца, полученные в их статье уравнения эквивалентны трем дифференциальным уравнениям первого порядка.

Пусть через обозначено вертикальное смещение массы сжимаемой жидкости в горизонтально стратифицированной среде. Силами, восстанавливающими исходное состояние, являются упругость пружины и сила плавучести, которая возникает благодаря тяготению. Кроме того, жидкий элемент может обмениваться теплом с окружающей средой.

Динамика модели описывается связанными уравнением второго порядка (закон Ньютона) и уравнением переноса тепла, имеющим первый порядок. В результате возникает уравнение третьего порядка. В безразмерном виде оно записывается как

,

где использовано предположение о нелинейном профиле температуры вида

.

Уравнение можно привести к виду

В уравнени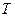и и – безразмерные комплексы, имеющие следующий физический смысл:

,

При численном исследовании этого уравнения обнаружили целую область апериодического движения, показанную на рисунке. Исследовали устойчивость периодических решений в апериодическом режиме (рисунок 1.73).

Рисунок 1.73 - Система из пружины и массы (аналог модели тепловой конвекции); б – область непериодических движений в пространстве безразмерных параметров модели тепловой конвекции

Предел соответствует случаю нулевой диссипации. Как показали Бейкер и др., в этом предельном случае больших периодические решения в области периодических движений становятся локально неустойчивыми. Это сочетание глобальной устойчивости и локальной неустойчивости, по-видимому, характерно для хаотических дифференциальных уравнений. В более поздней работе изучен более общий класс уравнений третьего порядка вида

где имеет смысл потенциальной энергии.

Приведенная система уравнений описывает также осциллятор второго порядка с управляющей обратной связью (параметр ).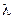

Историков науки ждет интересная задача понять, почему системе Лоренца посвящено так много исследований, а модель Мура – Шпигеля практически игнорируется математиками. В обеих работах моделируется конвекция. Лоренц опубликовал свою статью в Journal of Atmospheric Sciences, а Мур и Шпигель – в Astrophysical Journal.