Дифференцируемость функции многих переменных. частные производные
Пусть  определена в некоторой окрестности точки
определена в некоторой окрестности точки  ,
, 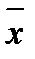 - точка из этой окрестности.
- точка из этой окрестности.
Определение. Величина 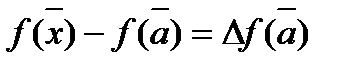 называется приращением функции
называется приращением функции  в точке,
в точке,  соответствующим приращению аргумента
соответствующим приращению аргумента 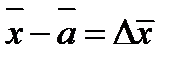 .
.
Определение .Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если существуют такие постоянные числа
, если существуют такие постоянные числа  и функции
и функции 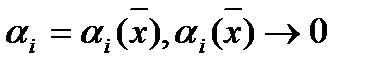 при
при 
 (18.1)
(18.1)
Часто обозначают  и
и 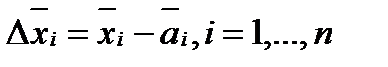 . Тогда перепишем в виде
. Тогда перепишем в виде  .
.
При 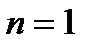 наше определение совпадает с известными определением дифференцируемости
наше определение совпадает с известными определением дифференцируемости  . Для функций одной переменной дифференцируемость равносильна существованию производной. В случае нескольких переменных ситуация несколько сложнее.
. Для функций одной переменной дифференцируемость равносильна существованию производной. В случае нескольких переменных ситуация несколько сложнее.
Сначала введем в рассмотрение величину  . Она представляет собой приращение функции при фиксированных значениях всех производных, кроме i-той.
. Она представляет собой приращение функции при фиксированных значениях всех производных, кроме i-той.
Пусть  дифференцируема в точке
дифференцируема в точке  . Тогда для любого
. Тогда для любого 
 при
при 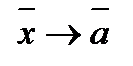
Поскольку 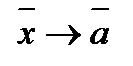 при фиксированных значениях
при фиксированных значениях  равносильно тому, что
равносильно тому, что 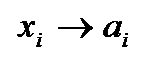 , равенство означает, что функция одной переменной
, равенство означает, что функция одной переменной  .
.
 дифференцируема в точке
дифференцируема в точке 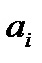 и, значит, существует
и, значит, существует

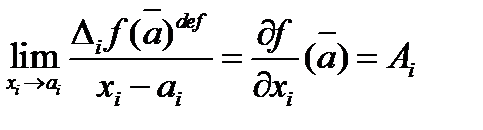
называемый, по определению, частной производной функции  по переменной
по переменной  в точке
в точке  .
.
Мы только что, тем самым, доказали теорему:
Теорема. Если  дифференцируема в точке
дифференцируема в точке  , то для всех
, то для всех  существуют
существуют 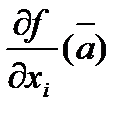 .
.
Таким образом, существование частных производных – необходимое условие дифференцируемости. При этом 
 при
при 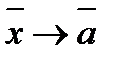 .
.
Другое необходимое условие дифференцируемости – непрерывность функции, как показывает следующая теорема.
Теорема. Если  дифференцируема в точке
дифференцируема в точке  , то
, то  .
.
Однако, в отличие от случая  , из существования частных производных
, из существования частных производных 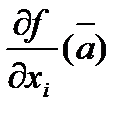 , не следует даже непрерывность функции
, не следует даже непрерывность функции  в точке
в точке  и тем более не следует дифференцируемость
и тем более не следует дифференцируемость  в точке
в точке  .
.
Пример. 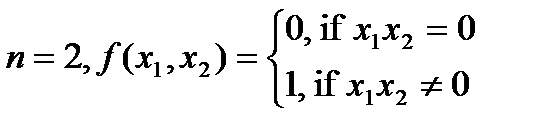 . Тогда
. Тогда 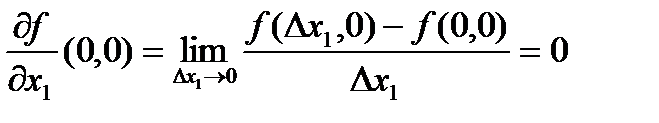 , так как
, так как 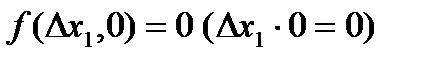 . Аналогично,
. Аналогично, 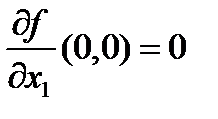 . Однако
. Однако 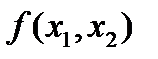 даже не непрерывна в точке
даже не непрерывна в точке  .
.
Достаточное условие дифференцируемости дает следующая теорема.
Теорема. Пусть частные производные 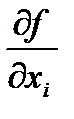 существуют в окрестности точки
существуют в окрестности точки  и непрерывны в этой точке. Тогда
и непрерывны в этой точке. Тогда  дифференцируема в точке
дифференцируема в точке  .
.
Замечание. Непрерывность частных производных не является необходимым условием дифференцируемости функций. Например можно доказать, что функция  дифференцируема в точке
дифференцируема в точке  , но частные производные в этой точке не непрерывны.
, но частные производные в этой точке не непрерывны.
Замечание. Тем не менее, для функции 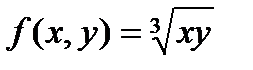 частные производные в точке
частные производные в точке  равны 0, так как
равны 0, так как  и
и  (в остальных точках
(в остальных точках 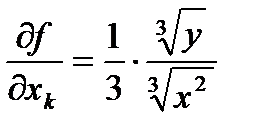 ,
, 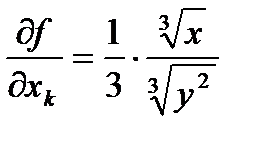 и ясно, что эти производные терпят разрыв в точке
и ясно, что эти производные терпят разрыв в точке  . Но при1ращение
. Но при1ращение 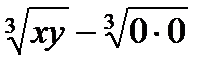 не имеет вид
не имеет вид  , где
, где  при
при  . Действительно, полагая
. Действительно, полагая 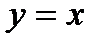 и предполагая, что
и предполагая, что  получаем
получаем  , или
, или  что невозможно, так как при
что невозможно, так как при 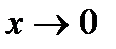 правая часть стремится к 0, а левая нет!
правая часть стремится к 0, а левая нет!
Пусть  определена в некоторой окрестности точки
определена в некоторой окрестности точки 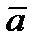 , и пусть в этой точке существуют
, и пусть в этой точке существуют 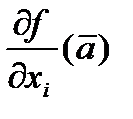 ,
, 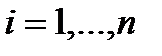 .
.
Определение.Линейная функция от 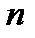 независимых переменных
независимых переменных  вида
вида
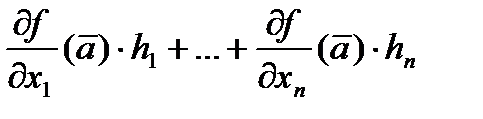 называется дифференциалом
называется дифференциалом 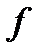 в точке
в точке 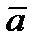 и обозначается
и обозначается  .
.
Каждую из независимых переменных  ,
,  можно рассматривать как функцию
можно рассматривать как функцию  , причем
, причем 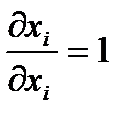 ,
,  , а для любого
, а для любого 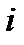 и любого
и любого 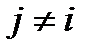 имеем
имеем  .
.
Тогда, последовательно выбирая 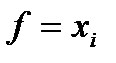 ,
,  , получаем
, получаем
 .
.
Подставляя вместо  величину
величину  , получаем более часто употребляемую запись дифференциала:
, получаем более часто употребляемую запись дифференциала:
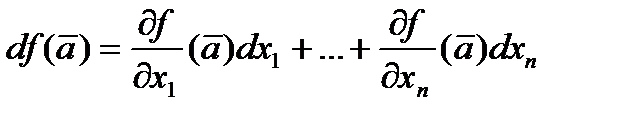 .
.
Обычно величинам переменных  придают значения
придают значения 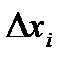 приращений независимых переменных, не входящих при добавлении
приращений независимых переменных, не входящих при добавлении 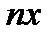 к рассматриваемой точке за границу рассматриваемой области. Независимость переменных
к рассматриваемой точке за границу рассматриваемой области. Независимость переменных 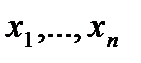 означает, что если взять какое-то приращение
означает, что если взять какое-то приращение 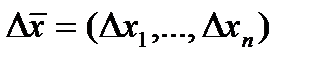 , то оно не меняется при переходе от одной точки области к другой (а для зависимых переменных переход к другой точке вызывает соответствующие изменения вектора
, то оно не меняется при переходе от одной точки области к другой (а для зависимых переменных переход к другой точке вызывает соответствующие изменения вектора 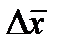 ).
).
Поэтому
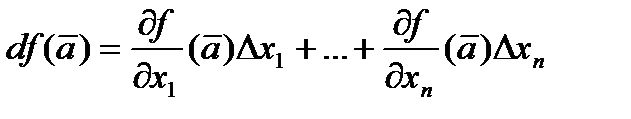 для независимых переменных
для независимых переменных 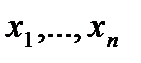 (для них, напомним еще раз,
(для них, напомним еще раз, 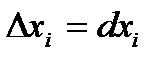 ).
).
Вспомним определение дифференцируемой функции: ее приращение имело вид
 ,
,
где  при
при 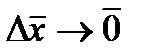 .
.
Это равенство можно переписать в виде
 .
.
Оно означает, что если среди чисел  есть отличное от нуля, то
есть отличное от нуля, то  представляет собой главную, притом линейную по
представляет собой главную, притом линейную по  , часть приращения.
, часть приращения.
Определим (пока формально) вектор 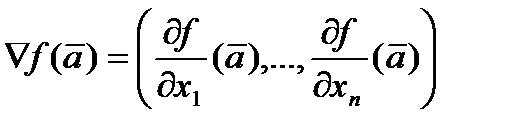 . Тогда
. Тогда  (скалярное произведение). (Вектор градиента служит обобщением понятия производной функции. Напомним, что
(скалярное произведение). (Вектор градиента служит обобщением понятия производной функции. Напомним, что  .)
.)
Для отображения  пространства
пространства 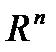 в
в 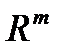 , состоящего из дифференцируемых функций, также можно определить дифференциал
, состоящего из дифференцируемых функций, также можно определить дифференциал  . При этом
. При этом
 .
.
Матрица 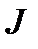 называется матрицей Якоби отображения
называется матрицей Якоби отображения 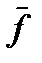 .
.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ. ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
Допустим, что  дифференцируемая в точке
дифференцируемая в точке  функция,
функция,  и
и 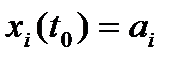 , причем
, причем 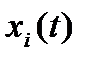 – дифференцируемые в точке
– дифференцируемые в точке  функции. Положим
функции. Положим 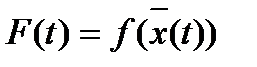 . Тогда
. Тогда 


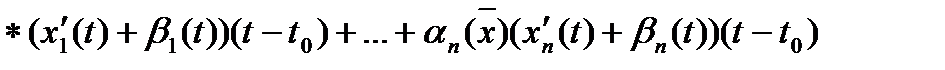 , где
, где  при
при  .
.
В определении дифференцируемости можно доопределить функции 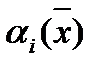 в точке
в точке  , положив
, положив 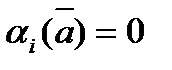 . Тогда при
. Тогда при 
 (а может быть, и принимает значения
(а может быть, и принимает значения  ). Но тогда
). Но тогда 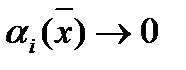 (так как
(так как 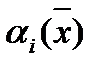 у нас доопределены в точке
у нас доопределены в точке  нулем) и
нулем) и 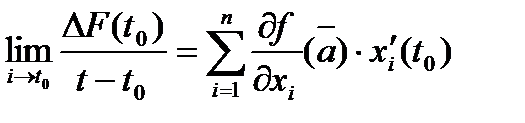 , таким образом,
, таким образом, 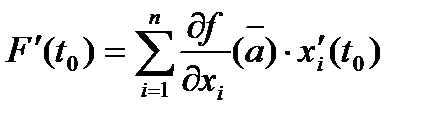 Рассмотрим теперь случай, когда
Рассмотрим теперь случай, когда  . Применяя полученное выше правило, получим, в очевидных обозначениях
. Применяя полученное выше правило, получим, в очевидных обозначениях 
Эти равенства дают правилавычисления производных сложных функций.
Следствие. Следствием этих правил является инвариантность формы первого дифференциала. Именно, пусть 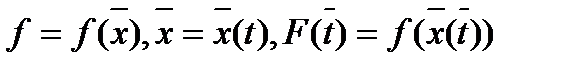 . Тогда
. Тогда 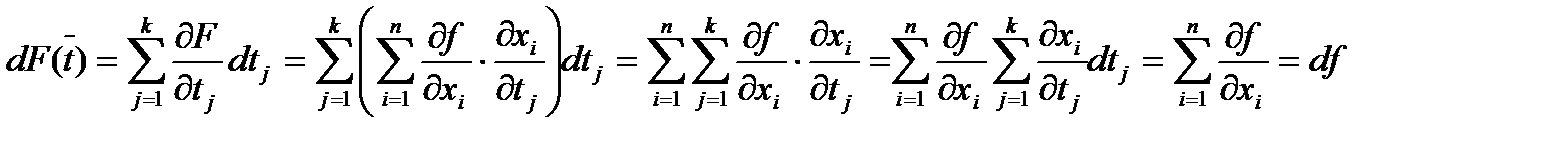 .
.
Это означает, что как в случае независимых переменных 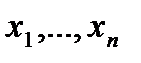 , так и в случае зависимых переменных
, так и в случае зависимых переменных 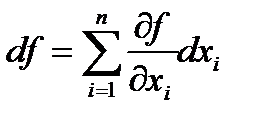 .
.
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
По аналогии с одномерным случаем (прямая называется касательной к кривой в точке 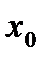 , если расстояние от точки
, если расстояние от точки 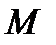 до этой прямой представляет собой бесконечно малую более высокого порядка, чем
до этой прямой представляет собой бесконечно малую более высокого порядка, чем  при
при 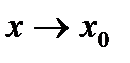 . При этом касательная имеет уравнение
. При этом касательная имеет уравнение 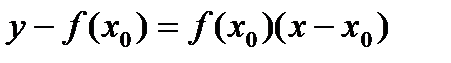 ) будем называть плоскость касательной к поверхностив точке
) будем называть плоскость касательной к поверхностив точке 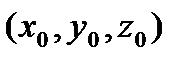 , если расстояние от точки
, если расстояние от точки 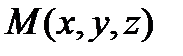 до этой плоскости есть бесконечно малая более высокого порядка, чем
до этой плоскости есть бесконечно малая более высокого порядка, чем 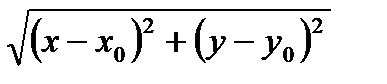 при
при 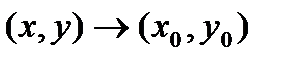 .
.
Пусть 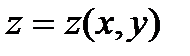 дифференцируема в точке
дифференцируема в точке 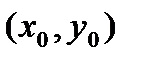 . Существует касательная плоскость к этой поверхности в точке
. Существует касательная плоскость к этой поверхности в точке  и она задается уравнением
и она задается уравнением 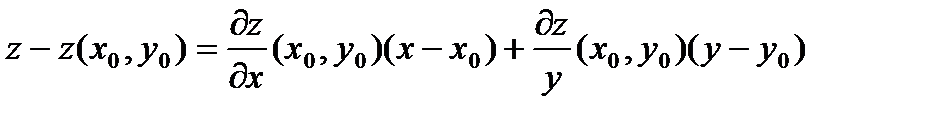 .
.
