Первичная обработка данных
ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Лабораторная работа № 1
ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ
При проведении экспериментов фиксировались значения случайной величины X, характеризующей время простоя оборудования в ожидании ремонта (в часах).
Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.
1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.
Таблица 1 – Расчетная таблица
| Номер п/п | Выборка, час. | Вариацион-ный ряд, 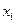 , час. , час. | 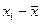 | 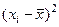 | 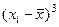 | 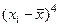 |
| 6,72 | 0,21 | -5,068 | 25,684 | -130,163 | 659,6524 | |
| 8,2 | 0,4 | -4,885 | 23,864 | -116,58 | 569,5061 | |
| 0,4 | 0,64 | -4,642 | 21,55 | -100,036 | 464,3845 | |
| 12,9 | 0,69 | -4,595 | 21,118 | -97,0476 | 445,9774 | |
| 3,15 | 0,77 | -4,509 | 20,33 | -91,6644 | 413,3022 | |
| 34,5 | 0,93 | -4,346 | 18,892 | -82,1113 | 356,8922 | |
| 4,71 | 1,14 | -4,142 | 17,158 | -71,0714 | 294,3925 | |
| 1,14 | 1,51 | -3,772 | 14,226 | -53,6592 | 202,3917 | |
| 2,87 | 1,73 | -3,55 | 12,601 | -44,7323 | 158,7918 | |
| 3,07 | 1,86 | -3,422 | 11,709 | -40,0658 | 137,0981 | |
| 5,86 | -3,277 | 10,741 | -35,2003 | 115,3619 | ||
| 11,4 | 2,1 | -3,179 | 10,105 | -32,1227 | 102,1135 | |
| 3,12 | 2,32 | -2,964 | 8,7873 | -26,0485 | 77,21641 | |
| 0,21 | 2,32 | -2,961 | 8,7695 | -25,9695 | 76,9043 | |
| 1,51 | 2,4 | -2,885 | 8,3222 | -24,0079 | 69,25838 | |
| 2,76 | 2,76 | -2,521 | 6,3562 | -16,025 | 40,40161 | |
| 0,93 | 2,87 | -2,414 | 5,8281 | -14,0699 | 33,96675 | |
| 2,4 | 2,87 | -2,409 | 5,8055 | -13,988 | 33,70356 | |
| 3,5 | 2,99 | -2,294 | 5,2642 | -12,0781 | 27,71187 | |
| 5,29 | 3,07 | -2,214 | 4,9038 | -10,8593 | 24,0474 | |
| 1,86 | 3,12 | -2,163 | 4,6803 | -10,1253 | 21,90503 | |
| 4,99 | 3,15 | -2,132 | 4,5437 | -9,68547 | 20,6456 | |
| 8,77 | 3,5 | -1,776 | 3,1546 | -5,60301 | 9,951645 | |
| 1,73 | 3,6 | -1,683 | 2,8313 | -4,76407 | 8,016242 | |
| 0,77 | 4,59 | -0,691 | 0,477 | -0,32948 | 0,227561 | |
| 5,99 | 4,61 | -0,669 | 0,4478 | -0,29968 | 0,200545 | |
| 7,95 | 4,71 | -0,568 | 0,323 | -0,18359 | 0,104347 | |
| 2,87 | 4,99 | -0,292 | 0,0854 | -0,02497 | 0,007299 | |
| 0,64 | 5,29 | 0,006 | 0,000036 | 0,0000002 | 1,66 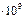 | |
| 5,74 | 5,74 | 0,459 | 0,2103 | 0,096434 | 0,044222 | |
| 0,69 | 5,86 | 0,582 | 0,3384 | 0,196888 | 0,11454 | |
| 2,99 | 5,99 | 0,707 | 0,5003 | 0,35391 | 0,250336 | |
| 4,59 | 6,72 | 1,439 | 2,0704 | 2,978986 | 4,286387 | |
| 2,32 | 7,95 | 2,671 | 7,1361 | 19,06293 | 50,92364 | |
| 2,32 | 8,2 | 2,924 | 8,55 | 25,00068 | 73,10309 | |
| 8,77 | 3,492 | 12,193 | 42,57744 | 148,6755 | ||
| 2,1 | 11,4 | 6,097 | 37,173 | 226,6467 | 1381,866 | |
| 4,61 | 12,9 | 7,608 | 57,874 | 440,2776 | 3349,414 | |
| 30,1 | 30,1 | 24,78 | 614,27 | 15224,23 | 377323,6 | |
| 3,6 | 34,5 | 29,26 | 855,97 | 25043,19 | 732688,6 | |
| Итого | 1874,8 | 39956,09 |
2) Найдем размах выборки 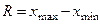 = 34,5- 0,21 = 34,29.
= 34,5- 0,21 = 34,29.
3) Длина интервала 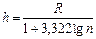 =
= 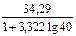 =
= 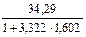 = 5,424.
= 5,424.
4) границы интервалов: 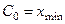 = 0,21,
= 0,21, 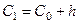 =0,21+5,424 = 5,634,
=0,21+5,424 = 5,634, 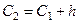 = 5,634 +5,424 = 11,058,
= 5,634 +5,424 = 11,058,
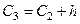 = 11,058 +5,424= 16,482,
= 11,058 +5,424= 16,482, 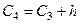 = 16,482+ 5,424= 21,906,
= 16,482+ 5,424= 21,906, 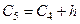 = 21,906+ 5,424 = 27,33,
= 21,906+ 5,424 = 27,33,
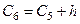 = 27,33+ 5,424 = 32,754,
= 27,33+ 5,424 = 32,754, 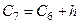 = 32,754+ 5,424 = 38,178
= 32,754+ 5,424 = 38,178 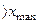 .
.
5) Построим интервальный статистический ряд:
Таблица 2 – Интервальный статистический ряд
Границы интервалов 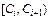 , час. , час. | Частоты 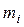 | Частости 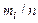 | Накопленные частости |
| [0.21; 5,634) | 29/40 | 29/40 | |
| [5,634; 11,058) | 7/40 | 36/40 | |
| [11,058; 16,482) | 2/40 | 38/40 | |
| [16,482; 21,906) | 0/40 | 38/40 | |
| [21,906; 27,33) | 0/40 | 38/40 | |
| [27,33; 32,754) | 1/40 | 39/40 | |
| [32,754; 38,178) | 1/40 | ||
| Итого |
6) Вычислим числовые характеристики.
В качестве оценки математического ожидания используется среднее арифметическое 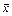 наблюденных значений. Эта статистика называется выборочным средним.
наблюденных значений. Эта статистика называется выборочным средним.
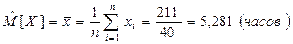 .
.
Для оценивания по выборочным данным моды распределения, используется то значение сгруппированного статистического ряда 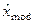 , которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться среднее значение этого интервала.
, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться среднее значение этого интервала.
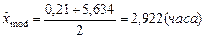 .
.
Для определения выборочного значения медианы используется вариационный ряд. В качестве оценки медианы 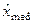 принимают средний (т. е.
принимают средний (т. е. 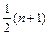 -й) член этого ряда, если значение n – нечётно и среднее арифметическое между двумя средними (т. е. между
-й) член этого ряда, если значение n – нечётно и среднее арифметическое между двумя средними (т. е. между 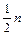 -м и
-м и 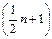 -м) членами этого ряда, если n – чётно. В нашем случае объем выборки
-м) членами этого ряда, если n – чётно. В нашем случае объем выборки 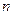 = 40 - четное, т.е. в качестве оценки медианы примем
= 40 - четное, т.е. в качестве оценки медианы примем
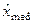 =
= 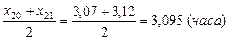 .
.
В качестве оценки дисперсии используется статистика 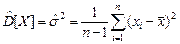 =
= 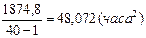 .
.
Оценка среднего квадратического отклонения 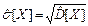 =
= 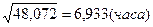 .
.
Оценка коэффициента вариации 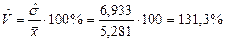 .
.
Оценка коэффициента асимметрии
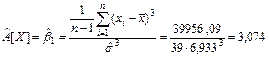 .
.
Оценка коэффициента эксцесса
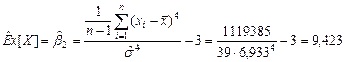 .
.
7) Для приближённого построения эмпирической функции распределения воспользуемся соотношением:
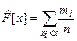
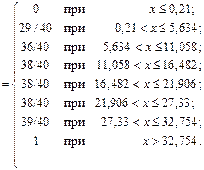
8) Построим гистограмму частот и эмпирическую функцию распределения.
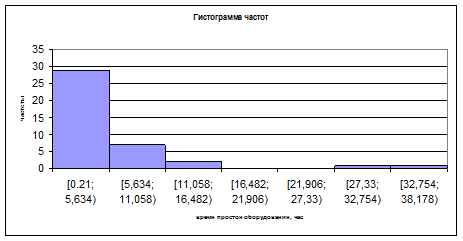
Рисунок 1 – Гистограмма частот
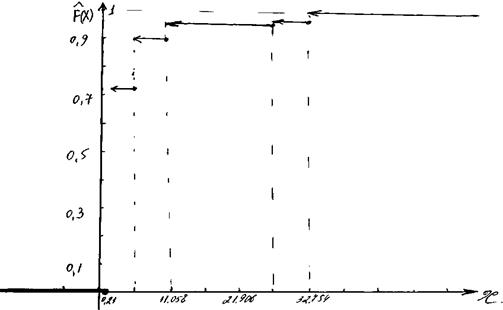
Рисунок 2 – Функция распределения
Вывод. В результате исследования выборки значений непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, получили следующие результаты, час: минимальное время простоя – 0,21, максимальное – 34,54, среднее значение времени простоя оборудования – 5,28, наиболее вероятное время простоя оборудования – 2,922, средневероятное – 3,095, среднеквадратическое отклонение времени простоя оборудования от среднего значения составило 6,933. Оценка коэффициента вариации составила 131,3%, что указывает на большую колеблемость признака относительно среднего значения, оценка коэффициента асимметрии составила 3,074, оценка коэффициента эксцесса составила 9,423.
Лабораторная работа № 2
Подбор закона распределения
одномерной случайной величины
Цель работы: изучить методику применения критерия 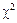 Пирсона для проверки гипотезы о виде закона распределения случайной величины.
Пирсона для проверки гипотезы о виде закона распределения случайной величины.
Задание:с помощью критерия 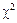 проверить согласование выдвинутой гипотезы о виде закона распределения исследуемой случайной величины с имеющимися выборочными данными.
проверить согласование выдвинутой гипотезы о виде закона распределения исследуемой случайной величины с имеющимися выборочными данными.
Алгоритм применения критерия c2 для проверки гипотезы о виде
закона распределения исследуемой случайной величины.
1 Выборочные данные представляются в виде интервального или сгруппированного статистического ряда.
2 Выбирается уровень значимости a.
3 Формулируется гипотеза о виде закона распределения исследуемой случайной величины.
4 Вычисляются вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения: 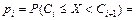
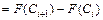 , (
, ( 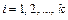 ), где F(x) –гипотетическая функция распределения случайной величины X.
), где F(x) –гипотетическая функция распределения случайной величины X.
Замечание. Если изучается непрерывная случайная величина, то при вычислении значений 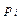 необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:
необходимо изменить границы первого и последнего частичных интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:
| Вид закона распределения | Первый интервал разбиения | Последний интервал разбиения |
| Равномерный | 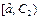 | 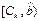 |
| Экспоненциальный | 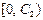 | 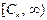 |
| Нормальный | 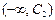 | 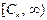 |
5 Определяются значения теоретических частот npi (i = 1, 2,…, k). При необходимости для обеспечения условия npi ³ 3 (если объем выборки 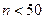 ) , npi ³ 5 (если объем выборки
) , npi ³ 5 (если объем выборки 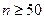 ) , объединяются несколько соседних разрядов разбиения.
) , объединяются несколько соседних разрядов разбиения.
6 Вычисляется наблюдаемое значение критерия c2: 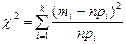 .
.
7 По таблицам квантилей распределения c2 определяется критическое значение 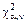 , соответствующее заданному уровню значимости a и числу степеней свободы n = k – r – 1.
, соответствующее заданному уровню значимости a и числу степеней свободы n = k – r – 1.
Если расчётное значение критерия попадает в критическую область, т. е. 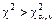 , то проверяемая гипотеза отвергается (при этом вероятность отклонения верной гипотезы равна a).
, то проверяемая гипотеза отвергается (при этом вероятность отклонения верной гипотезы равна a).
В случаях, когда наблюденное значение c2 не превышает критического 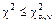 , считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и, в общем случае, не является доказательством истинности этой гипотезы.
, считают, что выдвинутая гипотеза не противоречит опытным данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и, в общем случае, не является доказательством истинности этой гипотезы.
Пример 2.1. По таблице, полученной в лабораторной работе №1 и по гистограмме частот выдвигаем нулевую гипотезу о виде закона распределения случайной величины 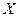 (времени простоя оборудования в ожидании ремонта).
(времени простоя оборудования в ожидании ремонта).
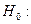 Случайная величина
Случайная величина 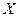 (время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.
(время простоя оборудования в ожидании ремонта) распределена по показательному (экспоненциальному) закону.
Выбираем уровень значимости 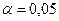 .
.
Вычислим вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения по формуле: 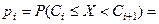
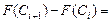
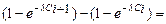 =
= 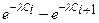 .
.
Проверим гипотезу 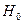 с помощью критерия согласия Хи-квадрат Пирсона .
с помощью критерия согласия Хи-квадрат Пирсона .
Вычислим параметр 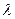 =
= 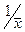 =
= 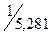 = 0,189358 = 0,189.
= 0,189358 = 0,189.
Так как изучается непрерывная случайная величина, то при вычислении значений 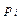 необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о показательном законе распределения.
необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о показательном законе распределения.
| Вид закона распределения | Первый интервал разбиения | Последний интервал разбиения |
| Экспоненциальный | 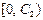 | 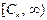 |
Вычислим вероятности по формуле 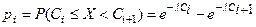
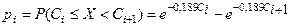 .
.
Пример расчета:
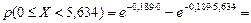 1- 0,344788 = 0,655212 = 0,655.
1- 0,344788 = 0,655212 = 0,655.
Для того, чтобы облегчить расчеты, можно с помощью пакета программ 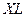 выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:
выполнить промежуточные расчеты, которые необходимо оформить в виде таблицы:
Таблица 1 - Расчетная таблица вероятностей
Граница интервала 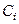 | 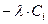 | 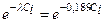 | 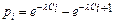 | 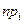 |
| 0,655212 | 0,655212 | |||
| 5,634 | -1,06483 | 0,344788 | 0,221096 | 0,221096 |
| 11,058 | -2,08996 | 0,123692 | 0,079318 | 0,079318 |
| 16,482 | -3,1151 | 0,044374 | 0,028455 | 0,028455 |
| 21,906 | -4,14023 | 0,015919 | 0,010208 | 0,010208 |
| 27,33 | -5,16537 | 0,005711 | 0,003662 | 0,003662 |
| 32,754 | -6,19051 | 0,002049 | 0,002049 | 0,002049 |
 | -  | - | - | |
| Итого | - | - |
Таблица 2 – Расчет c2
Границы интервалов 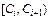 | Частоты эмпирические 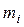 | Вероятности 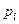 | Частоты теоретические 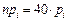 | 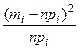 |
| [0; 5,634) | 0,655 | 26,21 | 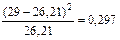 | |
| [5,634; 11,058) | 0,221 | 8,844 | 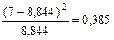 | |
| [11,058; 16,482) | 0,079 | 3,173 | 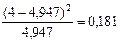 | |
| [16,482; 21,906) | 0,028 | 1,138 | ||
| [21,906; 27,33) | 0,01 | 0,408 | ||
| [27,33; 32,754) | 0,004 | 0,146 | ||
[32,754; 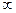 ) ) | 0,002 | 0,082 | ||
| Итого | 0,863 = c2 |
Вычислим число степеней свободы n = k – r – 1 = 3-1-1= 1 , где k = 3– число интервалов в таблице 2 после объединения, r =1 - число параметров выбранного закона распределения – в нашем случае показательный закон (один параметр 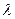 ).
).
По таблицам квантилей распределения c2 определяется критическое значение 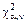 =
= 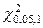 = 3,841 , соответствующее заданному уровню значимости a=0,05 и числу степеней свободы n = 1.
= 3,841 , соответствующее заданному уровню значимости a=0,05 и числу степеней свободы n = 1.
Вывод. Сравниваем полученное значение в таблице 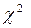 = 0,863 с табличным
= 0,863 с табличным 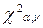 = 3,841. Так как расчетное
= 3,841. Так как расчетное 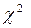 = 0,863 меньше, чем табличное
= 0,863 меньше, чем табличное 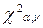 = 3,841, то гипотеза о показательном законе распределения подтвердилась.
= 3,841, то гипотеза о показательном законе распределения подтвердилась.
Пример.2.2
При проведении экспериментов фиксировались значения случайной величины X, характеризующей цены на зимнюю обувь (в у.е.).
Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х, построить гистограмму частот. По гистограмме частот выдвинуть нулевую гипотезу о виде закона распределения случайной величины 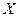 и проверить ее с помощью критерия согласия Пирсона.
и проверить ее с помощью критерия согласия Пирсона.
1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.
Таблица 1- Расчетная таблица
| Номер п/п | Выборка, у.е. | Вариационный ряд, у.е., 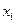 | 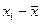 | 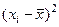 |
| -42,16 | 1777,466 | |||
| -38,16 | 1456,186 | |||
| -38,16 | 1456,186 | |||
| -30,16 | 909,6256 | |||
| -27,16 | 737,6656 | |||
| -25,16 | 633,0256 | |||
| -23,16 | 536,3856 | |||
| -23,16 | 536,3856 | |||
| -22,16 | 491,0656 | |||
| -22,16 | 491,0656 | |||
| -21,16 | 447,7456 | |||
| -18,16 | 329,7856 | |||
| -14,16 | 200,5056 | |||
| -13,16 | 173,1856 | |||
| -11,16 | 124,5456 | |||
| -9,16 | 83,9056 | |||
| -9,16 | 83,9056 | |||
| -8,16 | 66,5856 | |||
| -7,16 | 51,2656 | |||
| -6,16 | 37,9456 | |||
| -6,16 | 37,9456 | |||
| -4,16 | 17,3056 | |||
| -4,16 | 17,3056 | |||
| -1,16 | 1,3456 | |||
| 0,84 | 0,7056 | |||
| 0,84 | 0,7056 | |||
| 0,84 | 0,7056 | |||
| 4,84 | 23,4256 | |||
| 6,84 | 46,7856 | |||
| 6,84 | 46,7856 | |||
| 6,84 | 46,7856 | |||
| 6,84 | 46,7856 | |||
| 8,84 | 78,1456 | |||
| 9,84 | 96,8256 | |||
| 11,84 | 140,1856 | |||
| 12,84 | 164,8656 | |||
| 12,84 | 164,8656 | |||
| 13,84 | 191,5456 | |||
| 13,84 | 191,5456 | |||
| 15,84 | 250,9056 | |||
| 18,84 | 354,9456 | |||
| 22,84 | 521,6656 | |||
| 23,84 | 568,3456 | |||
| 24,84 | 617,0256 | |||
| 25,84 | 667,7056 | |||
| 26,84 | 720,3856 | |||
| 27,84 | 775,0656 | |||
| 30,84 | 951,1056 | |||
| 32,84 | 1078,466 | |||
| 55,84 | 3118,106 | |||
| Итого | 21562,72 |
2) Вычислим числовые характеристики.
Выборочное среднее: 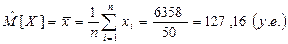 .
.
Мода: .
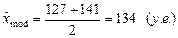 .
.
Медиана: 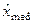 =
= 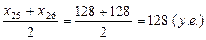 .
.
В качестве оценки дисперсии используется статистика
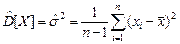 =
= 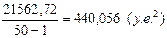 .
.
Оценка среднего квадратического отклонения
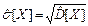 =
= 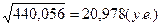 .
.
Оценка коэффициента вариации
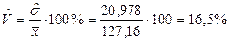 .
.
Найдем размах выборки 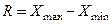 = 183-85 = 98.
= 183-85 = 98.
3) Вычислим длину интервала 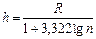 =
= 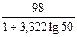 = 14.
= 14.
4) Границы интервалов:
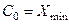 = 85,
= 85, 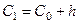 = 85+14 = 99,
= 85+14 = 99,
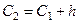 = 99+14 = 113,
= 99+14 = 113, 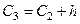 = 113+14 = 127,
= 113+14 = 127,
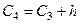 = 127+14= 141,
= 127+14= 141, 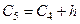 = 141+14 = 155,
= 141+14 = 155, 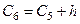 = 155+ 14 = 169,
= 155+ 14 = 169, 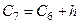 = 169 +14 = 183 =
= 169 +14 = 183 = 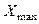 .
.
Построим гистограмму частот.
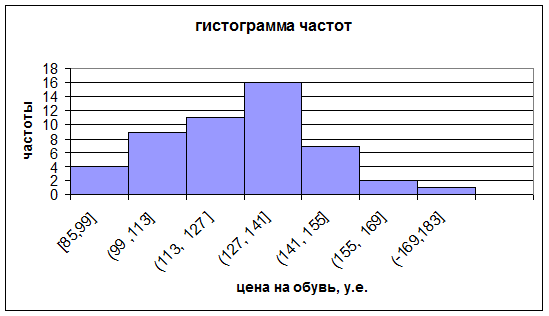
Рисунок 1 – Гистограмма частот
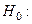 Случайная величина
Случайная величина 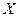 (цены на товары (в у.е.)) распределена по нормальному закону.
(цены на товары (в у.е.)) распределена по нормальному закону.
Выбираем уровень значимости 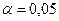 .
.
Так как изучается непрерывная случайная величина, то при вычислении значений 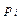 необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о нормальном законе распределения.
необходимо изменить границы первого и последнего частичных интервалов разбиения. В нашем случае проверяется гипотеза о нормальном законе распределения.
| Вид закона распределения | Первый интервал разбиения | Последний интервал разбиения |
| Нормальный | 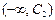 | 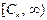 |
Вычислим вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения по формуле: 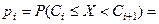
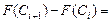
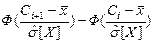 .
.
Проверим гипотезу с помощью критерия согласия Хи-квадрат Пирсона .
Вычислим параметр 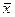 = 127,16,
= 127,16, 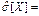 20,978.
20,978.
Вычислим вероятности по формуле 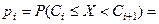
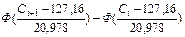
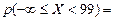
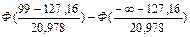 = =
= = 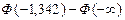 = -0,4099+0,5 = 0,0901,
= -0,4099+0,5 = 0,0901,
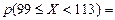
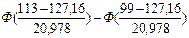 = =
= =  = - 0,2517 + 0,4099 = 0,1582,
= - 0,2517 + 0,4099 = 0,1582,
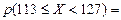
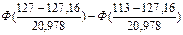 = =
= = 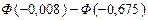 = - 0,0040 + 0,2517= 0,2477,
= - 0,0040 + 0,2517= 0,2477,
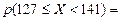
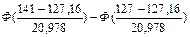 = =
= = 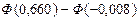 = 0,2454 + 0,0040 = 0,2494,
= 0,2454 + 0,0040 = 0,2494,
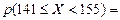
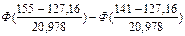 = =
= = 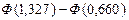 = 0,4082- 0,2454 = 0,1628,
= 0,4082- 0,2454 = 0,1628,
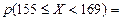
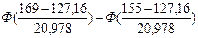 = =
= = 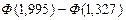 = 0,4772- 0,4082 = 0,069,
= 0,4772- 0,4082 = 0,069,
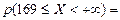
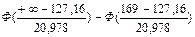 = =
= = 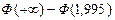 = 0,5 - 0,4772 = 0,0228.
= 0,5 - 0,4772 = 0,0228.
Таблица 2 – Расчет Хи-квадрат
Границы интервалов 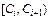 | Частоты эмпирические 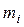 | Вероятности 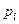 | Частоты теоретические 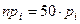 | 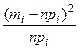 |
( 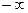 , 99] , 99] | 0,0901 | 4,505 | 0,028 | |
| (99 , 113] | 0,1582 | 7,91 | ||
| (113,127 ] | 0,2477 | 12,385 | 0,155 | |
| (127, 141] | 0,2494 | 12,47 | 0,999 | |
| (141, 155] | 0,1628 | 12,73 | 0,586 | |
| (155, 169] | 0,069 | |||
(169, 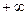 ) ) | 0,0228 | |||
| итого | 1,768= 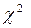 |
Вывод. По таблицам квантилей распределения c2 определяется критическое значение 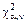 =
= 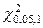 = 3,841 , соответствующее заданному уровню значимости a=0,05 и числу степеней свободы
= 3,841 , соответствующее заданному уровню значимости a=0,05 и числу степеней свободы 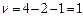 .Сравниваем полученное значение
.Сравниваем полученное значение 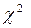 = 1,768 с табличным значением
= 1,768 с табличным значением 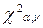 = 3,841. Так как расчетное
= 3,841. Так как расчетное 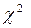 = 1,768 меньше, чем табличное
= 1,768 меньше, чем табличное 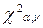 = 3,841, то гипотеза о нормальном законе распределения подтвердилась .
= 3,841, то гипотеза о нормальном законе распределения подтвердилась .
Лабораторная работа № 3
