Системы линейных уравнений общего вида

Система вида ---(9) называется системой общего вида.

Определение 31:Две системы называются равносильными (эквивалентными), если каждое решение первой системы являются решением второй и наоборот.

В системе (1) матрицу А= назовем основной матрицей системы, а = расширенной матрицей системы

Теорема. Кронекера-Капелли

Для совместности системы (9) необходим и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы, т. е. r(A)=r( )

Теорема 1. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема 2.Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Правило решения произвольной системы линейных уравнений:

1)найти ранги основной и расширенной матриц системы. Если , то система не совместна.

2) Если =r, то система совместна. Найти какой-либо базисный минор порядка r. Базисным будем называть минор, на основании которого определялся ранг матрицы.

Неизвестные, коэффициенты которых входят в базисный минор, называют главными (базисными) и оставляют слева, а остальные неизвестные называют свободными и переносят в правую часть уравнения.

3)Найти выражения главных неизвестных через свободные. Получено общее решение системы.

Пример 20: Исследовать систему и в случае ее совместности найти или единственное или общее решение

Решение: 1) по Т. Кронекера-Капелли находим ранги расширенной и основной матриц системы:

~ ~

~ ~ ранг основной матрицы равен двум

2) находим ранг расширенной матрицы ~ ~ ~

3) Вывод: =2, то система совместна.

Но 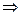система неопределенная и имеет бесчисленное множество решений.

4) Базисные неизвестные 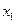и 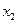, т. к. они принадлежат базисному минору, а - свободная неизвестная.

Пусть =с, где с – любое число.

5)Последней матрице соответствует система

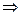
6)Ответ:

7) Проверка: в любое из уравнений исходной системы, где присутствуют все неизвестные, подставляем найденные значения.