Основные теоремы о дифференциалах

1 теорема. Дифференциал алгебраической суммы ф-ции = алгебраической суммы дифференциалов этих
ф-ций: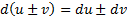

Док-во: 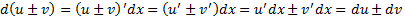ч.т.д.

2 теорема.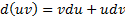

3 теорема.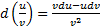

Дифференциал сложной ф-ции: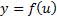

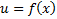
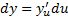
Таблица дифференциалов.

Правила:

1) алгебраической суммы: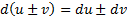

2)

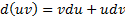
3)

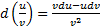
4) Дифференциал ф-ции: Это когда , ,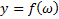

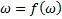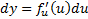
5)

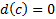
6)

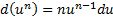
7)

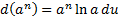
8)

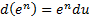
9)

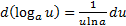
10)

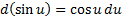
11)

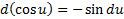
12)

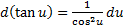
Применение дифференциалов к приближенным вычислениям

Производная функции y=f(x) это предел отношения преращения функции к приращению аргумента lim :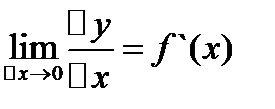

Воспользуемся теоремой: если lim z=A z=A+£ £à0

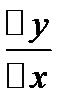=fʹ(x)+£ из этого равенства найдем 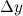следовательно 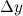=fʹ(x)▲x + 2 ▲x £à0

Отбросим бесконечно малые величины более высокого порядка, чем ▲x и получим ▲y

▲y=fʹ(x) ▲xà▲y=dy оно позволяет вычеслить с большей точностью приблежения приращение дифференцируемой функции

Дифференциалы высших порядков

Dy=fʹ(x)dx y=f(x) первый дифференциал функции есть также функции от x,можно найти ее дифференциал. Дифференциал от дефференциала функции y=f(x) называется вторым дифференциалом или дефференциалом второго порядка и обозначается d²y или d²f(x)

d²y=fʹʹ(x)dx ² d ³y=fʹʹʹ(x)dx ³ d ⁿ y=f⁽ⁿ⁾(x)dxⁿ

Правило лопиталя

Рассмотрим способы раскрытия неопределенносте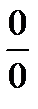й и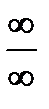

Предел отношения двуг бесконечно малых и бесконечно больших велечин равен пределу отношения их производных,если он существует или равен бесконечности. 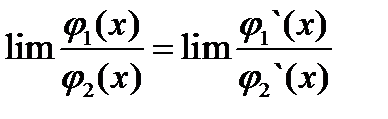Если этот предел равен бесконечности или существует,то он равен исследуемому пределу. Если отношение представляет coотношение двух бесконечно малых или двух бесконечно больших величин,то нужно применить правило Лопиталя

Формула Тейлора

Функции f(x)диффер n+1 раз в некотором интервале, содержащим точку x₀ может быть представлена в виде суммы многочлена n-степени и остаточного числа R_n

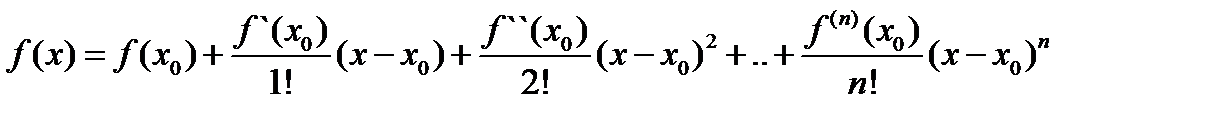
Где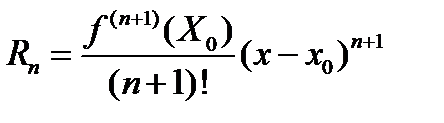

Разложение Функции f(x) по значению x-x₀ .Это позволяет приближенно представить произвольную функцию f(x) в виде многочлена

Частный вид формулы Тейлора

При 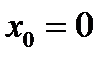,назыв формула Маклорена

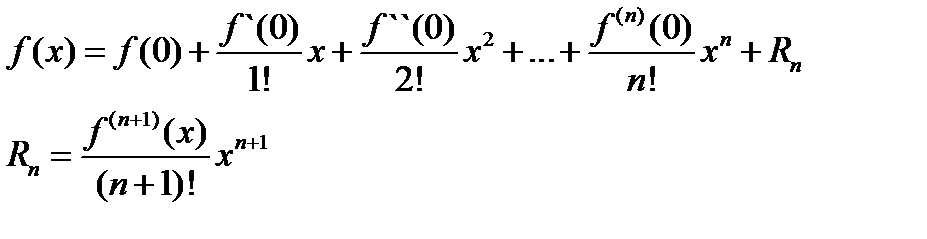
Она дает разложение ф-ции по степеням самой независимой переменной Х.Для некоторых ф-ций эта формула непременима,т.к при х=0,их ф-ции и производные не сущ.

Возростание и убывание функции

При изучении поведения функции получается ,что во всей области ее определение множество возрастает. При этом некоторые функции изменяются монотонно ,но только возрастают или только убывают. Многие функции изменяются не монотонно ,что в одних интервалах они возрастают а в другом убывают. Y=f(x)

Если в некотором интервале yʹ>0 ,то функция возрастает, если yʹ<0 ,то функция убывает на этом интервале

Вопрос 31.

Максимум и минимум ф-ции

Значение ф-ции y=f(X) в точке Хо наз max (min), если оно является наибольшим(наименьшим) по сравнению с её значениями в окресностях этой точки.

Ф-ция может иметь эустремумы max или min только в точке,лежащей в области определения ф-ции или не иметь их совсем,то в точке экстремума прозводная равна 0 или не сущ-ет.

Также точки называются критическими.Ф-ция имеет экстремум в тех точках экстремума,в которых производная меняет знак и сама ф-ция непрерывна.Чтобы найти эти точки нужно:

1)Найти у ' и критические точки в которых у '=0 или не сущ-ет и которые лежат внутри ООФ.

2)а)Определить знак у ' слева и справа от каждой из критических очек,если при переходе аргумента Х через критич. точку Хо у ' меняет знак с + на - ,то Хо-точка max,если с — на +,то Хо- точка min. Если у ' не меняет знак,то в точке Хо-экстремума нет. Иногда исследуют критич.точку по знаку у ''

б) находим у '' и определяем ее знак в каждой критич.точке:

-если у ''>0,то Хо-min

-если у ''<0,то Хо-max

-если у ''=0,то Хо-вопрос о наим.экстремуме в т. Хо остаётся открытым,её можно исследовать по правилу (а)

Далее следует найти экстремум ф-ции,т.е. вычислить значение ф-ции,найденное в точках экстремума.

Вопрос 32.