Определение опорных реакций балок
На опорах балок возникают реакции, с определения которых следует начинать решения всех задач по расчету изгиба.
Реакции опор определяются из уравнений равновесия (статики), которые можно представить в двух различных вариантах:
1) в виде суммы проекций всех сил на оси х и у, а также суммы моментов сил (включая реакции) относительно любой точки по оси балки:
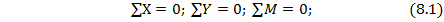
2) в виде суммы всех сил на одну из координатных осей х или у и двух сумм моментов сил (включая реакции) относительно двух точек, лежащих на оси балки:
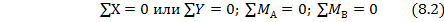
Выбор того или оного варианта составления уравнений равновесия, а также выбор точек по направлению координатных осей, используемых при составлении этих уравнений, производится в каждом конкретном случае с таким расчетом, чтобы по возможности не производить совместное решение уравнений. Для проверки правильности определения опорных реакций полученные их величины рекомендуется подставлять в какое-либо уравнение равновесия, не использованное ранее.
При определении реакций их направления можно выбирать произвольно. Если же реакции в расчете оказались отрицательными, то это означает, что их направление выбрано неправильно. В этом случае на расчетной схеме первоначальное направление реакций перечеркивают и указывают их обратное направление. В последующих расчетах величины реакций считаются положительными.
Однако можно заранее предугадать правильное направление реакций на основании мысленно представленной упругой линии балки после ее нагружения внешними усилиями (рис 8.5): при «отрыве» балки от опоры (опора А) реакция RА имеет направление к опоре; при «вдавливании» балки в опору (опора В) реакция RВ имеет направление от опоры.
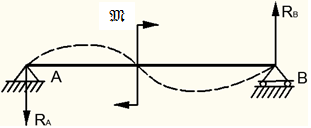
Рисунок 8.5 – К определению направлению реакций
Рассмотрим типичные случаи определения реакций для простейших видов нагрузок.
Если на балку действует распределенная нагрузка интенсивностью q, как показано на рис.8.6, то при определении опорных реакций нагрузка заменяется ее равнодействующей Р, равной произведению интенсивности нагрузки q на длину участка ее действия l
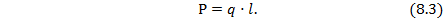
Примером сплошной равномерно распределенной нагрузки может служить собственный вес балки или часто расположенные нагрузки на участке ее длины.
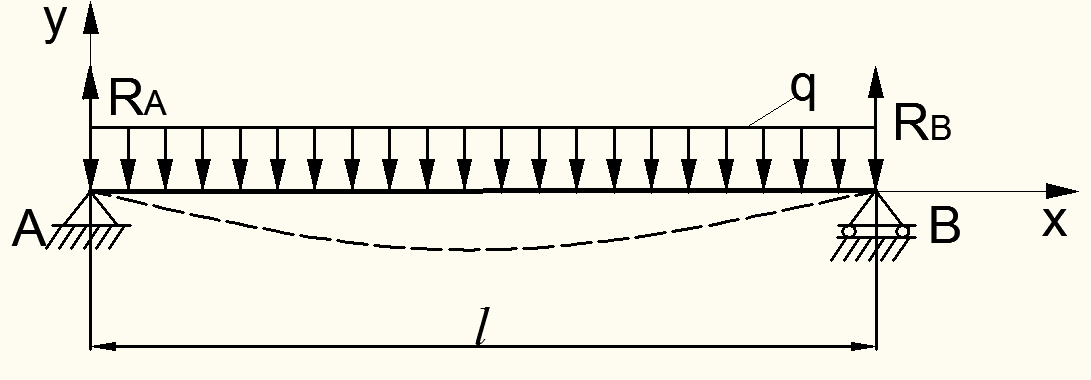
Рисунок 8.6 – Случай равномерно распределенной нагрузки на балку
Точка приложения сплошной равномерно распределенной нагрузки q лежит посредине того участка, на который она действует; при треугольном законе действия распределенной нагрузки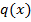 
равнодействующая прикладывается по ее центру тяжести.
Размерность интенсивности нагрузки q выражается обычно в кН/м или кН/см.
Рассмотрим последовательность определения опорных реакций для случая нагрузки балки, показанной на рис.8.7:
1. На расчетной схеме балки показывается принятое направление реакций RА и RВ , возникающих на опорах. Поскольку внешняя нагрузка действует в вертикальной плоскости перпендикулярно оси балки, то горизонтальная реакция на шарнирно-неподвижной опоре А отсутствует.
2. Поскольку в данном случае неизвестных реакций две (RА и RВ), то в качестве равновесия для определения реакций принимается два уравнения
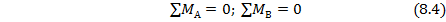
При составлении этих условий равновесия следует принять правило знаков для моментов сил, включая реакции. Обычно принимается такое привило для внешних (активных) знаков: если моменты от сил направлены по часовой стрелке, то они считаются положительными.
Тогда первое условие равновесия (8.4) приводит к уравнению относительно неизвестной реакции RВ (см. рис.8.6)
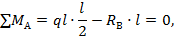
откуда
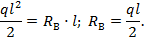
Реакция получалась положительной, следовательно ее направление принято правильным.
Аналогично используем второе условие равновесия (8.4), приводящее к уравнению относительно второй реакции RА:
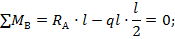
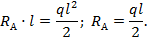
Снова реакция оказалась положительной, следовательно ее первоначально направление на расчетной схеме выбрано правильно.
3. Правильность определения величин реакций проверяем из использования еще одного, ранее не использованного, условия равновесия
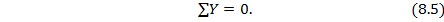
При этом проекции сил, совпадающих с направлением оси у, считаются положительными, а направленных в обратную сторону – отрицательными.
Тогда на основании использования условия (8.5) имеем:
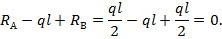
Полученное тождество (0=0) свидетельствует о правильности определения величин реакций в расчете изгиба балки.
Рассмотрим другой типичный случай нагрузки в виде внецентренно расположенной сосредоточенной силы Р по длине балки l (рис.8.7).
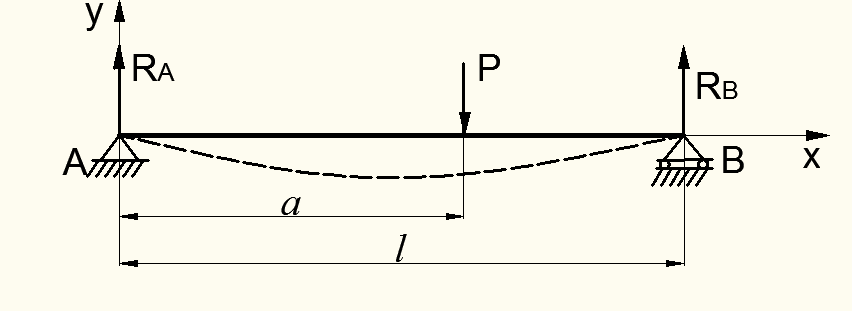
Рисунок 8.7 – Случай нагрузки балки сосредоточенной силой
1. Покажем на расчетной схеме реакции RА и RВ. Они направлены, как было указано выше, навстречу нагрузке.
2. Реакции определим из условий равновесия:
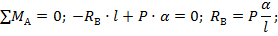
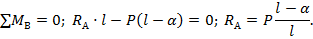
Реакции получились положительными, следовательно, их первоначальное направление на расчетной схеме выбрано верно.
Заметим заодно, что реакция на опоре В оказалась больше, чем реакция на опоре А: RВ˃RА . Это следует из того, что сила Р находится ближе к опоре В, а значит и нагружает ее больше.
3. Проверка:
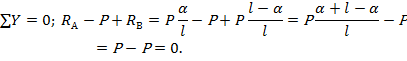
Полученное тождество свидетельствует о правильности определения реакции.
Рассмотрим еще один случай нагрузки балки в пролете внешним сосредоточенным моментом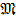 
(рис. 8.8), что имеет место в практических расчетах изгиба.
| 𝔐 |
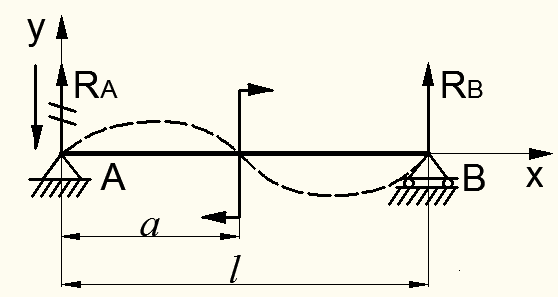
Рисунок 8.8 – Случай нагружения балки сосредоточенным моментом
1. Покажем на расчетной схеме предполагаемое направление реакций (вначале мы не знаем, правильно ли приняты такие направления).
2. Реакции определяем из уравнений равновесия:
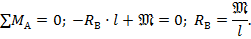
Реакция получилась положительной, следовательно, ее первоначальное положение выбрано верно.
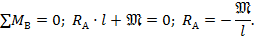
Реакция оказалась отрицательной, а это означает, что ее направление выбрано неправильно. Поэтому на расчетной схеме зачеркиваем первоначально (ошибочно) принятое направление RА и показываем обратное (истинное) направление (см.ри.8.8). В дальнейших расчетах считаем реакцию RА с правильным направлением положительной.
3. Проверка:
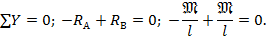
Использованное уравнение равновесия для балки выполняется, а это означает правильность определения реакций и их направления.
Если балка при поперечном изгибе имеет такие опоры, что общее число реакций, возникающих на опорах, не превышают двух, то реакции всегда могут быть определены из двух уравнений равновесия типа (8.2). Такие балки, реакции которых определяются из этих уравнений статики, называются статически определимыми балками. Эти балки могут быть таких простейших видов (рис. 8.9):
Рисунок 8.9 – Статически определимые балки
1) балка с одним жестко защемленным и другим свободным концом, иначе консоль (рис.8.9, а); 2) шарнирно-опертые балки (рис.8.9, б и 8.9, в).
Балки, у которых общее число реакций опор больше числа уравнений равновесия, называются статически неопределимыми (расчет их изгиба будет рассмотрен в п. 8.10). Для таких балок реакции опор определяются из совместного решения уравнений статики и условий совместимости деформаций.