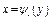Свойства двойного интеграла

Лекция № 1 ДВОЙНОЙ И ТРОЙНОЙ ИНТЕГРАЛЫ

Двойной интеграл и его свойства

Пусть функция 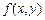определена в некоторой замкнутой области 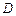плоскости 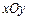. Разобьем область 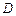произвольным образом на 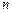частей 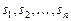с площадями 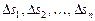. Внутри каждой элементарной области 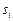выберем произвольную точку 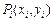и найдем значение функции 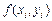в этой точке. Составим сумму:

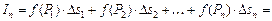
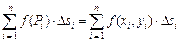
Эта сумма называется 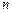-й интегральной суммой для функции 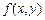по области .

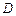Диаметром области 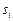назовем наибольшее из расстояний между точками границы этой области и обозначим .

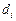Опр.Если существует конечный предел последовательности интегральных сумм 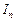при стремлении к нулю наибольшего из диаметров частичных областей 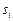, не зависящий ни от способа разбиения области 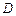, ни от выбора точек 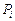, то он называется двойным интегралом от функции 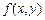по области 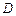и обозначается 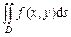. Таким образом,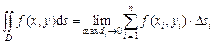

Свойства двойного интеграла

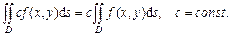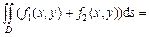
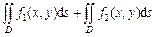1. ; 2. . 3. Если область 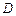разбить на две област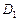и и 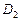без общих внутренних точек, то .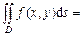

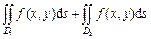§ 2. Вычисление двойного интеграла в прямоугольных декартовых координатах

В ДПСК элемент площади 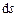можно записать в виде произведения 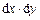. Тогда = .

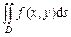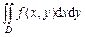Область 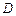называется правильной в направлении ос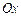и (или 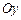), если любая прямая, проходящая параллельно этой оси, пересекает границу области 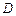не более, чем в двух точках. Например, область 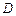на рис. является правильной в направлении оси 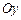и неправильной в направлении оси 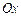(прямая 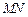пересекает границу области 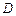в четырех точках).

Вычисление двойного интеграла сводится к вычислению повторного интеграла.

1)Пусть область 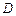является правильной в направлении оси и ограничена линиями: 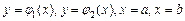, причем , .

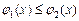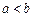При выборе внешнего интегрирования по переменной x для определения внутренних пределов интегрирования по переменной y по области интегрирования проводим прямую, параллельную оси 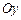снизу вверх. Прямая сначала пресекает кривую 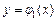, которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую 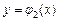, которую назовем линией выхода. То есть значение переменной 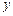в области 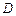меняется в пределах 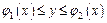.Тогда 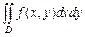= 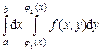. Правая часть формулы называется повторным интегралом. Таким образом, вычисление двойного интеграла свелось к вычислению повторного (двух определенных интегралов) интеграла вида 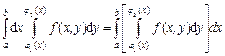. При вычислении «внутреннего интеграла» x считается постоянным.

2) 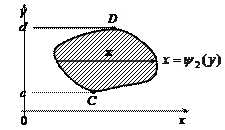Пусть область 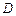является правильной в направлении оси 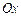и ограничена линиями: 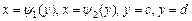, причем , .

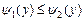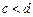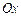При выборе внешнего интегрирования по переменной y для определения внутренних пределов интегрирования по переменной x по области интегрирования проводим прямую, параллельную оси слева направо. Прямая сначала пресекает кривую 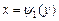, которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую 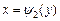, которую назовем линией выхода. То есть значение переменной 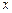в области 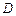меняется в пределах .

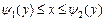Тогда 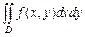= 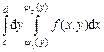. При вычислении «внутреннего интеграла» y считается постоянным.

Следовательно, 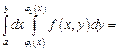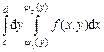. Переход от левой части равенства к правой и наоборот называется изменением порядка интегрирования. Если область интегрирования является неправильной, то ее можно представить как объединение правильных областей. Тогда двойной интеграл равен сумме двойных интегралов по этим областям.