С астатизмом второго порядка

Пример 4.1. Синтезировать регулятор положения с применением ЛЧХ на основе критерия динамической точности системы. Для расчетов принять следующие параметры:

– максимальная угловая скорость нагрузки W_max = 50 град/с;

– максимальное угловое ускорение нагрузки e_max = 10 град/с²;

– ошибка по скорости Da_W = 20 мин;

– ошибка по ускорению Da_e = 35 мин.

Моментную составляющую ошибки определить при отработке квадратично возрастающего момента сопротивления .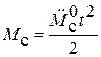

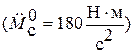Параметры двигателя, БП, ТГ и цифрового регулятора скорости принять из примеров 1.1, 2.1, 3.1.

Решение. 1. Определяем параметры желаемой передаточной функции ЭП (4.6). Коэффициент передачи по ускорению будет равен:

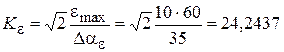с^{– 2}.

Значение базовой частоты определится по формуле (4.4) и будет равно:

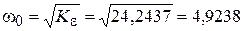с^{– 1}.

По выражениям (4.7) рассчитываем постоянные времени:

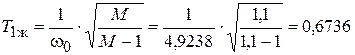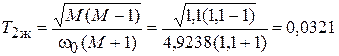с;

с.

С учетом проведенных расчетов запишем желаемую передаточную функцию ЭП с астатизмом второго порядка:

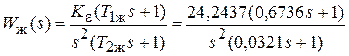. (4.13)

2. Для построения ССДМ неизменяемой части ЭП необходимы параметры тахогенератора и контура скорости:

– коэффициент передачи тахогенератора К_тг = 0,0318 В·с/рад;

– постоянная времени тахогенератора Т_тг = 0,0018 с;

– суммарная малая постоянная времени К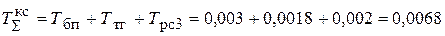С

с;

– коэффициент передачи датчика положения К_дп = 40 рад/В;

– передаточное число редуктора i = 358.

По перечисленным параметрам записываем передаточную функцию замкнутого контура скорости:

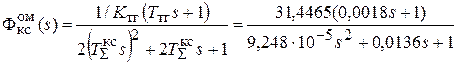. (4.14)

3. Составляем программу 1 в среде MatLab для определения передаточной функции регулятора положения ЭП с астатизмом второго порядка согласно формулам (4.12), (4.13) и (4.14).

Программа 1

>> num1=[К_εT_1ж К_ε];

>> den1=[T_2ж 1 0 0];

>> sys1=tf(num1, den1);

>> num2=[К_дпT_тг/К_тг К_дп/К_тг];

>> den2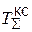=[2( )²i 2 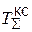i i 0];

>> sys2=tf(num2, den2);

>> sys=sys1/sys2

Transfer function:

0.5405 s^4 + 80.31 s^3 + 5964 s^2 + 8679 s

------------------------------------------

0.07268 s^4 + 42.64 s^3 + 1258 s^2

4. Составляем программу 2 в среде MatLab и определяем ЛАЧХ регулятора положения, изображенную на рис. 4.2.

Программа 2

>> w=logspace(-2, 4);

>> num=[0.5405 80.31 5964 8679 0];

>> den=[0.07268 42.64 1258 0 0];

>> bode(num, den, w)

Переходим к анализу полученного графика. Низкочастотный участок ЛАЧХ регулятора положения проходит под наклоном –20 дБ/дек, постепенно изменяя наклон к среднечастотному участку до 0 дБ/дек. Высокочастотный участок полученной ЛАЧХ (w ³ 100 с^{– 1}) с увеличением частоты изменяет свой наклон от 20 до 0 дБ/дек.

Таким образом, проведенный анализ показывает, что ЛАЧХ следует аппроксимировать четырьмя асимптотами (рис. 4.2) и придать регулятору положения свойства ПИД-регулятора.

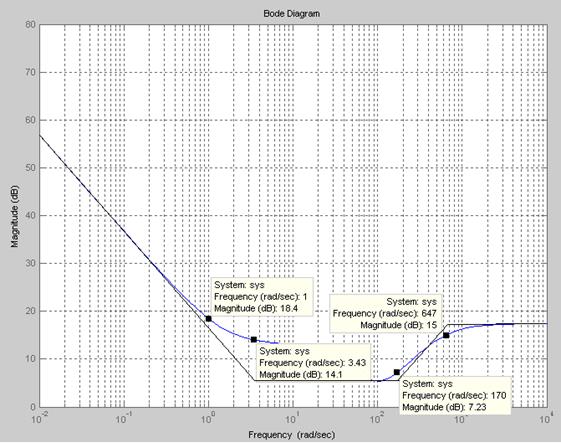
Рис. 4.2. ЛАЧХ регулятора положения

Рассчитаем параметры передаточной функции регулятора положения. На частоте w = 1 находим:

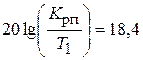дБ, (4.15)

откуда 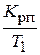= 8,3176 с^{– 1}.

По графику, представленному на рис. 4.2, определяем частоты сопряжения w₁ = 3,43 с^{– 1}; w₂ = 170 с^{– 1}; w₃ = 647 с^{– 1} и рассчитываем постоянные времени:

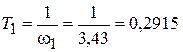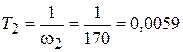с;

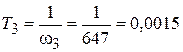с;

с.

Подставляя значение Т₁ в (4.15), получаем коэффициент передачи регулятора положения К_рп:

.

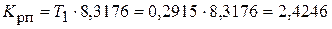С учетом полученных значений передаточная функция синтезированного регулятора положения принимает вид:

.

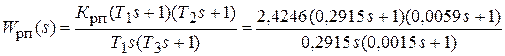Для построения динамической модели ЭП представим передаточную функцию РП (ПИД-регулятора) в виде:

.

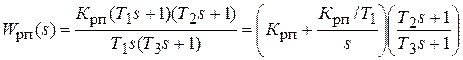Данная модель ПИД-регулятора четко показывает все три составляющие алгоритма его работы: пропорциональную К_рп, интегральную 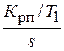и дифференциальную составляющую, представленную в виде форсирующего звена первого порядка ( 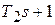). Заметим, что первая составляющая обеспечивает передачу сигнала, пропорциональную коэффициенту К_рп. Интегральная составляющая обеспечивает точность работы системы за счет сведения к нулю установившейся ошибки при отработке линейно возрастающего сигнала
a_з = W_maxt. Дифференциальная составляющая обеспечивает увеличение запасов устойчивости по фазе и амплитуде и требуемую колебательность процесса.

5. С учетом рассчитанных параметров получаем ССДМ ЭП (рис. 4.3) с аналоговым контуром положения и цифроаналоговым контуром скорости, который был синтезирован в примере 3.2.

Рис. 4.3 Структурная схема динамической модели электропривода в среде MatLab

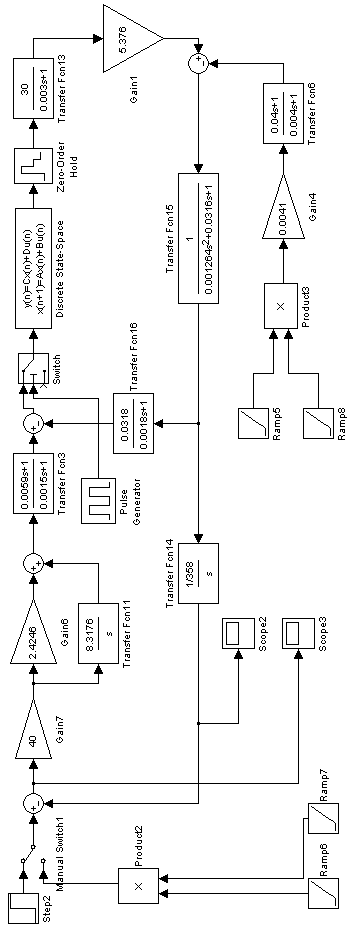
Особенностью схемы, показанной на рис. 4.3, является наличие блоков Ramp5, Ramp6, Ramp7, Ramp8, служащих для формирования квадратично возрастающих воздействи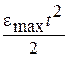й и 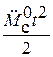на выходах умножителей Product2, Product3.

Блок Ramp (рис. 4.4), реализующий линейно возрастающий сигнал, находится в библиотеке блоков Sources.

В диалоговые окна блоков Ramp6 и Ramp7 (рис. 4.5) вводятся, соответственно, значения 1 и .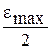

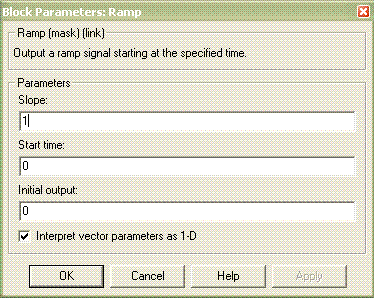Рис. 4.4. Блок Ramp	Рис. 4.5. Диалоговое окно блока Ramp

Аналогично, в диалоговые окна блоков Ramp5 и Ramp8 вводятся значения 1 и 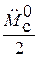, соответственно.

Результаты моделирования показаны на рис. 4.6 – 4.8.

Анализ графика (рис. 4.6) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 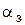примерно за 1,0 с
с перерегулированием 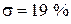и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1.

Поскольку контур положения содержит ПИД-регулятор положения, очевидно, что при ступенчатом и линейно возрастающем задающем воздействии статическая ошибка и ошибка по скорости будут равны нулю.

a(t), рад

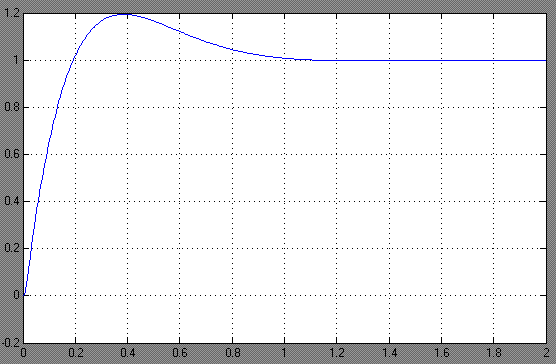t, c

Рис. 4.6. Переходная характеристика системы по задающему воздействию

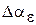, рад

t, c

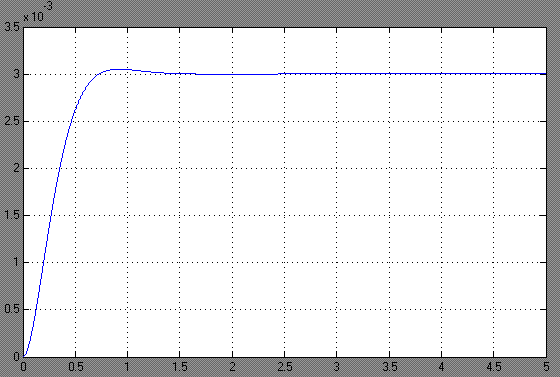
Рис. 4.7. График ошибки системы

при квадратично возрастающем задающем воздействии

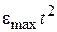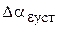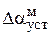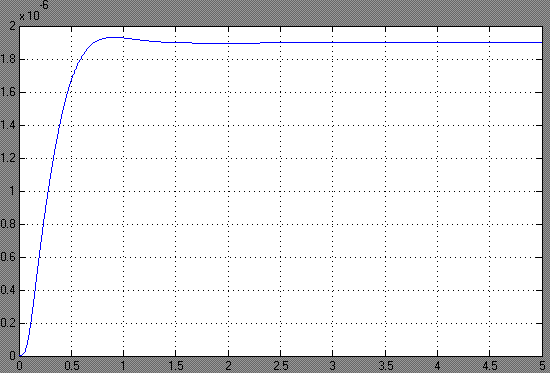
На рис. 4.7 представлена характеристика при отработке типового задающего воздействия /2. Установившаяся ошибка системы составляет 10,26 мин. Моментная составляющая ошибки при отработке квадратично возрастающего момента сопротивления 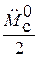составляет 0,0065 мин по истечении 2,5 с (рис. 4.8).

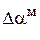, рад

t, c

Рис. 4.8. График моментной составляющей ошибки системы

при квадратично возрастающем моменте сопротивления