Взаимодействие параллельных токов. Основная электрическая единица СИ – Ампер.

Магнитное поле движущегося заряда. Магнитная сила. Сила Лоренца. Сила Ампера. Общая формулировка закона Ампера. Теорема о циркуляции индукции магнитного поля. Формула Стокса. Примеры применения теоремы о циркуляции индукции магнитного поля: бесконечный прямой проводник, соленоид, тороидальная катушка. Уравнения Максвела.

Магнитное поле движущейся

Заряженной частицы

Движущаяся заряженная частица эквивалентна элементу

тока и создаёт в окружающем пространстве магнитное поле.

В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под cвободным движением заряда понимается его движение с постоянной скоростью.

Этот закон выражается формулой:

где г — радиус-вектор, проведенный от

заряда Q к точке наблюдения М, v - скорость заряда.

Модуль магнитной индукции вычисляется по формуле:

где α — угол между векторами и .

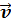Таково магнитное поле, порождаемое любой движущейся

заряженной частицей – электроном проводимости в металле или в пучке

электронно-лучевой трубки или в вакуумном диоде, иона в растворе

электролита, если скорость много меньше скорости света. Магнитное

поле создают и движущиеся заряженные тела макроскопических

размеров.

Закон Ампера

В 1820 г, как уже упоминалось ранее, Амперу удалось установить

экспериментальным путём закон для силы магнитного

взаимодействия двух длинных прямолинейных параллельных

проводников с постоянным током : F_А ~ I₁ ∙ I ₂ / r . Этот закон является частным случаем общего закона Ампера для элемента тока:

Элементарная сила d 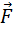, действующая на малый элемент длины d проводника с током, находящийся в магнитном поле индукцией , прямо пропорционален силе тока I в проводнике и векторному

произведению

Направление d с направлением тока в проводнике.

Направление вектора d может быть найдено, согласно общим правилам векторного произведения, по правилулевой руки:

если ладонь левой руки расположить

так, чтобы в нее входил вектор , а четыре вытянутых пальца — по направлению тока в проводнике, то отогнутый на 90⁰ большой палец покажет направление силы, действующей на ток.

В некоторых случаях удобнее использовать правило левой руки в более детальной формулировке:

Если ладонь левой руки расположить таким образом,

что В_┴ входит в ладонь, а четыре выпрямленных пальца направлены по току, то большой палец, отогнутый на 90⁰, указывает направление F_A.

Модуль силы Ампера вычисляется по формуле:

где α — угол между векторами d и

Интегрирование этого выражения по известной длине проводника даст знакомую всем интегральную формулу для вычисления модуля силы Ампера, действующей на проводник с током во внешнем магнитном поле : F= IBLsinα.

Взаимодействие параллельных токов. Основная электрическая единица СИ – Ампер.

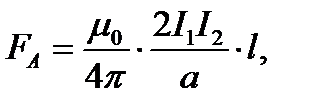Подставляя в последнюю формулу выражение для магнитной индукции В₁ бесконечного проводника c током I₁ получим:

Где а – расстояние между проводниками, l – длина проводников, μ₀ –

магнитная постоянная μ₀=4π∙10^-7Гн/м.

При одинаковых токах в проводниках

В системе СИ сила магнитного взаимодействия проводников используется для определенияосновной электрической единицы СИ – Ампер.

1 Ампер (А) – это сила такого постоянного тока, при прохождении которого по двум прямолинейным бесконечно длинным проводникам, находящихся в вакууме на расстоянии 1 метр друг от друга, сила их взаимодействия составляет 2·10^-7 Н на каждый метр длины.

Закон Ампера

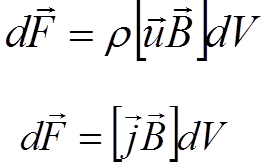
ρ = n - плотность носителей тока, dV – объём проводника, u - скорость упорядоченного движения, j =

Сила Лоренца

Магнитное поле действует не только на токи, но и на движущиеся заряженные частицы. Такая сила получила название силы Лоренца.

Эта сила равна:

Её модуль:

С формальной точки зрения можно сказать, что движущаяся

заряженная частица представляет собой “элемент тока”, поэтому

выражение для силы Лоренца нетрудно «вычислить» как

«удельную силу Ампера». Для этого достаточно всего лишь

рассмотреть малый элемент проводника с током в магнитном

поле и разделить «интегральную магнитную силу» – силу Ампера

– на число упорядоченно движущихся заряженных частиц.

Закон Ампера: на элемент dl проводника с током I действует сила

На одну заряженную частицу в элементе тока Idl действует сила Лоренца:

где dN – число частиц в объеме проводника длиной dl.

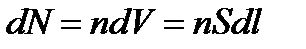
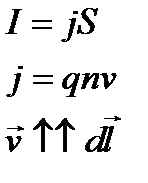
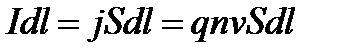
Однако этот вывод не является «доказательством» закона

– этот закон должен быть установлен экспериментально!

Направление силы Лоренца определяется с помощью правила левой руки:

если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q > 0 направления I и v совпадают, для Q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд.

Сила Лоренца всегда перпендикулярна скорости движения заряженнойчастицы, поэтому она изменяет только направление этой скорости, не меняя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Анализ формулы показывает, что если частица

влетает параллельно вектору ,то F_л= 0 и траектория частицы прямая линия.

Если заряженная частица движется в магнитном поле со скоростью , перпендикулярной вектору (α = 90⁰),то сила Лоренца постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус которой определяется из условия:

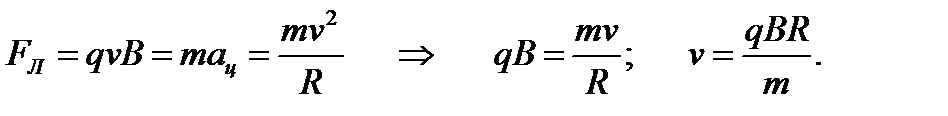
Если заряженная частица влетает в магнитное поле под некоторым углом (0⁰ < α < 90⁰), то она будет двигаться по цилиндрической спирали.

Шаг спирали: