Трение скольжения. Законы Кулона. Угол и конус трения

Между движущимися телами в плоскости их соприкосновения возникает сила трения скольжения. Обусловлено это прежде всего шероховатостью соприкасающихся поверхностей и наличием сцепления у прижатых тел.

В инженерных расчетах обычно пользуются установленными опытным путем закономерностями, которые с некоторой степенью точности отражают действие силы трения. Эти закономерности называют законами трения скольжения (Кулона). Их можно сформулировать следующим образом.

1. При стремлении сдвинуть одно тело относительно другого в плоскости их соприкосновения возникает сила трения F , модуль которой может принимать любые значения от нуля до Fmax, т. е. . Сила трения приложена к телу и направлена в сторону, противоположную возможному направлению скорости точки приложения силы.

2. Максимальная сила трения равна произведению коэффициента трения f на силу нормального давления N: .

Коэффициент трения f — безразмерная величина, зависящая от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.). Определяют его опытным путем.

Различают коэффициенты трения покоя и трения скольжения, причем последний, как правило, зависит и от скорости скольжения. Коэффициент трения покоя соответствует такой
максимальной силе трения Fmax, при которой имеется предельное состояние равновесия. Малейшее увеличение внешних сил может вызвать движение. Коэффициент трения покоя, как правило, немного больше коэффициента трения скольжения. С увеличением скорости скольжения значение коэффициента трения скольжения сначала незначительно уменьшается, а затем остается практически неизменным. Значения коэффициентов трения для некоторых пар трения следующие: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25; сталь по льду 0,027.

3. Максимальная сила трения в довольно широких пределах не зависит от площади соприкасающихся поверхностей.

Силу трения скольжения иногда называют силой сухого трения.

Реакция шероховатой поверхности. Угол трения.

Реакция идеально гладкой поверхности, как уже говорилось выше, направлена по нормали к поверхности. На шероховатой поверхности могут возникать силы трения скольжения. Поэтому реакцию шероховатой поверхности представим в виде двух составляющих: нормальной реакции N (равна по модулю силе нормального давления) и перпендикулярной ей силы трения F.

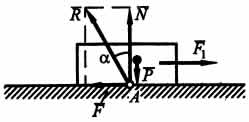
Полная реакция R=N + F всегда отклонена от нормали к поверхности на некоторый угол "альфа". На рисунке видно, что 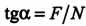. Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу F1, мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения F = -F1, причем . С увеличением силы F1 будет возрастать и сила F . Наконец, при F1 = Fmax наступит предельное состояние равновесия, при котором полная реакция R отклонится от вертикали на угол "альфа"max, называемыйуглом трения. Обозначив его через "фи", получим .

Тангенс угла трения равняется коэффициенту трения. Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения.

Конус трения.

Рассмотрим равновесие невесомого тела на горизонтальной шероховатой плоскости под действием наклонной силы F1, стремящейся его сдвинуть.

Тело будет сдвинуто только тогда, когда > Fmax = 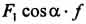. Предельному случаю равновесия соответствует такой угол
наклона a, при котором выполняется равенство = 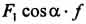, или tgα = f. Если tgα<=f, то как бы не возрастала сила F1, тело сдвинуть с места невозможно. Возрастающей сдвигающей силе будет противостоять пропорционально ей увеличивающаяся сила трения .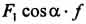

Поворачивая вокруг вертикали вектор силы F1 и сохраняя при этом предельное равновесие, опишем конус, называемый конусом трения. Если свойства соприкасающихся поверхностей во всех направлениях одинаковы, то угол а будет постоянным, а конус трения круговым. Конус трения обладает тем замечательным свойством, что если действующая на тело сила находится внутри него, то тело всегда будет находиться в равновесии. Этим объясняются известные явления заклинивания, или самоторможения тел.