График зависимости момента инерции от квадрата расстояний.

Федеральное государственное

Бюджетное образовательное учреждение

Высшего образования

Санкт-Петербургский

Горный университет

Кафедра общей и технической физики

Отчет

По лабораторной работе №6

Определение момента инерции с помощью маятника обербека

Выполнил студент: Илли М.В.

Проверил доцент: Фицак В.В.

Санкт-Петербург

Цель работы - исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины.

Краткое теоретическое содержание:

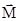В основе опыта лежит основное уравнение динамики вращательного движения твердого тела , где - суммарный момент внешних сил; J - момент инерции тела относительно той же оси; - угловое ускорение.

В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения. Из основного уравнения динамики вращательного движения твердого тела следует, что угловое ускорение e вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения.

Явление изученное в процессе работе:

Вращательным движением твердого теланазывается явление, когда при вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Основные определения физических величин, явлений, процессов:

Момент инерции телаявляется мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.

Моментом инерции материальной точки относительно некоторой оси называется величина J,равная произведению масс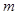материальной точки на квадраты её расстояния от оси. ,где m-масса материальной точки, r-расстояние от материальной точки до оси.

Момент инерции твердого тела (сплошного)называется величинаJ, равная произведениюмассытела- 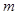на радиус- 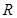относительно оси, проходящей через центры оснований.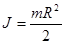

Моментом инерции системы материальной точки относительно осиназывается величина J,равная сумме произведений массвсех материальных точек, образующихмеханическуюсистему, на квадраты их расстояний 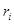от данной оси.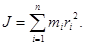

Закон и соотношения

-основное уравнение динамика вращательного движение твердого тела:

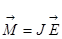
где: 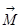--суммарный момент внешних сил; 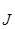—момент инерции тела относительно той же оси; 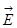—угловое ускорение

[M]=н*м

,

-Второй Закон Ньютона:

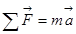; m=const. где a--ускорение тела, m—масса тела. F—сила натяжения

[M]=кг [F]=H [a]=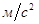

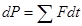
--изменение импульса тела

F—сила натяжения

[P]=Н*с

[F]=Н

Теоретические ожидания. Результат.

1. Расчётные формулы:

. где 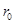– радиус шкива, m- масса груза, h – путь, пройденный грузом

, где 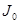– момент инерции крестовины без грузов.

2. Формулы погрешности:

.

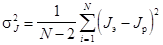Таблица 1(Расчет момента инерции тела).

№	r, м	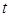, c	, c	Jэ кг*м2	Jр кг*м2
	0,25	8.633	8.6320	0.1236	0,120696
	8.638
	8.625
	0,22	7.836	7.7057	0,0985	0,9338
	7.700
	7.581
	0,19	6.144	6.1763	0,0632	0,069768
	6.010
	6.375
	0,16	5.066	5.0920	0.0429	0,049513
	5.084
	5.126
	0,13	4.068	4.0497	0,0271	0,03273
	4.048
	4,033
	0,10	3.541	3,4440	0,0195	0,01942
	3,405
	3,386
	0,07	2.859	2.8090	0,0129	0,009581
	2.770
	2.798

Таблица 2(Обработка результатов эксперимента)

№	r, м	xi	Ji		xiJi
	0,25	0.0625	0.1236	0.0039	0.007728
	0,22	0.0484	0.0985	0,0023	0.004768
	0,19	0.0361	0.0632	0,0013	0.002282
	0,16	0.0256	0.0429	0,00065	0.001099
	0,13	0.0169	0,0271	0,000286	0.000458
	0,10	0.01	0,0195	0.0001	0.000195
	0,07	0.0049	0,0129	0,000024	0.000063
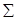		0.0292	0.0554	0,001231	0.0023709

Примеры расчётов:

m – масса груза, кг;

r₀ – радиус шкива, м;

g – ускорение свободного падения;

t – время движения груза;

h – путь, пройденный грузом

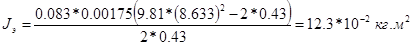
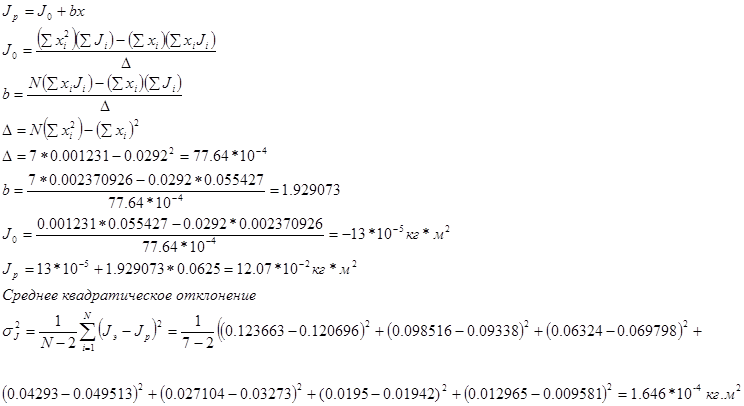
Окончательный результат:

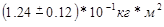
График зависимости момента инерции от квадрата расстояний.

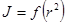
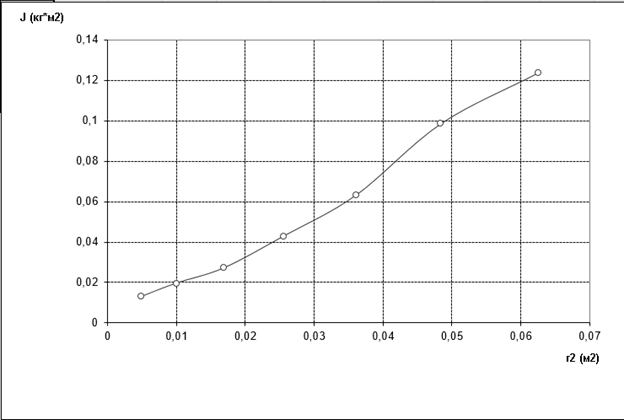
Вывод: После проведения опытов и произведения расчётов над полученными результатами, был определён момент инерции с помощью маятника Обербека. Результаты вычислений зафиксированы. И пришли к выводу, что при уменьшении радиуса вращения время вращения уменьшается Построив график прямопропорцианальная, чем больше радиус шкива, тем больше момент инерции системы зависимости момента инерции от квадрата радиуса шкива видим что зависимость