Розв’язання транспортної задачі методом потенціалів

Для визначення оптимального плану транспортної задачі розроблено декілька методів. Але найбільш часто використовуються метод потенціалів і метод диференціальних рент.

Загальний принцип визначення оптимального плану транспортної задачі методом потенціалів аналогічний принципу розв’язання задачі лінійного програмування симплексним методом, тобто: на початку знаходять опорний план транспортної задачі, а потім його послідовно покращують до отримання оптимального плану. Планом транспортної задачі буде матриця

,

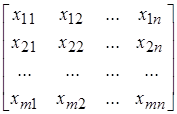в якій спостерігається баланс по рядках і стовпцях. Це відповідає вимогам обмежень задачі. Опорний план транспортної задачі буде містити (т+п–1) базисну компоненту. Система обмежень складається з (т+п) обмежень – рівнянь, однак незалежних рівнянь (m+n–1) (вимога 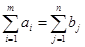робить систему залежною).

Якщо число базисних компонент менше, ніж (т+п–1), то опорний план вироджений, тоді деякі нульові компоненти необхідно вважати базисними. Їх кількість така, що базисних усього буде (т+п–1).

Опорний план може бути визначений різними способами. Наприклад, метод північно-західного кута, метод найменших елементів, метод Фогеля. Алгоритмічно визначити опорний план – це значить знайти місця розташування додатних компонент і їх величини таким чином, щоб був баланс по рядках і стовпцях (умова плану) і їх кількість була (т+п–1) (умова опірності плану).

Метод потенціалів заснований на ідеї знаходження потенціалів (величин 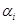і ) і 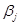виборі компоненти, що вводиться в базис, якщо опорний план неоптимальний. Для цього кожному постачальнику і кожному споживачеві ставлять у відповідність певні числа 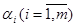, і 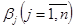, які називають відповідно потенціалами постачальників і споживачів.

Метод потенціалів базується на теоремах теорії потенціалів [24].

Теорема 1. Якщо план 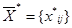транспортної задачі (ТЗ) є оптимальним, то йому відповідає система з m+n чисел α_i і β_j, яка задовольняє умови:

–α_i + β_j = c_ij для x_ij > 0 ,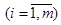

–α_i + β_j 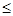c_ij для x_ij = 0 .

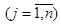Теорема 2. Якщо при підстановці компонент оптимального плану в систему обмежень вихідної задачі i-те обмеження перетворюється в нерівність, то i-та компонента оптимального плану ТЗ дорівнює нулеві.

З теореми 1 випливає, що для оптимальності опорного плану необхідне виконання таких умов:

а) для кожної заповненої клітинки (i, j), (x_ij > 0): –α_i + β_j = c_ij;

б) для кожної незаповненої клітинки (x_ij = 0): –α_i + β_j 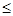c_ij, тобто

–α_i + β_j –c_ij 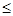0.

Алгоритм методу потенціалів є покроковим процесом, що складається з перевірки на оптимальність опорного плану, виродженість і перехід на повний опорний план. Процес керується ознакою оптимальності. Опишемо цей процес.

Крок 1. Звести дані в таблицю і визначити опорний план. Якщо план вироджений, то ввести нульові базисні елементи.

Крок 2. Скласти систему рівнянь для x_ij ≠ 0 і обчислити всі потенціали відповідно пунктів відправки і пунктів призначення α_i і β_j. Ці числа знаходять з системи рівнянь

–α_i + β_j = c_ij, (4.2.6)

де c_ij – тарифи, що стоять в заповнених клітинках таблиці умов транспортної задачі.

Оскільки кількість заповнених клітинок п+т–1, то система (4.2.6) з п+т невідомими містить п+т–1рівнянь. Оскільки кількість невідомих перевищує на одиницю кількість рівнянь, то одне з невідомих можна покласти рівним довільному числу, наприклад, α_i = 0, і знайти послідовно з рівнянь (4.2.6) значення інших невідомих. Після того, як всі потенціали визначені, для кожної вільної клітинки визначають числа

α_ij = –α_i + β_j – c_ij.

Якщо серед чисел α_ij немає додатних, то знайдений опорний план є оптимальним. В противному випадку необхідно перейти до нового опорного плану. Для цього розглядають всі вільні клітинки, для яких α_ij > 0, і серед даних чисел вибирають максимальне. Клітинку, якій це число відповідає, необхідно заповнити.

Заповнюючи вибрану клітинку, необхідно змінити об’єми поставок, записаних в ряді інших зайнятих клітинок.

Процедура переходу від одного опорного плану до іншого виконується таким чином. Нехай вибраний деякий небазисний елемент x_ij, який вводиться в базис. Відмітимо його знаком “+”. Далі будується замкнений ланцюжок вершинами якого будуть базисні елементи опорного плану. Вершини ланцюжка позначаються знаком “+” і “–” по черзі, дотримуючи правила: кожний рядок і стовпець повинні мати стільки елементів, відмічених знаком “–”, скільки “+”. Серед елементів, відмічених знаком “–” вибирається мінімальний елемент. Позначимо його через θ. θ додається до елементів відмічених знаком “+” і віднімається від елементів, відмічених знаком “–”.

Крок 3. Після цієї процедури отриманий новий опорний план перевіряємо на оптимальність, тобто знову повторюємо всі дії кроку 2.

Зауважимо, що в процесі розв’язання задачі може бути отриманий вироджений опорний план. Щоб уникнути в цьому випадку зациклювання, необхідно відповідні нульові елементи опорного плану замінити малим додатним числом Е і розв’язувати задачу як невироджену. В оптимальному плані такої задачі необхідно вважати Е рівним нулю.

Приклад.Визначимо оптимальний план транспортної задачі методом потенціалів. Вхідні дані задачі запишемо у вигляді таблиці 4.6.

Таблиця 4.6

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4
А1
А2
А3
Потреби

В першу чергу, використовуючи метод мінімального елементу, знаходимо опорний план задачі. Цей план записаний в таблицю (4.7).

Таблиця 4.7

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4
А1
А2
А3
Потреби

Складемо систему рівнянь:

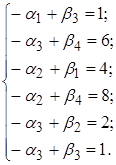
Нехай α₁ = 0. Тоді β₃ = 1, α₃ = 0, β₄ = 6, α₂ = –2, β₁ = 2, β₂ = 2.

Тепер для кожної вільної клітинки визначимо числа α_ij = α_i + β_j – c_ij:

α₁₁ = –α₁ + β₁ – c₁₁ = 0 + 2 – 7 = –5;

α₁₂ = –α₁ + β₂ – c₁₂ = 0 + 2 – 8 = –6;

α₂₂ = –α₂ + β₁ – c₂₂ = 2 + 2 – 5 = –1;

α₂₃= –α₂ + β₃ – c₂₃ = 2 + 1 – 9 = 6;

α₃₁= –α₃ + β₁ – c₃₁ = 0 + 2 – 9 = –7;

α₁₄= –α₁ + β₄ – c₁₄ = 0 + 6 – 2 = 4.

Заключаємо знайдені числа в рамки і записуємо їх відповідно в кожну вільну клітинку таблиці 4.8.

Таблиця 4.8

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4
А1
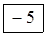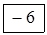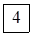А2
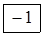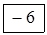А3
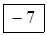Потреби

План не оптимальний, оскільки α₁₄ = 4 > 0. Потрібно компоненту 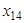ввести в базис. Побудуємо ланцюжок.

		–160	+
		+30	–90

Найменше з чисел в мінусових клітинках дорівнює 90. Отже, клітинка в якій знаходиться це число, стає вільною в новій таблиці 4.9. Інші числа в табл. 4.9 отримуються так: до чисел, що стоять в плюсових клітинках ланцюжка додамо числа, що знаходиться в мінусових клітинках з урахуванням потреб та запасів. Клітинка на перетині стрічки А₃ і стовпця В₄ стає вільною.

Після цих перетворень отримуємо новий опорний план (табл. 4.9).

Таблиця 4.9

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4
А1
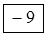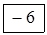А2
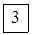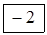А3
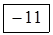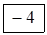Потреби

Перевіримо цей план на оптимальність. Знову знаходимо потенціали пунктів відправки і призначення. Для цього складемо таку систему рівнянь:

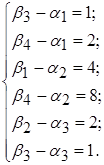
Покладемо α₁ = 0. Отримаємо: β₃ = 1, β₄ = 2, α₃ = 0, α₂ = –6, β₁ = –2, β₂ = 2.

Для кожної вільної клітинки обчислимо числа:

α₁₁ = β₁ – α₁ – 7 = – 2 – 0 – 7 = –9;

α₁₂ = β₂ – α₁ – 8 = 2 – 0 – 8 = –6;

α₂₂ = β₂ – α₂ – 5 = 2 + 6 – 5 = 3;

α₂₃ = β₃ – α₂ – 9 = 1 + 6 – 9 = –2;

α₃₁ = β₁ – α₃ – 9 = – 2 – 0 – 9 = –11;

α₃₄ = β₄ – α₃ – 6 = 2 – 0 – 6 = –4.

В даному випадку α₂₂ = 3 > 0, отже опорний план не є оптимальним. Побудуємо ланцюжок.

		–70	+90
	+		–20
	–50	+120

Найменше з чисел у мінусових клітинках дорівнює 20 і його запишемо у клітинку А₂В₂. Отже клітинка, в якій знаходилось це число, стає вільною у новій таблиці 4.10. Інші числа у таблиці 4.11 отримуються так: до числа 90 додаємо 20 і одночасно від числа 70 віднімаємо 20 і додаємо його до числа 120 та віднімаємо число 20 від 50. Після цих перетворень отримуємо новий опорний план (табл. 4.10). Перевіримо цей план на оптимальність. Знову знаходимо потенціали пунктів відправки і призначення. Для цього складемо таку систему рівнянь:

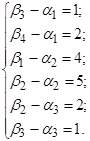
Покладемо α₁=0. Отримаємо: β₃ = 1, β₄ = 2, α₃ = 1 – 1 = 0, β₂ = 2 – 0 = 2,

α₂ = –3, β₁ = 7.

Для кожної вільної клітинки обчислимо числа:

α₁₁ =β₁ – α₁ – c₁₁ = 7 – 0 – 7 = –6;

α₁₂ = β₂ – α₁ – c₁₂ = 2 – 0 – 8 = –6;

α₂₃ = β₃ – α₂ – c₂₃ = 1 + 3 – 9 = –5;

α₂₄ = β₄ – α₂ – c₂₄ = 2 + 3 – 8 = –3;

α₃₁ = β₁ – α₃ – c₃₁ = 7 – 0 – 9 = –2;

α₃₄ = β₄ – α₃ – c₃₄ = 2 – 0 – 6 = –4.

В даному випадку всі α_ij < 0 і опорний план є оптимальний.

Таблиця 4.10

Пункти відправлення	Пункти призначення	Запас
В1	В2	В3	В4
А1
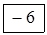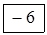А2
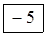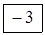А3
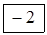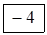Потреби

Сумарні транспортні витрати:

f = 1·50 + 2·110 + 4·120 + 5·20 + 2·30 + 1·140 = 1050.

Отже, отримуємо такий оптимальний план:

.

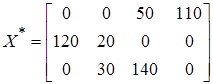Стержневі системи

Загальні положення

Розглянемо конструкцію з плоскої шарнірно-стержневої ферми (рис. 5.1). Будемо вважати, що стержні ферми не мають попередньої напруженості, а зовнішні навантаження у вигляді сил R_к прикладені у вузлах.

Сили завантаження F₂ і F₃, діючі в навантаженнях па типовий елемент е₂, подамо у вигляді проекцій 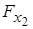, , 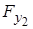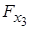і 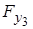, відповідно, (рис. 5.1,а).

Зміщення вузлів елемента від їх початкового положення (без зусиль діючих на ферму) позначимо відповідно через , , , .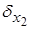

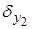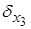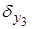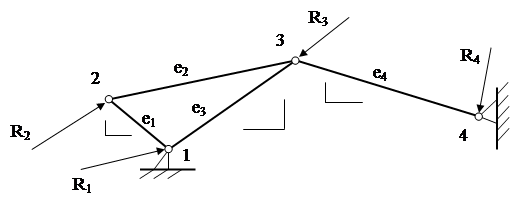
Рисунок 5.1

Розтяг або стиск стержня незавантаженої довжини L визначається величиною 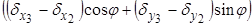і деформація отримається в результаті ділення цієї величини на L. Оскільки напруження дорівнює модулю Юнга Е = [Н/м², (кГ/см²)] помноженому на деформацію, то повздовжня сила, яка прикладена до стержня (рис. 5.1, а) описується виразом

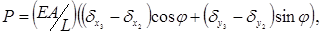(5.1.1)

де А – площа поперечного перерізу стержня.

Компоненти повздовжньої сили Р можуть бути прирівняні до компонент шарнірних сил:

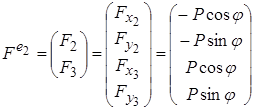. (5.1.2)

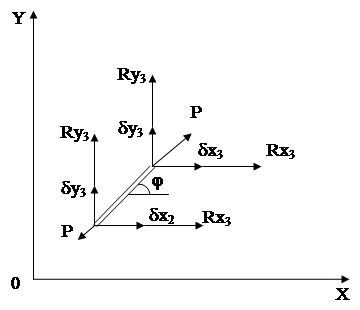Рисунок 5.1, а

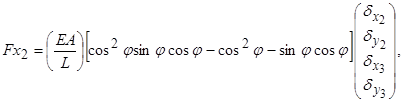(5.1.3, а)

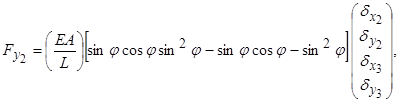(5.1.3, б)

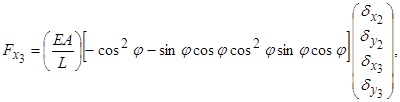(5.1.3, в)

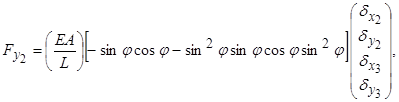(5.1.3, г)

Одержані рівняння (5.1.3) запишемо у такому вигляді:

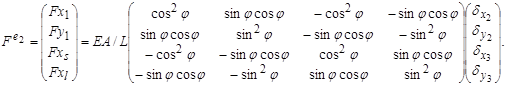(5.1.4)

Рівняння (5.1.4) є матричне рівняння для елемента е₂(узагальнений закон Гука) і його квадратна матриця коефіцієнтів з множником EA/L називається матрицею жорсткості К₂даного елемента [15]. Аналогічні рівняння можуть бути отримані і для інших елементів.

Рівняння (5.1.4) може бути розширене так, щоб воно включало всі вузлові зміщення системи. Для цього необхідно розширити (проасемблювати) матрицю жорсткості з використанням необхідної кількості нулів. Порядок розширеної матриці К₂ дорівнює подвійному добутку кількості вузлів конструкції. Так для стержневої системи (рис. 5.1) розмірність розширеної матриці dim K=8х8.

В результаті маємо:

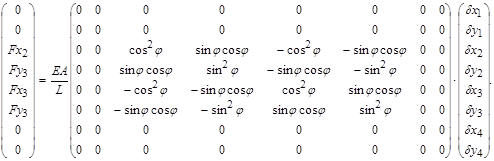(5.1.4, а)

Зовнішні сили R₁, R₂, R₃, R₄ виражаються через х, у – компоненти 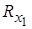, ,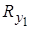…, , 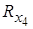, 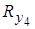а умова рівноваги в вузлових точках може бути визначена через ці компоненти. Наприклад, у вузлі 2 умова рівноваги в напрямку х має вигляд

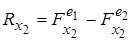. (5.1.5)

Ясно, що вклад в праву частину (5.1.5) дають тільки ті елементи, які включають вузол 2, але зручно записати (5.1.5) в такому вигляді:

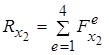. (5.1.5, а)

Аналогічне співвідношення отримується для другої компоненти вектора R₂:

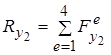. (5.1.5, б)

Рівняння (5.1.5, а) і (5.1.5, б) можна об'єднати в матричний запис:

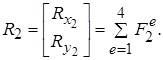(5.1.6)

Аналогічні рівняння можна записати і для інших вузлів. Підсумкова система рівнянь рівноваги запишеться так:

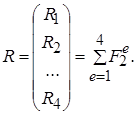(5.1.7)

Підстановка виразів типу (5.1.4) в рівняння (5.1.7) дає

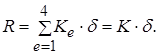(5.1.8)

де К – матриця жорсткості системи, δ – вектор вузлових зміщень системи.

Формула (5.1.8) дає можливість обчислити зміщення і реакції вузлів.

Стержневі системи

Деяка сукупність стержнів, які мають певні вузли, становить стержневу систему [6]. В інженерній практиці конструкторів завжди цікавить важливе питання, чи буде стержнева система в рівновазі. На це питання дає відповідь математична модель стержневої системи, яка будується на основі системного аналізу. Всі теоретичні положення будемо розглядати на основі стержневої системи, яка зображена на рисунку 5.2.

Система складається з чотирьох стержнів: L₁, L₂, L₃, L₄, які мають відповідно площі поперечного перерізу А₁, А₂, А₃, А₄. Стержні мають вузли, які ми занумерували вузлами 1, 2, 3 та 4. Всі стержні виготовлені з одного матеріалу, модуль Юнга якого – Е.

Стержень L₁ утворює з віссю ОХ кут φ₁=150^о, стержень L₂ паралельний осі ОХ, стержень L₃ утворює з віссю ОХ кут φ₃=126,874^о, стержень L₄ утворює з віссю ОХ кут φ₄=53,127^о.

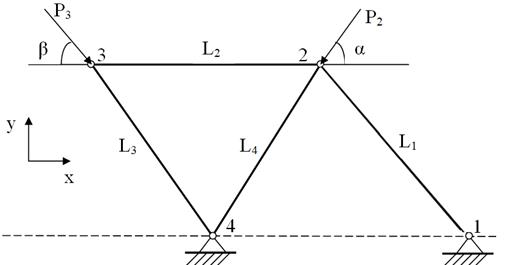
Рисунок 5.2

Алгоритм формування математичної моделі даної системи такий:

1. Обчислюємо матриці жорсткості для кожного стержня за формулою (5.1.5):

а) стержень L₁ утворює з віссю ОХ кут φ₁=150^о.

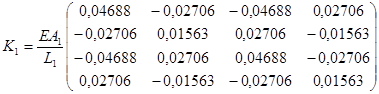. (5.2.1, а)

б) стержень L₂ утворює з віссю ОХ кут φ₂=0^о.

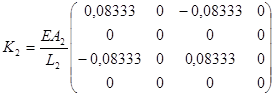. (5.2.1, б)

в) стержень L₃ утворює з віссю ОХ кут φ₃=126,874^о.

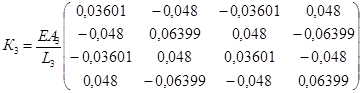. (5.2.1, в)

г) стержень L₄ утворює з віссю ОХ кут φ₄=53,127^о.

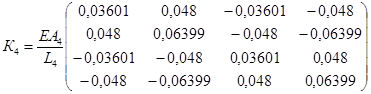. (5.2.1, г)

2. Задаємо конкретні величини: Е=2×10¹² кГ/см²; А₁=А₂=А₃=А₄= =0,5 дм²; L₁=8 м; L₂=6 м; L₃=L₄=5 м (округлено для спрощення подальших розрахунків). І підставляємо їх у формули 5.2.1, а; 5.2.1, б; 5.2.1, в; 5.2.1, г.

3. Формуємо дві загальні матриці реакції та зміщення вузлів. Маємо 4 вузли. Отже, маємо 8 реакцій та 8 зміщень:

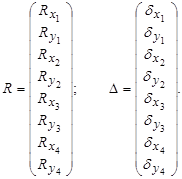(5.2.2)

Найважливішою механічною властивістю стержневої системи є те, що поведінка системи описується узагальненим законом Гука:

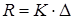. (5.2.3)

У формулі (5.2.3) dim R = 8×1. Тоді виникає така розмірність

dim K = 8×8. (5.2.4)

Тепер основна проблема полягає в тому, щоб отримати матрицю К знаючи 4 матриці К₁, К₂, К₃ та К₄. Цю проблему розв’язує процес асемблювання матриць.

Запишемо формулу (5.2.3) в розгорнутому вигляді:

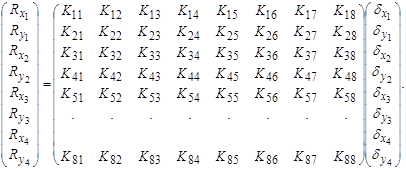(5.2.5)

Формула (5.2.5) повинна збігатись з формулою (5.1.6) для стержня L₁. А це означає, перші чотири рядки матриці К₁ повинні залишатись без зміни, а решта елементів нулі. Аналогічно будемо міркувати для стержнів L₂, L₃ та L₄.

4. Асемблювання матриць.

Для збереження закону Гука ми повинні зберегти матрицю К₁, а решту елементів прирівняти до нуля.

Пунктиром окреслена матриця К₁. Матриця К₁ не містить вузла 3 та вузла 4.

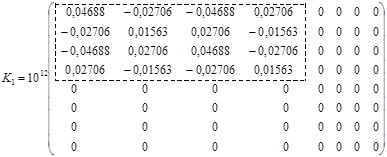. (5.2.6, а)

Матриця К₂ не містить вузла 1 та вузла 4.

Отже будемо мати:

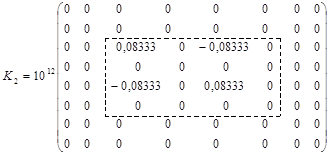. (5.2.6, б)

Матриця К₃ не містить вузла 1 та 2. Отже отримаємо:

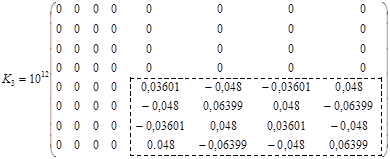. (5.2.6, в)

Наголосимо, що стержень L₄ містить вузол 2 та 4, а не містить вузол 1 та 3. Вузлу 1 відповідають перший та другий рядки, які будуть нулями та п’ятий і шостий рядки – теж нулі. Маємо:

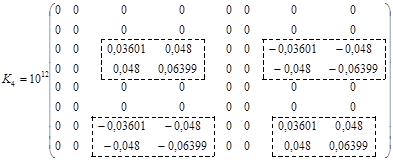. (5.2.6, г)

5. Формування загальної матриці жорсткості стержневої системи відбувається за формулою (5.2.7):

R=åK_i, i= 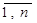. (5.2.7)

У формулі (5.2.7) К_і – асембльовані матриці. Для нашого прикладу маємо:

К = К₁+К₂+К₃+К₄. (5.2.7, а)

Наголосимо, що при виконанні додавання перед дужкою у матрицях повинні бути однакові множники. Маємо:

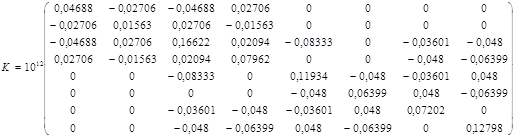. (5.2.7, б)

6. Граничні умови. На рисунку 5.2 маємо:

а) вузли 1 та 4 закріплені наглухо. Отже, ;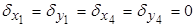

б) на вузол 2 діє сила Р₂ = 1000 кг під кутом a = 60^о, а на вузол 3 діє сила Р₃ = 2000 кг під кутом b = 30^о.

Знаки проекцій вибираємо згідно з рисунком 5.3 та 5.4. Маємо:

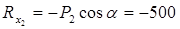(кГ);

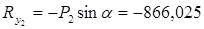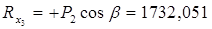(кГ);

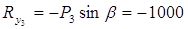(кГ);

(кГ).

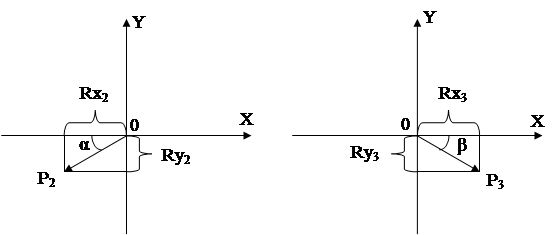
Рисунок 5.3 Рисунок 5.4

За формулою (5.2.5) формулюємо матричну модель стержневої системи, зображеної на рис.5.2.

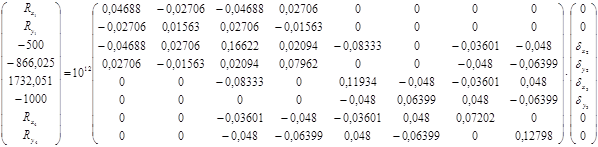
(5.2.8)

Формула (5.2.8) становить математичну модель стержневої системи, зображеної на рис. 5.2.

1. Нам відомі реакції вузла 2 та 3. Отже, нам потрібно розв’язувати систему рівнянь:

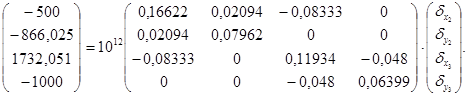(5.2.9)

2. Розглядаючи (5.2.9) як систему вигляду АХ=В та розв’язуючи її за методом Гауса маємо:

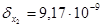(см);

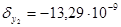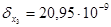(см);

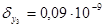(см);

(см).

3. Враховуючи (5.2.10) обчислимо реакції нерухомих вузлів згідно з формулою (5.2.8):

а) 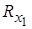знаходимо в першому порядку

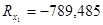(кГ);

б) 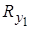знаходимо в другому порядку

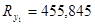(кГ);

в) 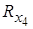знаходимо в сьомому порядку

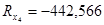(кГ);

г) 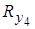знаходимо в восьмому порядку

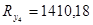(кГ).

4. Контроль.

Якщо знайдені розв’язки математичної моделі (5.2.8) правильно, то стержнева система повинна знаходитись у рівновазі.

Отже, повинно виконуватись дві рівності:

1. ;

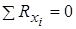2. .

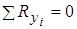Перевірка:

а) ;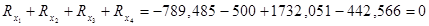

б) .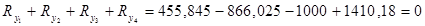

Отже, для математичної моделі (5.2.8) розв’язки знайдено правильно.

Електричні системи

Основні положення

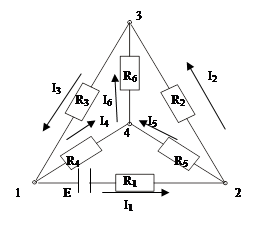
Рисунок 6.1

Електрична система складається з батареї з електрорушійною силою Е, ребер провідників (провідників з опором R_k), по яких тече електричний струм І_k, та вузлів.

Приклад такої системи показано на рисунку 6.1 [14]. Нумеруємо вузли. На ребрах довільним чином задаємо напрям електричних струмів І_k.

Для формування математичної моделі застосуємо два закони Кірхгофа, які виразимо мовою матричної алгебри. Відзначимо, що вони базуються на теорії графів, тобто залежать лише від способу з'єднання вершин ребрами і від напрямку стрілок, але не залежать від величин опору (або потужностей батарей) в контурі. Зв'язки між вершинами повністю описуються матрицею інцидентності графу цього контура, яка має рядок для кожної вершини або замкнутого контура і стовпець для кожного ребра. В кожному стовпці цієї матриці два ненульових елемента +1 і –1 відмічають початкову і кінцеву вершину ребра.

Графом називають сукупність вершин (вузлів) і зв'язуючих їх ребер (ланок). Визначення графу може бути записане в такому вигляді:

Г = (У, Р, І),

де У – множина вершин; Р – множина ребер; І – інцидентор (показник способу з'єднання ребер одне з одним).

Якщо для ребер графу вказані конкретні напрямки, то граф називають направленим графом (орієнтованим або орграфом), ребра направленого графу називають дугами.

Маршрутом називають послідовність S ребер, в якій сусідні ребра інцидентні одній і тій же вершині. Термін "інцидентність" означає співвідношення об'єктів типу "проходить через..." або "знаходиться на...". На рис. 6.2 в графі послідовності (b, c, e, f, c, d) і (e, g) – маршрути, але (a, h) не маршрут, тому що ребра а і h інцидентні різним вершинам. Якщо в маршруті немає ребер, які повторюються, то маршрут називають ланцюгом. Якщо ланцюг починається і закінчується в одній і тій же самій вершині, то маємо цикл – контур. Кількість ребер в ланцюгу називають довжиною маршруту.

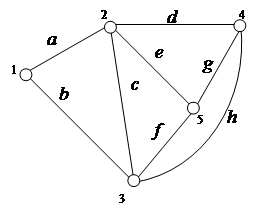Рисунок 6.2

Зв'язним графом називають граф, у якому можна вказати маршрут, що зв'язує будь-які вершини.

Деревом зв'язного графу називають зв'язний підграф без циклів.

За допомогою матриці інцидентності А=[a_і,j] може бути виражена інформація, яка міститься у графі. В цій матриці β–1 рядків і α стовпців. Кожному вузлу за винятком одного, який приймається за базовий, в матриці відповідає один рядок; а кожному ребру один стовпець. В стовпці записуються одиниці на перетині з рядками тих вузлів, якому інцидентне ребро даного стовпця. Якщо граф направлений, то знаки одиниць вказують напрям дуг: +1 відповідає рядок вузла, до якого направлене ребро, –1 рядок другого вузла. В клітинках матриці, які залишилися, записуються нулі. Наприклад, матриця інцидентності для графу рис. 6.3 у випадку, коли базовим вузлом є вузол 4, подана у таблиці 6.1.

Рисунок 6.3

Таблиця 6.1