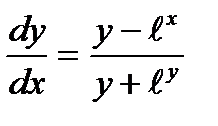Жұп және тақ функциялар. 3. Жұп және тақ функциялар.

а) 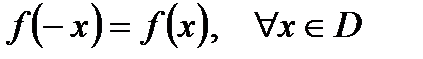болса, 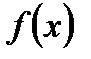- жұп функция;

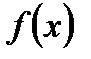б) болса, - тақ функция.

Егер функцияның анықталу облысындағы кез келген х үшін f(-x)=f(x)

теңдігі орындалса функция жұп деп, ал f(-x)=-f(x) теңдігі орындалса функция тақ деп аталады. Мысалы, y=x²ⁿ, y=|x| функциялары жұп, ал y=x²ⁿ⁺¹, функциялары тақ болады.

Жұп функция графигі Оу осіне, ал тақ функция графигі О(0,0) – координаталар басына қарағанда симметриялы болады.

Жұп функциялардың қосындысы, айырымы, көбейтіндісі, бөліндісі - жұп функция болады.

Тақ функциялардың қосындысы мен айырымы - тақ, ал көбейтіндісі мен бөліндісі - жұп функция болады.

Егер функция үшін f(-x)=f(x) жәнеf(-x)=-f(x)теңдіктерінің екеуі де орындалмаса функция жұп та, тақ та емес (бейтарап) болады. Мысалы, y=x²+х функциясы жұп та, тақ та емес.

57. Периодты функциялар. Периодты функциялар. облысында анықталған 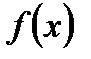фукциясы үшін саны табылып, 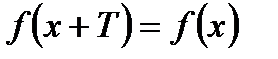, , теңдігі орындалса, онда 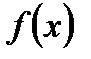периодты функция деп аталады.

Егер функцияның анықталу облысындағы кез келген х үшін

f(x+Т)=f(x) теңдігі орындалатындай Тсан табылса функция периодты деп аталады. Осындай Тсандардың ең кішісі функцияның негізгі периоды деп аталады. Мысалы, y=sin(x), y=cos(x)(бұлардың негізгі периоды 2 ), y=tg(x), y=ctg(x) (бұлардың негізгі периоды ) - периодты функ.

4. Бірсазды (монотонды) функциялар. Егер функцияның анықталу облысындағы кез келген х₁, х₂ (х₁< х₂) мәндер үшін

f(х₁)< f(х₂) теңсіздігі орындалса, функция өспелі(3 а-сурет),

f(х₁) > f(х₂) теңсіздігі орындалса, функция кемімелі(3 б-сурет),

f(х₁) 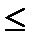f(х₂)теңсіздігі орындалса, функция кемімейтін(3 в-сурет),

f(х₁) 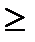f(х₂) теңсіздігі орындалса, функция өспейтін (3 г-сурет)

деп аталады.

х

у

х

у

х

у

х

у

3 а-сурет 3 б-сурет 3 в-сурет 3 г-сурет

Егер қандай да бір аралықта функция не тек өспелі немесе тек кемімелі болса, оны осы аралықта монотонды (бірсазды) деп айтады.

58. Күрделі функция.1. Шенелген функция. Егер функцияның анықталу облысындағы кез келген х үшін қандай да бір М нақты сан табылып f(x)<M теңсіздігі орындалса функция жоғарыдан шенелген, ал f(x)>M теңсіздігі орындалса функция төменнен шенелген деп аталады (2 а,б-сурет) .

Егер функцияның анықталу облысындағы кез келген х үшін қандай да бір М нақты сан табылып |f(x)|<M теңсіздігі орындалса функция шенелген деп аталады (2 в-сурет).

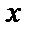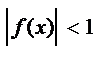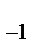2 а-сурет 2 б-сурет 2 в-сурет

2. Жұп және тақ функция. Егер функцияның анықталу облысындағы кез келген х үшін f(-x)=f(x)

теңдігі орындалса функция жұп деп, ал f(-x)=-f(x) теңдігі орындалса функция тақ деп аталады. Мысалы, y=x²ⁿ, y=|x| функциялары жұп, ал y=x²ⁿ⁺¹, функциялары тақ болады.

Жұп функция графигі Оу осіне, ал тақ функция графигі О(0,0) – координаталар басына қарағанда симметриялы болады.

Жұп функциялардың қосындысы, айырымы, көбейтіндісі, бөліндісі - жұп функция болады.

Тақ функциялардың қосындысы мен айырымы - тақ, ал көбейтіндісі мен бөліндісі - жұп функция болады.

Егер функция үшін f(-x)=f(x) жәнеf(-x)=-f(x)теңдіктерінің екеуі де орындалмаса функция жұп та, тақ та емес (бейтарап) болады. Мысалы, y=x²+х функциясы жұп та, тақ та емес.

3. Периодты функциялар. Егер функцияның анықталу облысындағы кез келген х үшін

f(x+Т)=f(x)теңдігі орындалатындай Т сан табылса функция периодты деп аталады. Осындай Т сандардың ең кішісі функцияның негізгі периоды деп аталады. Мысалы, y=sin(x), y=cos(x) (бұлардың негізгі периоды 2 ), y=tg(x), y=ctg(x) (бұлардың негізгі периоды ) - периодты функ.

4. Бірсазды (монотонды) функциялар. Егер функцияның анықталу облысындағы кез келген х₁, х₂ (х₁< х₂) мәндер үшін

f(х₁)< f(х₂)теңсіздігі орындалса, функция өспелі(3 а-сурет),

f(х₁) > f(х₂) теңсіздігі орындалса, функция кемімелі(3 б-сурет),

f(х₁) 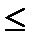f(х₂)теңсіздігі орындалса, функция кемімейтін(3 в-сурет),

f(х₁) 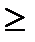f(х₂) теңсіздігі орындалса, функция өспейтін (3 г-сурет)

деп аталады.

х

у

х

у

х

у

х

у

3 а-сурет 3 б-сурет 3 в-сурет 3 г-сурет

Егер қандай да бір аралықта функция не тек өспелі немесе тек кемімелі болса, оны осы аралықта монотонды (бірсазды) деп айтады.

5. Кері функция. y=f(x) функциясының кері функциясын табу үшін алдымен х аргументті у айнымалы арқылы өрнектейміз, х=g(у), одан кейін, тәуелсіз аргумент х деп ал ал тәуелді айнымалы у деп белгілеу қалыптасқандықтан, алынған өрнектегі х пен у орындарын алмастырамыз, у=g(х). Пайда болған g(х) функция берілген f(x) функцияға кері функцияболады.

Өзара кері функциялардың графигі y=x (бірінші және үшінші декарттық бұрыштардың биссектрисасы) түзуіне қарағанда симметриялы болады.

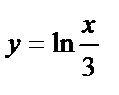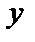4-сурет

Мысалы,

4-сурет

функциясының кері функциясын табау керек (4-сурет). Шешуі. Алдымен теңдеудегі х аргументті у айнымалы арқылы өрнектеу үшін х-ке қатысты шешеміз:

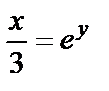осыдан .

Енді алынған өрнектегі х пен у орындарын алмастырамыз: .Сонда берілген ф-ға кері функция болады.

Берілген функцияның анықталу облысы оған кері функцияның мәндер жиыны болады да, мәндер жиыны кері функцияның анықталу облысы болады.Аралықта монотонды өсетін немесе монотонды кемитін функциялардың ғана кері функциялары табылады.

6. Күрделі функция. y=f(g(x)) түрінде берілген функцияны күрделі функция дейді. Кейде күрделі функцияны мынадай түрде де береді: y=f(u) мұндағы u=g(x). Бұл жағдайда u - аралық айнымалы, ал х -тәуелсіз аргумент болады.

Мысалы, 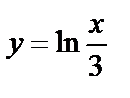ф-сы күрделі функция. Оны , мұндағы 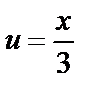түрінде жазуға болады.

7. Айқын емес түрде берілген функция. Егер функция F(x,y)=0, яғни y айнымалыға қатысты шешілмеген түрінде, берілсе функция айқын емес түрде берілген дейміз. Жоғарыда қарастырылған 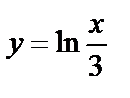функцияны айқын емес түрде былай жазамыз: .

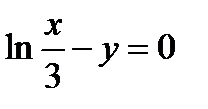59. Кері функция.Кері функция. y=f(x) функциясының кері функциясын табу үшін алдымен х аргументті у айнымалы арқылы өрнектейміз, х=g(у), одан кейін, тәуелсіз аргумент х деп ал ал тәуелді айнымалы у деп белгілеу қалыптасқандықтан, алынған өрнектегі х пен у орындарын алмастырамыз, у=g(х). Пайда болған g(х) функция берілген f(x) функцияға кері функцияболады.

Өзара кері функциялардың графигі y=x (бірінші және үшінші декарттық бұрыштардың биссектрисасы) түзуіне қарағанда симметриялы болады.

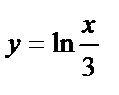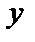4-сурет

Мысалы,

4-сурет

функциясының кері функциясын табау керек (4-сурет). Шешуі. Алдымен теңдеудегі х аргументті у айнымалы арқылы өрнектеу үшін х-ке қатысты шешеміз:

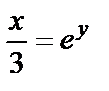осыдан .

Енді алынған өрнектегі х пен у орындарын алмастырамыз: .Сонда берілген ф-ға кері функция болады.

Берілген функцияның анықталу облысы оған кері функцияның мәндер жиыны болады да, мәндер жиыны кері функцияның анықталу облысы болады.Аралықта монотонды өсетін немесе монотонды кемитін функциялардың ғана кері функциялары табылады.

60. Айқындалмаған функция. Айқындалмаған функция және оның туындысы.

Айталық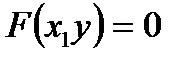теңдеуі берілсін. Мұнда х-тен тәуелді функция. Бұл жағдайда айқындалмай берілген функция дейді.(8.3) формуланы пайдаланып (8.9) теңдеуді шығарамыз. Осыдан

(8.10) айқындап берілмеген функцияның туындысы.

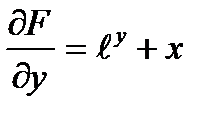Мысалы: теңдеуі берілсін. Мұнда онда