Радиоприемные устройства дискретных сигналов 4 страница

Если x/t₀ 4; 1,то процесс модуляции можно рассматривать как статический, т. е. в промежутке t₀ амплитуду и фазу ЧМ-колебания на выходе линейной цепи можно определять методом комплексных амплитуд (по АЧХ и ФЧХ), как в стационарном режиме. Общее решение методом мгновенной частоты изложено в [11].

Применим указанный метод к оценке нелинейных искажений при гармонической ЧМ. Пусть мгновенная частота

cu(tf) = co₀-f Aco_flcosQ/. (15.66)

Согласно методу мгновенной частоты в квазистационарном приближении выходное напряжение линейной цепи с передаточной функцией К (И

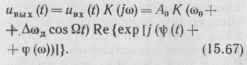
Здесь ы_вх (г) — входное ЧМ-колеба-ние; i|> (г) = u)₀t + т sin Qr — его полная фаза; ср (со) — ФЧХ цепи.

Амплитуда выходного напряжения (15.67) изменяется по закону U {t) = А_и К (со„ f Дсод cos Qt), а мгновенная частота

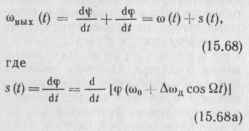
— слагаемое, характеризующее влияние ФЧХ на изменение мгновенной частоты выходного колебания. При настройке цепи на среднюю частоту ЧМ-сигнала ы_й с учетом симметричности ФЧХ относительно со,, частота (15.68 а) может быть разложена в ряд Фурье, который содержит лишь

нечетные гармоники частоты модуляции (2н ¹ 1) Q, п ~ 0, 1,2,...:

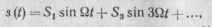(15.69)

где S,, S_a, ... — амплитуда гармоник функции s (t). Подставляя ряд (15.69) в (15.68), получаем

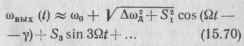
Сравнивая закон изменения частоты для входного (15.66) и выходного (15.70) ЧМ-сигналов, замечаем, что влияние избирательных цепей линейной части приемника вызывает не-, большое изменение амплитуды частотного отклонения и запаздывание фазы основной частоты модуляции Q на угол у да arctg (Si/АсОд),а также возникновение нечетных гармоник сообщения в законе изменения мгновенной частоты. Это и есть нелинейные искажения сообщения, проявляющиеся на выходе частотного детектора.

Таким образом, чтобы рассчитать нелинейные искажения ЧМ-сигнала в линейных цепях приемника, необходимо записать ФЧХ ср (со),взять производную по времени dtp/dr = = S(t), и разложить ее в ряд Фурье, определив амплитуды гармоник 5_2п+| (я = 0,1,2 ...).

Коэффициент нелинейных искажений определяется соотношением

(15.71)

Приведем результаты расчета коэффициента нелинейных искажений для 3-й гармоники при прохождении ЧМ-колебаний через одиночный колебательный контур:

(15.72)

где т = Асо д/Q.

При Ло)_дт„. 1 формула (15.72) упрощается и принимает вид к₃ да да (Асо_дт„)³/4т. Для «-каскадного усилителя с одиночными контурами к<^л> пи-., да п (Аш_дт„)^яАт.

При воздействии на приемник мешающего ЧМ-сигнала со спектром, находящимся вне полосы пропускания приемника, могут возникнуть перекрестные искажения полезного сигнала из-за нелинейности вольт-амперных характеристик активных приборов. Коэффициент частотных (фазовых) перекрестных искажений определяется отношением перекрестной и полезной модуляций сигнала: Кпер = Афиер/Афг- ^Так- Д-™избирательной системы в виде одиночного колебательного контура перекрестная модуляция возникает из-за воздействия напряжения помехи на изменение активной и реактивной составляющих проводимости электронного прибора, что соответственно вызывает изменение добротности AQ и емкости ДС_К контура.

Коэффициент перекрестной модуляции 1101

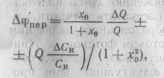
где Q и С_к — добротность и емкость контура.

Еще одной причиной нелинейных искажений является возникновение паразитной амплитудной модуляции при прохождении ЧМ-сигнала через избирательные цепи (рис. 15.16) с криволинейными фазовыми характеристиками. При точной настройке линейной части приемника на среднюю частоту ЧМ-сигнала амплитуда его на выходе избирательной цепи изменяется с удвоенной частотой модуляции. Если же в приемнике имеется некоторая расстройка по частоте, то амплитуда сигнала еще больше искажается и появляются нелинейные искажения также на основной частоте модуляции. Естественно, что при детектировании все эти искажения выявляются в выходном сигнале. Для устранения влияния паразитной AM в демодуляторах ЧМ-сигналов используют амплитудный ограничитель, предшествующий частотному детектору.

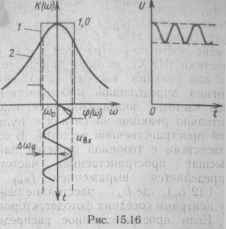
Линейные искажения ЧМ-сигнала связаны с тем, что амп литуды боковых составляющих спек ра при прохождении их через избир тельные цепи уменьшаются, что экв; валентно уменьшению индекса мод ляции. Расчет линейных искажен! производят как спектральным мет дом (при т < 1), так и методом мгн венной частоты (т )>• 1). Нетрудно п пять, что если ЧМ-колебание проход! через усилитель с идеальным полос вым фильтром (график / на рис. 15.И у которого АЧХ К (со) равномерна полосе Дсо, занимаемой спектром си нала (Дсо > 2А(о_д), а ФЧХ ст (со) л нейна в пределах той же полосы, ; амплитуды всех k-x спектральных с ставляющих сигнала получат один ковое усиление и линейный сдвиг ф &Ф,,где ф,— фазовый сдвиг nepei боковой частоты относительно нес щей. Таким образом, в этом случ происходит лишь запаздывание времени, а линейные искажения с сутствуют.

Когда же избирательная цепь с личается от идеальной, возникают л нейные искажения. Поясним это ¹ примере прохождения ЧМ-колеб ния через резонансный усилитель одиночным колебательным контур! (на рис. 15.16, график 2), у которо уравнение нормированной АЧХ их ет вид п ■ \1у 1 4- а|_к, где а_як

2A<o<<Wto₀ — обобщенная расстройка контура.

В случае узкополосной гармонической ЧМ (т — Дид/Q С 1) колебание, прошедшее через резонансный усилитель, описывается выражением

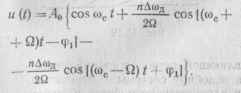
Следовательно, амплитуды частотного отклонения (девиации Дсо_д) у боковых частот ослабляются в п раз, т. е. происходят линейные искажения, а фаза модуляции запаздывает на угол Ф = arctg а-_лк. Вместе с тем закон изменения мгновенной частоты to (t) сохраняется неизменным, т. е. нелинейные искажения отсутствуют.

Аналогично может быть произведен расчет ослабления девиации частоты для каждой из частот спектра ЧМ-колебания и при т > 1.

§ 15.6. Приемники ЧМ-сигнала с обратным управлением

Техника приема ЧМ-сигналов непрерывно совершенствуется в направлении повышения помехоустойчивости в условиях воздействий на приемники достаточно больших помех, при которых помехоустойчивость обычных (некогерентных) приемников ЧМ-сигналов падает. Таким образом, инженерная мысль работает над эвристическими методами снижения пороговых областей приема ЧМ-сигнала (см. § 15.4).

Идея повышения помехоустойчивости ЧМ-приемников заключается в более полном использовании свойств ЧМ-сигнала. Рассматривая частотно-временную плоскость — со, /, изобразим на ней закон изменения частоты во времени (рис. 15.17) для простейшего случая гармонической ЧМ. Если закон ЧМ априорно известен и в момент времени t_t мгновенная частота принимает значение со (г,), то с высокой вероятностью можно записать пределы значений мгновенной частоты в момент времени t_x -f Дг:

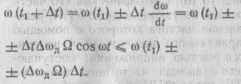
Из этого выражения следует, что можно создать устройство типа узкополосного линейного фильтра с регулируемой средней частотой, которое следило бы за мгновенной частотой принятого ЧМ-сигнала (см. рис. 15.17). Важно, что при таком приеме полоса пропускания следящего фильтра должна воспроизводить полезный сигнал, спектр модулирующих частот которого ограничивается максимальной частотой F_max. Поэтому необходимо, чтобы полоса пропускания фильтра ДГф > 2/^г_тах. Вспомним, что в обычном некогерентном приемнике (см. § 15.4, рис. 15.10) ширину полосы пропускания УПЧ выбирали, исходя из ширины спектра частот, занимаемого ЧМ-сигналом, при этом ДТупч > 2(1 -т т) F_max.

Очевидным преимуществом приемника со следящим фильтром является значительное уменьшение мощности шумов, поступающих на вход демодулятора. Уменьшение шумов можно оценить через отношение полос пропускания ДГупч/ДТф « (1 ^; т), т.е. приблизительно в индекс модуляции раз, что обеспечивает повышенную помехоустойчивость приема, выражающуюся в снижении критического порогового уровня.

Далее рассмотрим несколько способов структурной реализации следящих приемных систем.

Приемник со следящей настройкой (рис. 15.18). Специфическая его часть состоит из узкополосного УПЧ, резонансная частота которого с помощью управляемого элемента (УЭ) изменяется частью напряжения, поступающего с выхода частотного детектора (ЧД) через ФНЧ, придающий управлению избирательный характер. Переменная составляющая со_р^, резонансной частоты следящего УПЧ связана с переменной составляющей ш_х^, колебательного процесса в УПЧ соотношением со„_. = К„ы_х^, где

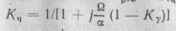— передаточная функция частотной девиации, т. е. отношение комплексных амплитуд частотной девиации ЧМ-колебания на следящем фильтре к частотной девиации ЧМ-сигнала на его входе; а = R/2L — коэффициент затухания узкополосного УПЧ; К_у— комплексный коэффициент передачи тракта управления резонансной частотой следящего фильтра, включающего в себя ЧД, ФНЧ и УЭ. Зависимость \К_Ч\ от Q называется эквивалентной частотной характеристикой следящего фильтра и имеет вид, показанный на рис. 15.19, где т_у — постоянная времени эквивалентной уп-

равляющей цепи. Основной недостаток подобной системы — относительная сложность устройства и возможность потери входного сигнала, если оценка частоты на выходе ФНЧ неверна.

Приемник с отрицательной обратной связью по частоте (рис. 15.20). Эффекта следящего УПЧ можно достигнуть иным способом, используя обратную связь по частоте (ОСЧ). Напряжение с выхода ЧД подается через фильтр нижних частот (ФНЧ) и управляемый элемент (УЭ) на управляемый генератор (УГ), осуществляя его частотную модуляцию. При этом знак модуляции УГ соответствует знаку полезного ЧМ-сигнала.

«Частота покоя» УГ, соответствующая нулевому значению напряжения на его выходе, сдвинута относительно средней частоты со_пЧМ-сигнала на величину со,,.

Напряжение УГ можно записать в виде

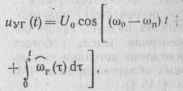(15.73)

где со7 (г) — оценка частоты гетеродина.

юв*

Ш

В результатевоздействия на смеситель(См) двух синфазно-модулиро-ванных сигналов:

от УРЧ u_s(t) = A₀sm [co₀t +

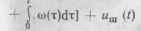и от УГ [см.

(15.73)1 образуется сигнал со средней частотой ш_п, модулируемый по частоте сигналом ошибки, допускаемой при оценке мгновенной частоты входного сигнала:

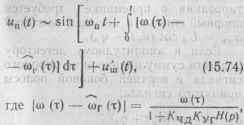
Кчц, /Cyi— коэффициенты передачи ЧД и УГ; Н (р) — передаточная функция ФНЧ.

Из выражения (15.74) следует, что частотное отклонение входного ЧМ-сигнала уменьшается системой ОСЧ в 1+ Кчд Куг Н (р) раз, так что перед ЧД можно поставить узкополосный УПЧ с фиксированной настройкой, который должен без искажений фильтровать полезные сигналы в полосе ДТупч > 2/⁷_тах и режектиро-вать все остальные частоты. Сигнал с выхода узкополосного УПЧ подается на амплитудный ограничитель (АО) и ЧД, выходное колебание которого складывается из напряжения, пропорционального ошибке «чд ft

*= Кчд |со (/) — ш_г (г)|, и шумов. Последние влияют на точность оценки частоты, поэтому в петле регулирования всегда существует сигнал ошибки, вводящий систему в режим синхронизации по частоте. По аналогии со следящим фильтром для приемника с ОСЧ можно ввести эквива-

лентную передаточную функцию как отношение комплексных амплитуд частотных отклонений напряжения УГ и входного сигнала:

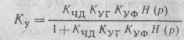
Таким образом, введение ОСЧ приводит к сжатию спектра входного сигнала, что способствует у пию шума на входе ЧД и снижению пороговой области ЧМ-приема.

Приемник с ФАПЧ (рис. 15.21). Особенность его состоит в том, что узкополосность приемного тракта создается только по низкой частоте — с помощью фильтра ФНЧ. На фазовый детектор (ФД) подаются два напряжения — управляемого гетеродина (УГ) с мгновенной фазой 9 (/), являющейся оценкой мгновенной фазы принимаемого ЧМ-сигнала:

u_T(t) =j= (УгоcosloV -H9(01, и принятой смеси сигнала и шума иг (/)-• = Л„ sin \uj„t + 9(01 + "ш(0-

На выходе ФД образуется напряжение разностной и суммарной частот

ифд(0~ sin (9 (|) - 9>)|-г

^sin[2to_o/+9(0 + '9(0l + «m (t).

После прохождения через ФНЧ второе слагаемое отфильтровывается, а первое будет создавать входное управляющее напряжение УГ в правильном направлении при условии,

что |9 (t) — 8* (01 < л. Следовательно, данная система будет отслеживать мгновенную фазу принимаемого сигнала, так как выходное колебание УГ синхронизировано по фазе с принимаемым сигналом. Подобная система похожа на оптимальный демодулятор приемника ЧМ-сигналов, полу-

ченный в результате синтеза на основе теории нелинейной фильтрации (см. § 15.4). Однако отнести приемники ЧМ-сигнала с обратным управлением к классу оптимальных или квазиоптимальных систем пока нет достаточно строгих теоретических обоснований.

§ 15.7. Приемники однополосных сигналов

В § 15.2, 15.4 рассматривались приемники двухполосных AM- и ЧМ-сигнаЛов, где полезная информация содержится как в верхней, так и в нижней боковых полосах сигналов. В целях экономии мощности передатчика и уменьшения полосы частот излучаемого сигнала, что особенно важно в многоканальных радиолиниях связи и телеметрии, ограничиваются излучением одной боковой полосы (ОБП) частот (рис. 15.22). Напряжение одной верхней боковой частоты этого сигнала u₆ m_AAJ2 X xcos((o,. il)t представляет собой гармоническое колебание. Амплитудное детектирование подобного колебания даст постоянное напряжение, пропорциональное т_АА₀/2, частотное детектирование— также постоянное напряжение, пропорциональное частоте Q. На выходе же детекторов необходимо иметь переменные напряжения с частотой сообщения П. Следовательно, детектировать сигнал только одной боковой полосы частот нельзя, а нужно передавать или создавать искусственно в приемнике несущую частоту <о,.. Поэтому приемники сигналов с ОБП в соответствии с характером излучаемого сигнала могут быть двух типов: 1) с восстановлением в приемнике несущей частоты 10₍. из не полностью подавленного колебания этой частоты в передатчике (см. рис. 15.22) или передачей специального «пилот-сигнала» ш_йс, расстройка которого по отношению к частоте со_с является строго постоянной; 2) с воспроизведением в приемнике несущей частоты со_с без

передачи «пилот-сигнала» или сигна л а на несущей частоте.

Таким образом, в обоих случая: для осуществления операции детек тирования в приемнике требуете; опорный сигнал с несущей частоте!

"оп = Uо cos (со_с/ + Ч?о)-

Если к амплитудному детектор! подвести сумму напряжений опорной сигнала и верхней боковой полое! принятого сигнала:

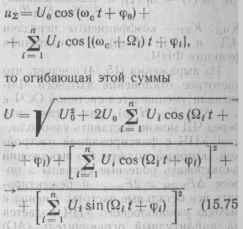
При большой амплитуде опорной сигнала по сравнению с принятьи (U₀ > Vi) квадратный корень мож но представить степенным рядом i пренебречь членами высших поряд ков, что приведет выражение (15.75 iK виду . :гк

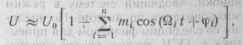
где т-. — Ui/U_u — коэффициент AM Эта огибающая обычного АМ-ко лебания и будет воспроизведена ам плитудным детектором, на выходе ко торого получается сумма постоян ной составляющей и переменных на пряжений с частотами Q_{.